14.7 等边三角形 课件(21张PPT)
文档属性
| 名称 | 14.7 等边三角形 课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 15:12:47 | ||
图片预览







文档简介
(共21张PPT)
《等边三角形》
名称
图
形
性
质
判
定
等
腰
三
角
形
A
B
C
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
知识回顾
你发现了什么?
这就是今天我们要学的
观察下列图片,你有
什么印象?
等边三角形:
(正三角形)
三条边都相等的三角形.
等边三角形是特殊的等腰三角形.
学习园地
1、定义:
2、等腰三角形与等边三角形的关系:
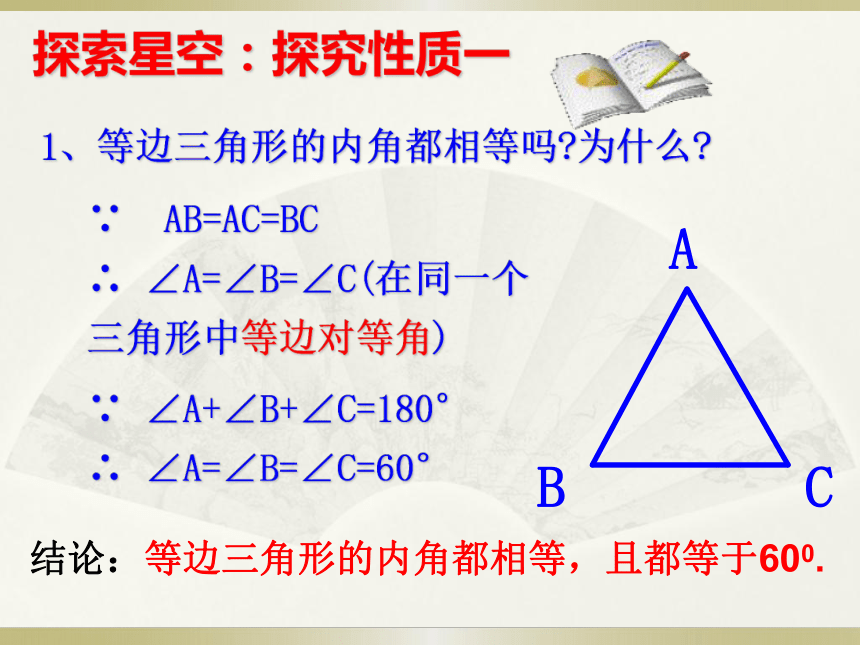
1、等边三角形的内角都相等吗 为什么
∵
AB=AC=BC
∴
∠A=∠B=∠C(在同一个三角形中等边对等角)
∵
∠A+∠B+∠C=180°
∴
∠A=∠B=∠C=60°
探索星空:探究性质一
结论:等边三角形的内角都相等,且都等于600.
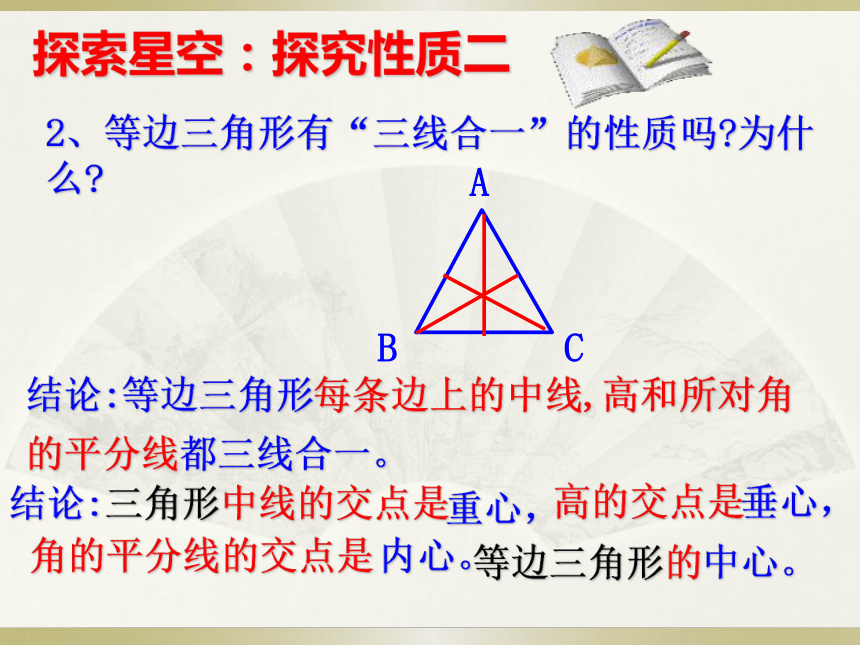
2、等边三角形有“三线合一”的性质吗 为什么
结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
探索星空:探究性质二
结论:三角形中线的交点是
等边三角形的中心。
角的平分线的交点是
高的交点是
内心。
垂心,
重心,
3、①等边三角形是轴对称图形吗 有几条对称轴
探索星空:探究性质三
结论:等边三角形是轴对称图形,它有三条对称轴(三边的中垂线).
3、
②等边三角形是旋转对称图形和中心对称图形吗 若是,它的旋转中心是什么?旋转角分别是多少度
探索星空:探究性质三
.O
结论:等边三角形是旋转对称图形,它的中心是旋转中心,旋转角是1200或2400.
等边三角形的性质
2.等边三角形的内角都相等,且等
于60°。
3.等边三角形各边上中线,高和
所对角的平分线都三线一。
4.等边三角形是轴对称图形,有
三条对称轴;也是旋转对称图形。
1.三条边相等。
∵
∠A=∠B=∠C(已知)
∴
AB=AC=BC
(在同一个三角形中等角对等边)
探索星空:探究判定一
1、三个内角都相等的三角形是等边三角形吗
∴
△ABC是等边三角形
。
判定1:三个内角都相等的三角形是等边三角形.
(1)腰与底边相等的等腰三角形是等边三角形。
探索星空:探究判定二
2、讨论:两边相等的三角形,满足怎样的条件就能成为等边三角形?
∴
△ABC是等边三角形
。
判定2:腰与底边相等的等腰三角形是等边三角形.
∵
AB=AB,AB=BC(已知)
∴
AB=AC=BC
(等量代换)
(2)有一个内角等于60°的等腰
三角形是等边三角形。
探索星空:探究判定三
(i)当顶角为60°时,
两个底角各为60°.
(ii)当底角为60°时,
顶角为60°.
判定3:有一个内角等于60°的等
腰三角形是等边三角形.
等边三角形的判定方法:
1.三边相等的三角形是等边三角形。
2.三个内角都相等的三角形是等边三角形。
4.有一个内角等于60°的等腰三角形是等边三角形。
3.腰与底边相等的三角形是等边三角形。
1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.
4.等边三角形的对称轴的交点叫__
_.
等边三角形绕中心至少旋转___度.才能和原来的三角形重合.
等边
60
3
中心
120
例1:如图,等边
ABC,以下三种方法分别得到的
ADE都是等边三角形吗?为什么?
(1)在边AB,AC,分别截取AD=AE。
(2)∠ADE=60°,D,E分
别在边AB,AC上。
(3)过边AB上D点,作
DE∥BC,交
AC于E点。
A
B
C
D
E
△
△
例2:如图,我校课外兴趣小组在一次测量活动中,测得∠APB=60°,AP=BP=200m,他们便知道池塘最长处是多少。猜猜他们得出结论是多少,请验证你的猜想。
名称
图
形
性
质
等
边
三
角
形
等边三角形的性质:
三个角都相等,且都等于60°
三线合一
三条边都相等
轴对称图形,有三条对称轴
(中心)
名称
图
形
判
定
等
边
三
角
形
等边三角形的判定:
三个角都相等的三角形
三条边都相等的三角形
有一个角等于60°的等腰三角形
腰与底边相等的等腰三角形
自主实践温顾所学
作业:
教材P114:1、2、3题
课后作业:练习册14.7
反馈练习:等边三角形ABC的周长等于12㎝,
求:(1)各边的长;
(2)各角的度数。
《等边三角形》
名称
图
形
性
质
判
定
等
腰
三
角
形
A
B
C
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
知识回顾
你发现了什么?
这就是今天我们要学的
观察下列图片,你有
什么印象?
等边三角形:
(正三角形)
三条边都相等的三角形.
等边三角形是特殊的等腰三角形.
学习园地
1、定义:
2、等腰三角形与等边三角形的关系:
1、等边三角形的内角都相等吗 为什么
∵
AB=AC=BC
∴
∠A=∠B=∠C(在同一个三角形中等边对等角)
∵
∠A+∠B+∠C=180°
∴
∠A=∠B=∠C=60°
探索星空:探究性质一
结论:等边三角形的内角都相等,且都等于600.
2、等边三角形有“三线合一”的性质吗 为什么
结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
探索星空:探究性质二
结论:三角形中线的交点是
等边三角形的中心。
角的平分线的交点是
高的交点是
内心。
垂心,
重心,
3、①等边三角形是轴对称图形吗 有几条对称轴
探索星空:探究性质三
结论:等边三角形是轴对称图形,它有三条对称轴(三边的中垂线).
3、
②等边三角形是旋转对称图形和中心对称图形吗 若是,它的旋转中心是什么?旋转角分别是多少度
探索星空:探究性质三
.O
结论:等边三角形是旋转对称图形,它的中心是旋转中心,旋转角是1200或2400.
等边三角形的性质
2.等边三角形的内角都相等,且等
于60°。
3.等边三角形各边上中线,高和
所对角的平分线都三线一。
4.等边三角形是轴对称图形,有
三条对称轴;也是旋转对称图形。
1.三条边相等。
∵
∠A=∠B=∠C(已知)
∴
AB=AC=BC
(在同一个三角形中等角对等边)
探索星空:探究判定一
1、三个内角都相等的三角形是等边三角形吗
∴
△ABC是等边三角形
。
判定1:三个内角都相等的三角形是等边三角形.
(1)腰与底边相等的等腰三角形是等边三角形。
探索星空:探究判定二
2、讨论:两边相等的三角形,满足怎样的条件就能成为等边三角形?
∴
△ABC是等边三角形
。
判定2:腰与底边相等的等腰三角形是等边三角形.
∵
AB=AB,AB=BC(已知)
∴
AB=AC=BC
(等量代换)
(2)有一个内角等于60°的等腰
三角形是等边三角形。
探索星空:探究判定三
(i)当顶角为60°时,
两个底角各为60°.
(ii)当底角为60°时,
顶角为60°.
判定3:有一个内角等于60°的等
腰三角形是等边三角形.
等边三角形的判定方法:
1.三边相等的三角形是等边三角形。
2.三个内角都相等的三角形是等边三角形。
4.有一个内角等于60°的等腰三角形是等边三角形。
3.腰与底边相等的三角形是等边三角形。
1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.
4.等边三角形的对称轴的交点叫__
_.
等边三角形绕中心至少旋转___度.才能和原来的三角形重合.
等边
60
3
中心
120
例1:如图,等边
ABC,以下三种方法分别得到的
ADE都是等边三角形吗?为什么?
(1)在边AB,AC,分别截取AD=AE。
(2)∠ADE=60°,D,E分
别在边AB,AC上。
(3)过边AB上D点,作
DE∥BC,交
AC于E点。
A
B
C
D
E
△
△
例2:如图,我校课外兴趣小组在一次测量活动中,测得∠APB=60°,AP=BP=200m,他们便知道池塘最长处是多少。猜猜他们得出结论是多少,请验证你的猜想。
名称
图
形
性
质
等
边
三
角
形
等边三角形的性质:
三个角都相等,且都等于60°
三线合一
三条边都相等
轴对称图形,有三条对称轴
(中心)
名称
图
形
判
定
等
边
三
角
形
等边三角形的判定:
三个角都相等的三角形
三条边都相等的三角形
有一个角等于60°的等腰三角形
腰与底边相等的等腰三角形
自主实践温顾所学
作业:
教材P114:1、2、3题
课后作业:练习册14.7
反馈练习:等边三角形ABC的周长等于12㎝,
求:(1)各边的长;
(2)各角的度数。
