北师大版九年级数学下册第一章:1.5 三角函数的应用 提高培优讲义(含答案)
文档属性
| 名称 | 北师大版九年级数学下册第一章:1.5 三角函数的应用 提高培优讲义(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 00:00:00 | ||
图片预览




文档简介
北师大版九年级数学下册第一章 直角三角形的边角关系 提高培优讲义:
三角函数的应用
模块一 解三角形
1.解直角三角形
在直角三角形中,除直角外,一共有5个元素,即3条边和2个锐角,由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.
2.直角三角形的边角关系
(1)三边之间的关系:.(勾股定理)
(2)锐角之间的关系:
(3)边角之间的关系:,,.
3.解直角三角形的四种基本类型
已知条件 解法类型
一条边和一个锐角 斜边c和锐角 ,,
直角边a和锐角 ,,
两条边 两条直角边a和b ,,
斜边c和直角边a ,,
4.解一般三角形
(1)利用三角函数值构造直角三角形,然后解直角三角形.
(2)把角度进行转移,利用常见的倒角模型和平行线进行角度转移.
模块二 解三角形的应用
1.相关概念
(1)仰角与俯角:在视线与水平线所成的角中,视线在水平线上方的叫做仰角,在水平线下方的叫做俯角.如图1.
(2)坡角与坡度:坡面的垂直高度h和水平宽度l的比叫做坡度(或叫做坡比),用字母表示为,坡面与水平面的夹角记作,叫做坡角,则.坡度越大,坡面就越陡.如图2.
(3)方向角(或方位角):方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达为北(南)偏东(西)××度.如图3.
图1 图2 图3
2.解直角三角形应用题的解题步骤及应注意的问题:
(1)分析题意,根据已知条件画出它的平面或截面示意图,分清仰角、俯角、坡角、坡度、水平距离、垂直距离等概念的意义;
(2)找出要求解的直角三角形.有些图形虽然不是直角三角形,但可添加适当的辅助线,把它们分割成一些直角三角形和矩形(包括正方形);
(3)根据已知条件,选择合适的边角关系式解直角三角形;
(4)按照题目中已知数据的精确度进行近似计算,检验是否符合实际,并按题目要求的精确度取近似值,注明单位.
模块三 例题讲解
SHAPE \* MERGEFORMAT
在中,.
(1)若,,则________,________,________;
(2)若,,则________,________;
(3)若,,则________,________.
【解析】(1),3,;(2),;(3);.
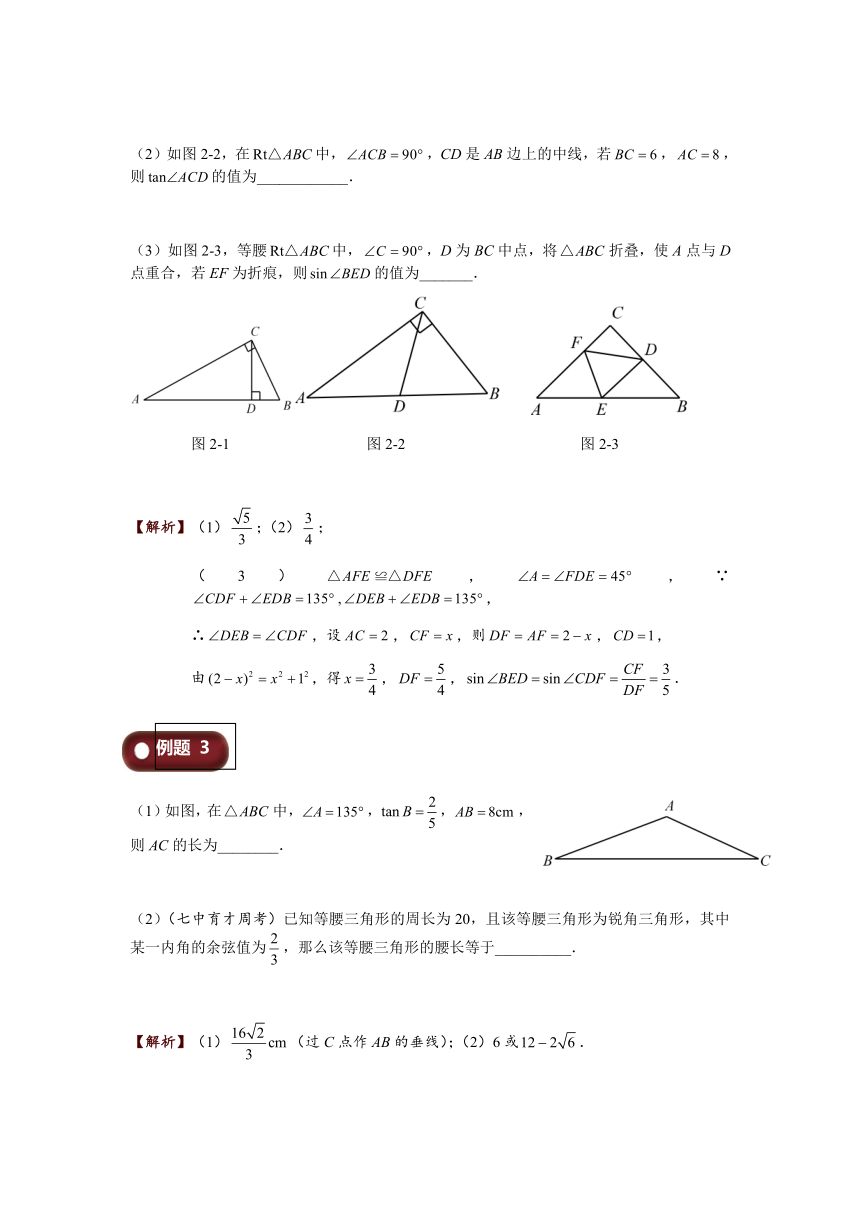
(1)如图2-1,在中,,于点D,,,则____________.
(2)如图2-2,在中,,CD是AB边上的中线,若,,则的值为____________.
(3)如图2-3,等腰中,,D为BC中点,将折叠,使A点与D点重合,若EF为折痕,则的值为_______.
图2-1 图2-2 图2-3
【解析】(1);(2);
(3),,∵,,
∴,设,,则,,
由,得,,.
(1)如图,在中,,,,则AC的长为________.
(2)(七中育才周考)已知等腰三角形的周长为20,且该等腰三角形为锐角三角形,其中某一内角的余弦值为,那么该等腰三角形的腰长等于__________.
【解析】(1)(过C点作AB的垂线);(2)6或.
如图,已知在中,,,D为边BC的中点,E为边BC的延长线上一点,且,连接AE.
(1)求线段DE的长;
(2)求的正切值.
【解析】(1)如图,连接AD,
∵,D为BC的中点,∴,∴,
∵,,∴,
∴,由勾股定理得:,∴,,
∵,∴,∴;
(2)过C作于M,则,
在中,由勾股定理得;,
∵由勾股定理得;,
∴,
解得:,∴,
∴的正切值是.
如图,在中,CD是AB边上的中线,已知,,,
(1)求面积;(2)求CD的长;(3)求的值.
【解析】(1)作于H,在中,
∵,,∴,
设,,根据勾股定理得,
∴,∴,,
在中,,∴,
∴,∴;
(2)作于F,∴,
∵,∴,∴,
∴,∴;
(3)作于E,∵,∴,
∴,∴.
如图,等腰中,,,,点D在边AC上,且BD平分.
(1)求证:;
(2)求的值.
【解析】(1)∵等腰中,,,∴,
∵BD平分,∴,
∵,,∴;
(2)∵,∴,
∵,∴,设,则有,
∵,∴,即,整理得:,
解得:,(负值,舍去),则;
过B作,交AC于点E,
∵,∴E为CD中点,即,
在中,,
在中,,
则.
如图,一座商场大楼的顶部竖直立有一个矩形广告牌,小红同学在地面上选择了在一条直线上的三个点A(A为楼底)、D、E,她在D处测得广告牌顶端C的仰角为,在E处测得商场大楼楼顶B的仰角为,米.已知,广告牌的高度米,求这座商场大楼的高度AB(,,小红的身高不计,结果保留整数).
【解析】设AB为x米.
依题意,在中,
∴,
∴,.
在中,,
∴
∴,
∴,
解得,∴.
“五?一”期间,小亮与家人到某旅游风景区登山,他们沿着坡度为的山坡AB向上走了1300米,到达缆车站B处,乘坐缆车到达山顶C处,已知点A、B、C、D在同一平面内,从山脚A处看山顶C处的仰角为,缆车行驶路线BC与水平面的夹角为,求山高CD.(结果精确到0.1米,,)(注:坡度是指坡面的铅直高度与水平宽度的比)
【解析】过B作于E,于F,
则,,,
所以四边形BFDE是矩形,所以,,
∵沿着坡度为的山坡AB向上走了1300米,到达缆车站B处,
∴米,米,
∵,∴,
∵在中,,∴,
∴,解得:米,
∴米,
∴米≈789.2米.
模块四 复习巩固
(1)如图1-1,在菱形ABCD中,,,,则BD的长为______,的值为_______.
(2)如图1-2,在梯形ABCD中,,,,,则_______.
图1-1 图1-2
【解析】(1),;(2).
(1)如图2-1,在等腰中,,,D是AC边上一点,若,则AD的长为____________.
(2)如图2-2,是等腰直角三角形,,过BC的中点D作,垂足为E,连接CE,则的值为____________.
图2-1 图2-2
【解析】(1)作于点E,则,且,
又可得,从而.
(2)过点E作,F为垂足.,也是等腰直角三角形.
设,则,∴,,.
如图,点E是矩形ABCD中CD边上一点,沿BE折叠为,点F落在AD上,
(1)求证:;
(2)若,求的值.
【解析】(1)略;
(2)由,得,
故.
某校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动.如图,她在山坡坡脚A出测得这座楼房的楼顶B点的仰角为,沿山坡往上走到C处再测得B点的仰角为.已知,此山坡的坡比,且O、A、D在同一条直线上.求:(1)楼房OB的高度;(2)小红在山坡上走过的距离AC.(计算过程和结果均不取近似值)
【解析】(1)在中,,.
∵,∴.
(2)如图,过点C作于E,于H.
则,.
根据题意,知,可设,.
在中,,
∴,即.
∴.解得.
在中,
∵,∴.
∴.
答:高楼OB的高度为,小红在山坡上走过的距离AC为m.
如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:,,)
【解析】(1)如图,过点E作,垂足为M.设AB为x.
中,,
∴,
∴,
在中,,
,
,则,解得:.
即教学楼的高20m.
(2)由(1)可得.
在中,.∴,
即A、E之间的距离约为48m.
例题 1
例题 2
例题 3
例题 4
例题 5
例题 6
例题 7
例题 8
演练 1
演练 2
演练 3
演练 4
演练 5
