沪科版九年级数学下册:24.1.3 中心对称图形 课件 (共25张PPT)
文档属性
| 名称 | 沪科版九年级数学下册:24.1.3 中心对称图形 课件 (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 00:00:00 | ||
图片预览







文档简介
课件25张PPT。第二十四章
圆九年级数学沪科版·下册24.1.3中心对称图形教学目标1.掌握两点关于原点对称时,横纵坐标的关系.(难点)
2.会在平面直角坐标系内作关于原点对称的图形.(重点)
3.利用旋转、轴对称或平移进行简单的图案设计.(重点).
复习导入 下列各点分别在平面直角坐标系的什么位置上?A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
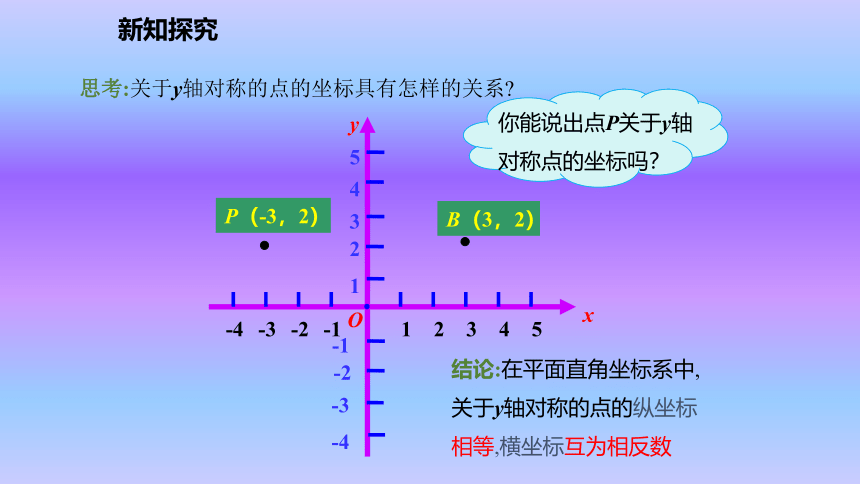
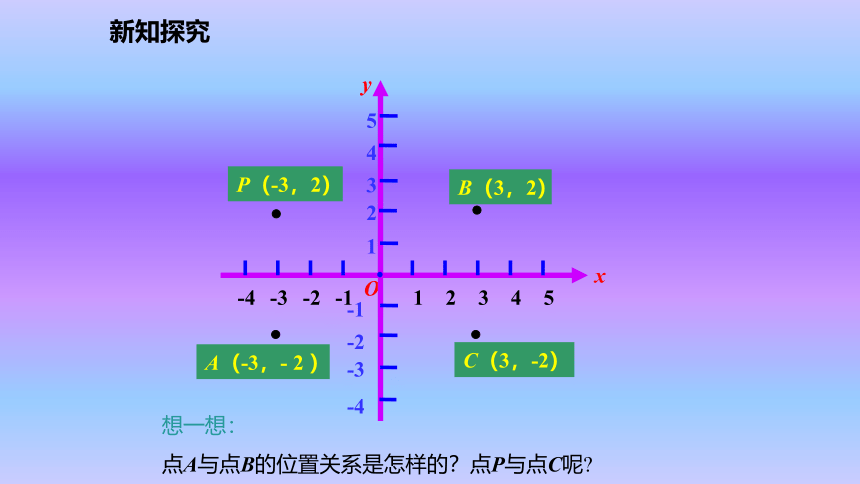
F(2,-3)第一象限第三象限第二象限第四象限y轴上x轴上新知探究问题:2016年里约热内卢奥运会会徽是三人牵手相连的标志,以代表巴西的著名景点“面包山”作为图形的基础,融合充满激情的卡里奥克舞,并且呼应了巴西国旗的绿黄蓝三色.说一说图案中的奥运五环可以通过其中一个圆怎样变化而得到?新知探究互动探究123OxP(-3,2)A(-3,- 2 ) y思考:关于x轴对称的点的坐标具有怎样的关系?结论:在平面直角坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数.·新知探究123OxB(3,2)P(-3,2)y 思考:关于y轴对称的点的坐标具有怎样的关系?结论:在平面直角坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数·新知探究123OxB(3,2)C(3,-2)P(-3,2)A(-3,- 2 ) 想一想:
点A与点B的位置关系是怎样的?点P与点C呢?y·新知探究简记为:“关于谁,谁不变,关于原点都改变”.点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a, b).归纳总结新知探究例1 填空:
(1)在平面直角坐标系中,点P(2,-3)关于原点对称的点P′的坐标是________.
(2)点P(2,n)与点Q(m,-3)关于原点对称,则(m+n)2020=________.
(3)点M(3,-5)绕原点旋转180°后到达的位置是________.解析:(1)因为点P(2,-3)与点P′关于原点对称,所以点P′的坐标是P′(-2,3).
(2)因为点P(2,n)与点Q(m,-3)关于原点对称,所以m=-2,n=3,则(m+n)2020=(-2+3)2020=1.
(3)因为点M(3,-5)绕原点旋转180°后到达的位置与原来的点关于原点对称,所以到达的位置是(-3,5).(-2,3)1(-3,5)新知探究例2 如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.Oxy·ACBA′C′B′解:△ABC的三个顶点
A(-4,1),B(-1, -1),C(-3,2)A′(4,-1),B′(1,1),C′(3,-2)关于原点的对称点分别为依次连接A ′B ′ ,B ′ C ′ ,C ′ A ′ ,就可得到与△ABC关于原点对称的△ A′B′ C ′ .新知探究方法归纳 (1)写出图形顶点坐标;
(2)写出图形顶点关于原点的对称点的坐标;
(3)描点;
(4)顺次连接;
(5)下结论.作关于原点对称的图形的步骤:新知探究试说出构成下列图形的基本图形.基本图形(1)(2)(3)(4)想一想:看成轴对称时基本图形是什么?观察与思考新知探究基本图案图案的形成过程分析图案的形成过程
新知探究基本图案图案的形成过程分析图案的形成过程
新知探究 图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案.新知探究 例2 下面花边中的图案以正方形为基础,由圆弧、圆或线段构成.仿照例图,请你为班级的板报设计一条花边.要求:(1)只要画出组成花边的一个图案;(2)以所给的正方形为基础,用圆弧、圆或线段画出;(3)图案应有美感. 典例精析新知探究参考图案新知探究你能找出图案中的全等图形吗?这幅图案可看成是怎样制作的呢?
图片欣赏新知探究运动美新知探究运动美新知探究课堂小结旋转的应用特征P (x,y)关于原点的对称点为P′(-x,-y).作图作出关于原点对称的图形,先求出对称点的坐标再描点画图.平面直角坐标系内的旋转变换动态图形的操作与图案设计分析图案设计分清基本图形知道形成过程设计方法利用图形变换轴对称平 移旋 转课堂小测1.下列各点中哪两个点关于原点O对称?
A(-5,0) B(0,2) C(2,-1) D(2,0)
E(0,5) F(-2,1) G(-2,-1)
2.写出下列各点关于原点的对称点的坐标.
A(3,1) B(-2,3) C(-1,-2) D(2,-3)
A(-3,-1) B(2,-3) C(1,2) D(-2,3)3.若点A(m,-2),B(1,n)关于原点对称,则m=_____,n=_____ .-12课堂小测4.在如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为________.①与②①与③课堂小测5.已知a<0,则点P(-a2,-a+1)关于原点的对称点P′在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限 解析:∵点P(-a2,-a+1)关于原点的对称点P′的坐标为(a2,a-1),
∵a<0,
∴a2>0,a-1<0,
∴点P′在第四象限.D
2.会在平面直角坐标系内作关于原点对称的图形.(重点)
3.利用旋转、轴对称或平移进行简单的图案设计.(重点).
复习导入 下列各点分别在平面直角坐标系的什么位置上?A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)第一象限第三象限第二象限第四象限y轴上x轴上新知探究问题:2016年里约热内卢奥运会会徽是三人牵手相连的标志,以代表巴西的著名景点“面包山”作为图形的基础,融合充满激情的卡里奥克舞,并且呼应了巴西国旗的绿黄蓝三色.说一说图案中的奥运五环可以通过其中一个圆怎样变化而得到?新知探究互动探究123OxP(-3,2)A(-3,- 2 ) y思考:关于x轴对称的点的坐标具有怎样的关系?结论:在平面直角坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数.·新知探究123OxB(3,2)P(-3,2)y 思考:关于y轴对称的点的坐标具有怎样的关系?结论:在平面直角坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数·新知探究123OxB(3,2)C(3,-2)P(-3,2)A(-3,- 2 ) 想一想:
点A与点B的位置关系是怎样的?点P与点C呢?y·新知探究简记为:“关于谁,谁不变,关于原点都改变”.点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a, b).归纳总结新知探究例1 填空:
(1)在平面直角坐标系中,点P(2,-3)关于原点对称的点P′的坐标是________.
(2)点P(2,n)与点Q(m,-3)关于原点对称,则(m+n)2020=________.
(3)点M(3,-5)绕原点旋转180°后到达的位置是________.解析:(1)因为点P(2,-3)与点P′关于原点对称,所以点P′的坐标是P′(-2,3).
(2)因为点P(2,n)与点Q(m,-3)关于原点对称,所以m=-2,n=3,则(m+n)2020=(-2+3)2020=1.
(3)因为点M(3,-5)绕原点旋转180°后到达的位置与原来的点关于原点对称,所以到达的位置是(-3,5).(-2,3)1(-3,5)新知探究例2 如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.Oxy·ACBA′C′B′解:△ABC的三个顶点
A(-4,1),B(-1, -1),C(-3,2)A′(4,-1),B′(1,1),C′(3,-2)关于原点的对称点分别为依次连接A ′B ′ ,B ′ C ′ ,C ′ A ′ ,就可得到与△ABC关于原点对称的△ A′B′ C ′ .新知探究方法归纳 (1)写出图形顶点坐标;
(2)写出图形顶点关于原点的对称点的坐标;
(3)描点;
(4)顺次连接;
(5)下结论.作关于原点对称的图形的步骤:新知探究试说出构成下列图形的基本图形.基本图形(1)(2)(3)(4)想一想:看成轴对称时基本图形是什么?观察与思考新知探究基本图案图案的形成过程分析图案的形成过程
新知探究基本图案图案的形成过程分析图案的形成过程
新知探究 图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案.新知探究 例2 下面花边中的图案以正方形为基础,由圆弧、圆或线段构成.仿照例图,请你为班级的板报设计一条花边.要求:(1)只要画出组成花边的一个图案;(2)以所给的正方形为基础,用圆弧、圆或线段画出;(3)图案应有美感. 典例精析新知探究参考图案新知探究你能找出图案中的全等图形吗?这幅图案可看成是怎样制作的呢?
图片欣赏新知探究运动美新知探究运动美新知探究课堂小结旋转的应用特征P (x,y)关于原点的对称点为P′(-x,-y).作图作出关于原点对称的图形,先求出对称点的坐标再描点画图.平面直角坐标系内的旋转变换动态图形的操作与图案设计分析图案设计分清基本图形知道形成过程设计方法利用图形变换轴对称平 移旋 转课堂小测1.下列各点中哪两个点关于原点O对称?
A(-5,0) B(0,2) C(2,-1) D(2,0)
E(0,5) F(-2,1) G(-2,-1)
2.写出下列各点关于原点的对称点的坐标.
A(3,1) B(-2,3) C(-1,-2) D(2,-3)
A(-3,-1) B(2,-3) C(1,2) D(-2,3)3.若点A(m,-2),B(1,n)关于原点对称,则m=_____,n=_____ .-12课堂小测4.在如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为________.①与②①与③课堂小测5.已知a<0,则点P(-a2,-a+1)关于原点的对称点P′在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限 解析:∵点P(-a2,-a+1)关于原点的对称点P′的坐标为(a2,a-1),
∵a<0,
∴a2>0,a-1<0,
∴点P′在第四象限.D
