3.1.1倾斜角与斜率(共34张PPT)
文档属性
| 名称 | 3.1.1倾斜角与斜率(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 22:36:57 | ||
图片预览



文档简介
(共34张PPT)
我们怎么确定这些直线的位置?
我们怎么确定这些直线的位置?
3.1.1 倾斜角与斜率
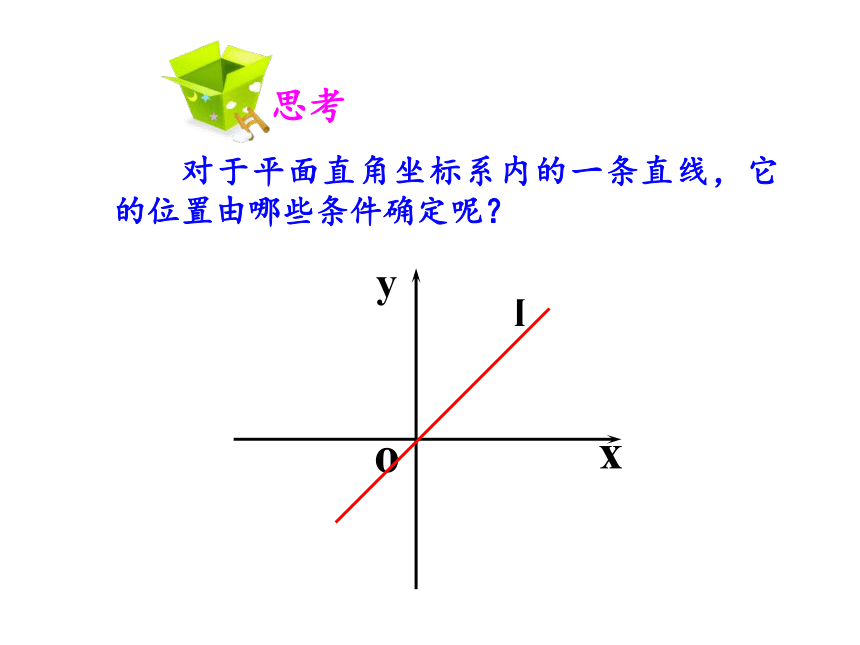
对于平面直角坐标系内的一条直线,它的位置由哪些条件确定呢?
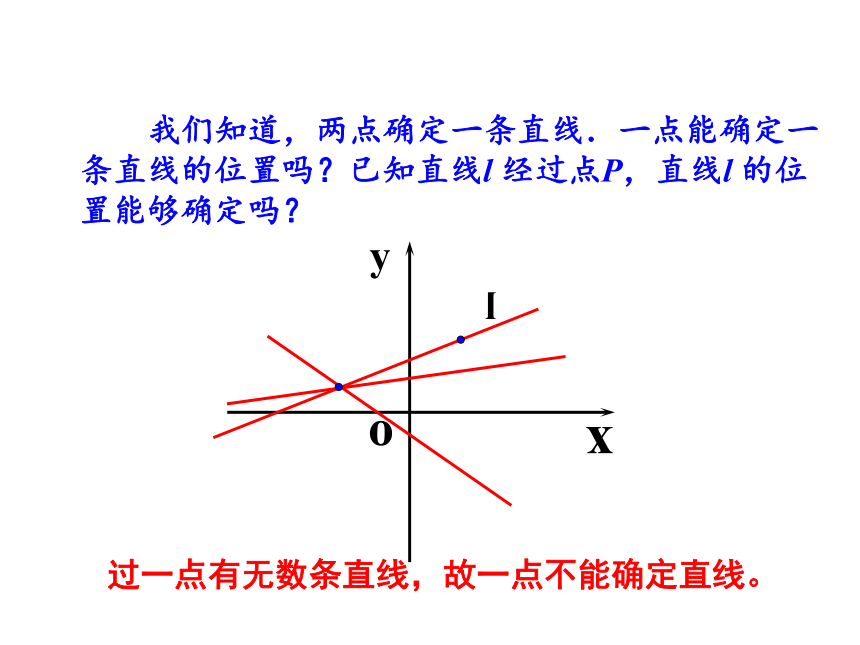
我们知道,两点确定一条直线.一点能确定一条直线的位置吗?已知直线l 经过点P,直线l 的位置能够确定吗?
过一点有无数条直线,故一点不能确定直线。
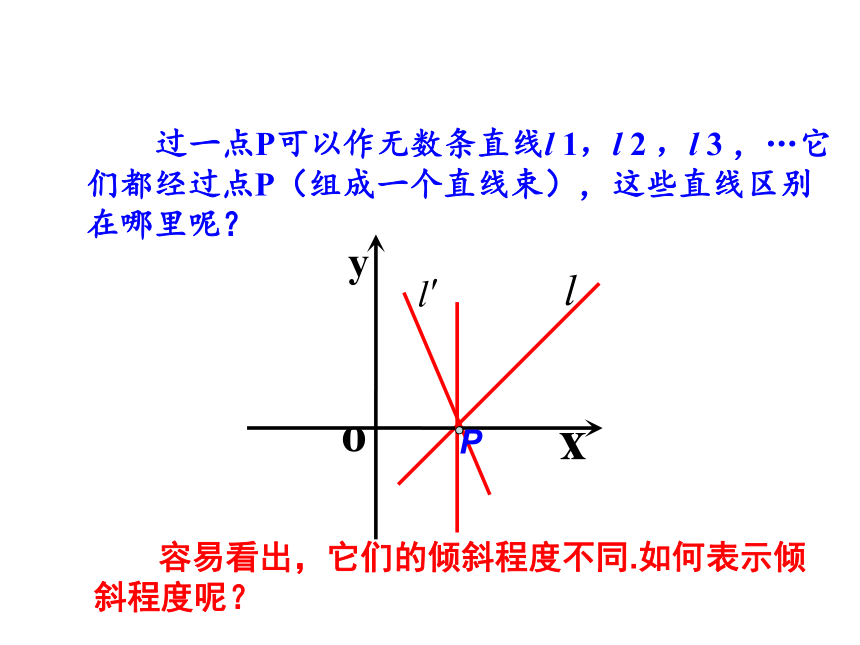
过一点P可以作无数条直线l 1,l 2 ,l 3 ,…它们都经过点P(组成一个直线束),这些直线区别在哪里呢?
容易看出,它们的倾斜程度不同.如何表示倾斜程度呢?
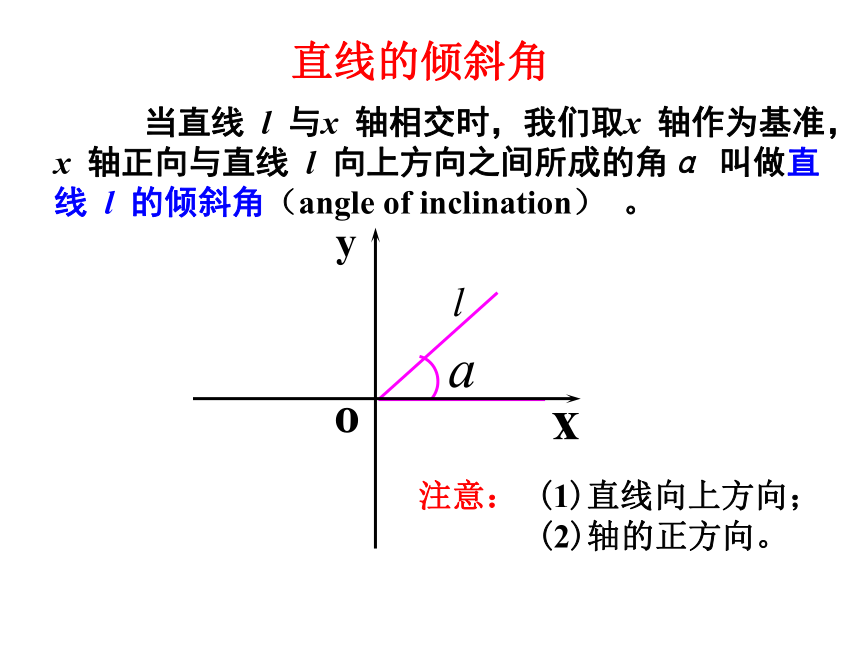
当直线 l 与x 轴相交时,我们取x 轴作为基准,x 轴正向与直线 l 向上方向之间所成的角α 叫做直线 l 的倾斜角(angle of inclination) 。
直线的倾斜角
注意: (1)直线向上方向;
(2)轴的正方向。
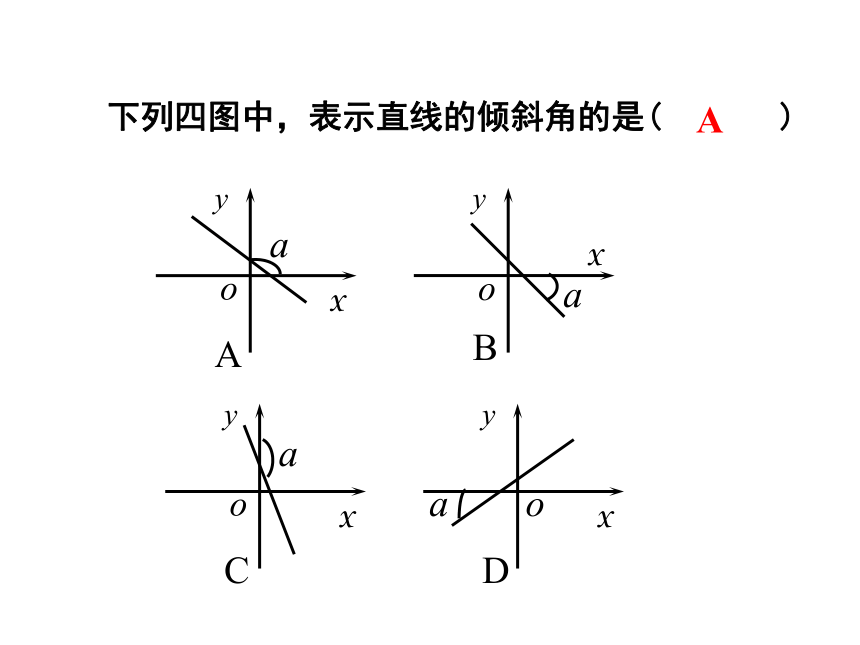
下列四图中,表示直线的倾斜角的是( )
A
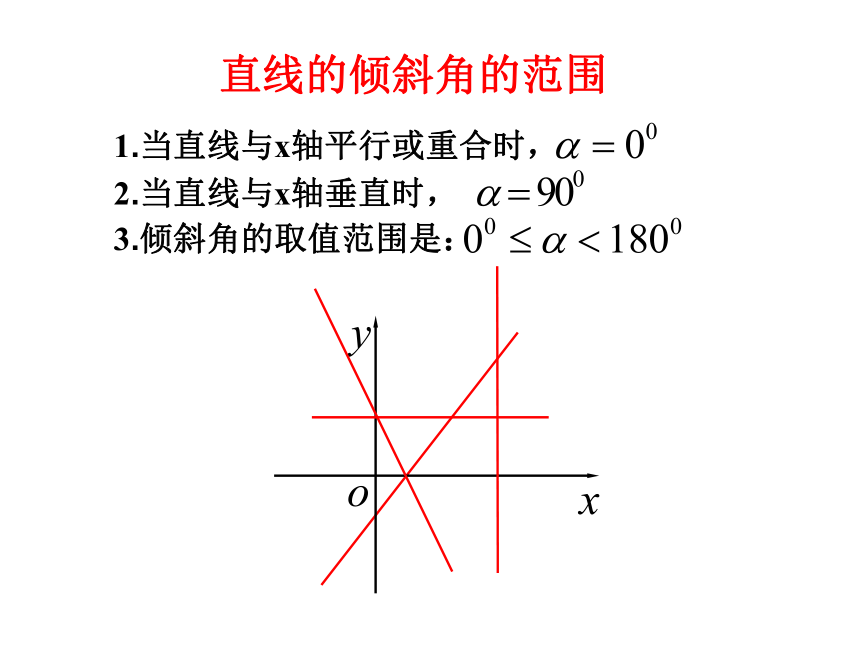
直线的倾斜角的范围
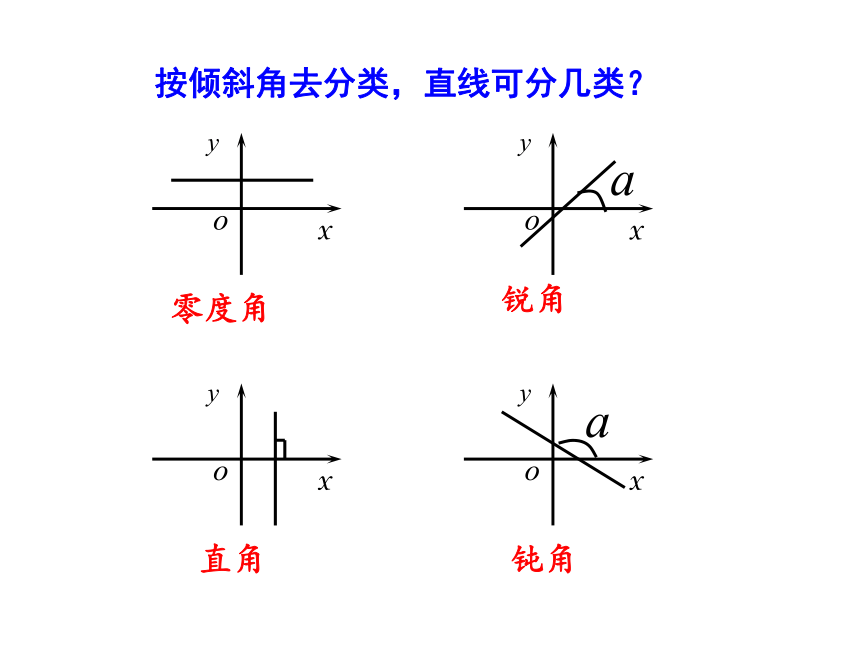
按倾斜角去分类,直线可分几类?
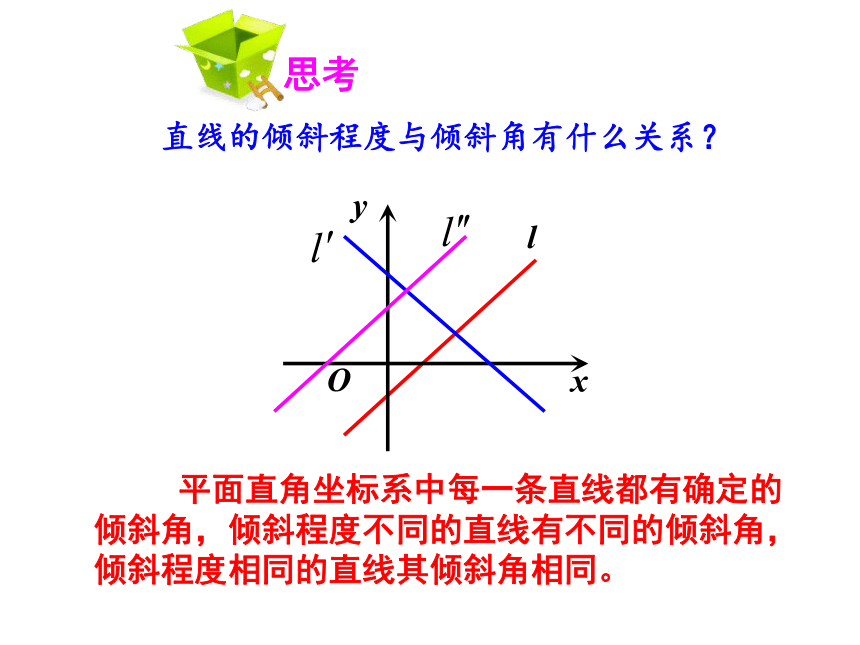
直线的倾斜程度与倾斜角有什么关系?
平面直角坐标系中每一条直线都有确定的倾斜角,倾斜程度不同的直线有不同的倾斜角,倾斜程度相同的直线其倾斜角相同。
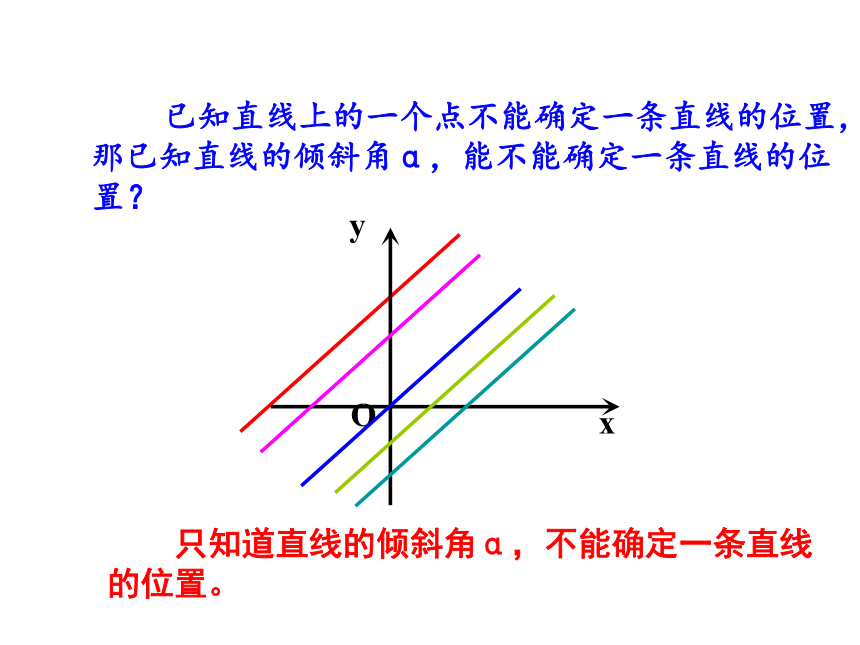
只知道直线的倾斜角α,不能确定一条直线的位置。
已知直线上的一个点不能确定一条直线的位置,那已知直线的倾斜角α,能不能确定一条直线的位置?
x
y
O
确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角, 二者缺一不可。
日常生活中,还有没有表示倾斜程度的量?
我们经常用“升高量与前进量的比”表示倾斜面的“坡度”(倾斜程度),即
一条直线的倾斜角α的正切值叫做这条直线的斜率(slope)。通常用小写字母k表示,即
如果使用“倾斜角”这个概念,那么这里的“坡度(比)”实际就是“倾斜角α的正切”.
直线的斜率
直线斜率的范围
x
y
O
倾斜角α为锐角,斜率k>0.
倾斜角α为钝角,斜率k<0.
倾斜角α为0°,斜率k=0.
倾斜角α为90°,无斜率。
斜率的计算
已知直线上两点的坐标,如何计算直线的斜率?
给定两点P1 ( x1 ,y1), P2 ( x2 ,y2), 并且x1 ≠x2,如何计算直线P1 P2的斜率k.
设直线P1 P2的倾斜角为α( α ≠90° ),当直线P1 P2的方向(即从P1指向P2的方向)向上时,过点P1作 x 轴的平行线,过点P2作 y 轴的平行线,两线相交于点 Q,于是点Q的坐标为( x2,y1 )。
当α 为锐角时,
当α为钝角时,
当直线 与 x轴平行或重合时,上述式子还成立吗?为什么?
成立,因为分子为0,分母不为0,K=0。
直线的斜率公式
与A、B两点的顺序无关。
(2)当直线与y轴平行或重合时,上述式子还成立吗?为什么?
不成立,因为分母为0。
因此,这条直线的斜率是-1,倾斜角是135°。
求经过点A(-2,0),B(-5,3)两点的直线的倾斜角和斜率。
解:直线AB的斜率
1、直线的倾斜角定义及其范围:
2、直线的斜率定义:
4、斜率公式:
1.若k≥0,则α的范围是______________。
若k<0,则α的范围是________________。
0 ° < α < 90 °
90 ° < α < 180 °
(1)直线的倾斜角为α,则直线的斜率为tan α。
(2)直线的斜率为tan β,则直线的倾斜角为β。
(3)所有的直线都有倾斜角,故所有的直线都有斜率。
2.判断正误:
×
×
×
3.求过下列两点的直线的斜率k及倾斜角α
① P1(-2,3),P2(-2,8);
② P1(5,-2),P2(-2,-2);
③ P1(-1,2),P2(3,-4);
①k不存在,α=900;
②k=0, α=0°;
③k=-3/2, α=π-arctan3/2。
4.已知直线的倾斜角α满足cosα=a/5,(|a|<5),求该直线的斜率。
(1)a=0,cosα=0,α=90°,k不存在。
(2)当a≠0时,∵|a|<5,α>=0且α>=π,
所以,当a=0时所求直线的斜率不存在;
当a≠0时所求直线的斜率为
5.关于直线的倾斜角和斜率,下列那些说法是正确的( )
A. 任一条直线都有倾斜角,也都有斜率
B. 直线的倾斜角越大,他的斜率越大
C. 平行于轴的直线的倾斜角是0或π
D. 两条直线的倾斜角相等,他们的斜率也相等
E. 直线斜率的范围是(-∞,+∞)
D,E
我们怎么确定这些直线的位置?
我们怎么确定这些直线的位置?
3.1.1 倾斜角与斜率
对于平面直角坐标系内的一条直线,它的位置由哪些条件确定呢?
我们知道,两点确定一条直线.一点能确定一条直线的位置吗?已知直线l 经过点P,直线l 的位置能够确定吗?
过一点有无数条直线,故一点不能确定直线。
过一点P可以作无数条直线l 1,l 2 ,l 3 ,…它们都经过点P(组成一个直线束),这些直线区别在哪里呢?
容易看出,它们的倾斜程度不同.如何表示倾斜程度呢?
当直线 l 与x 轴相交时,我们取x 轴作为基准,x 轴正向与直线 l 向上方向之间所成的角α 叫做直线 l 的倾斜角(angle of inclination) 。
直线的倾斜角
注意: (1)直线向上方向;
(2)轴的正方向。
下列四图中,表示直线的倾斜角的是( )
A
直线的倾斜角的范围
按倾斜角去分类,直线可分几类?
直线的倾斜程度与倾斜角有什么关系?
平面直角坐标系中每一条直线都有确定的倾斜角,倾斜程度不同的直线有不同的倾斜角,倾斜程度相同的直线其倾斜角相同。
只知道直线的倾斜角α,不能确定一条直线的位置。
已知直线上的一个点不能确定一条直线的位置,那已知直线的倾斜角α,能不能确定一条直线的位置?
x
y
O
确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角, 二者缺一不可。
日常生活中,还有没有表示倾斜程度的量?
我们经常用“升高量与前进量的比”表示倾斜面的“坡度”(倾斜程度),即
一条直线的倾斜角α的正切值叫做这条直线的斜率(slope)。通常用小写字母k表示,即
如果使用“倾斜角”这个概念,那么这里的“坡度(比)”实际就是“倾斜角α的正切”.
直线的斜率
直线斜率的范围
x
y
O
倾斜角α为锐角,斜率k>0.
倾斜角α为钝角,斜率k<0.
倾斜角α为0°,斜率k=0.
倾斜角α为90°,无斜率。
斜率的计算
已知直线上两点的坐标,如何计算直线的斜率?
给定两点P1 ( x1 ,y1), P2 ( x2 ,y2), 并且x1 ≠x2,如何计算直线P1 P2的斜率k.
设直线P1 P2的倾斜角为α( α ≠90° ),当直线P1 P2的方向(即从P1指向P2的方向)向上时,过点P1作 x 轴的平行线,过点P2作 y 轴的平行线,两线相交于点 Q,于是点Q的坐标为( x2,y1 )。
当α 为锐角时,
当α为钝角时,
当直线 与 x轴平行或重合时,上述式子还成立吗?为什么?
成立,因为分子为0,分母不为0,K=0。
直线的斜率公式
与A、B两点的顺序无关。
(2)当直线与y轴平行或重合时,上述式子还成立吗?为什么?
不成立,因为分母为0。
因此,这条直线的斜率是-1,倾斜角是135°。
求经过点A(-2,0),B(-5,3)两点的直线的倾斜角和斜率。
解:直线AB的斜率
1、直线的倾斜角定义及其范围:
2、直线的斜率定义:
4、斜率公式:
1.若k≥0,则α的范围是______________。
若k<0,则α的范围是________________。
0 ° < α < 90 °
90 ° < α < 180 °
(1)直线的倾斜角为α,则直线的斜率为tan α。
(2)直线的斜率为tan β,则直线的倾斜角为β。
(3)所有的直线都有倾斜角,故所有的直线都有斜率。
2.判断正误:
×
×
×
3.求过下列两点的直线的斜率k及倾斜角α
① P1(-2,3),P2(-2,8);
② P1(5,-2),P2(-2,-2);
③ P1(-1,2),P2(3,-4);
①k不存在,α=900;
②k=0, α=0°;
③k=-3/2, α=π-arctan3/2。
4.已知直线的倾斜角α满足cosα=a/5,(|a|<5),求该直线的斜率。
(1)a=0,cosα=0,α=90°,k不存在。
(2)当a≠0时,∵|a|<5,α>=0且α>=π,
所以,当a=0时所求直线的斜率不存在;
当a≠0时所求直线的斜率为
5.关于直线的倾斜角和斜率,下列那些说法是正确的( )
A. 任一条直线都有倾斜角,也都有斜率
B. 直线的倾斜角越大,他的斜率越大
C. 平行于轴的直线的倾斜角是0或π
D. 两条直线的倾斜角相等,他们的斜率也相等
E. 直线斜率的范围是(-∞,+∞)
D,E
