3.1.2两条直线平行与垂直的判定(共26张PPT)
文档属性
| 名称 | 3.1.2两条直线平行与垂直的判定(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 911.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 22:43:14 | ||
图片预览


文档简介
(共26张PPT)
3.1.2 两条直线平行与垂直的判定
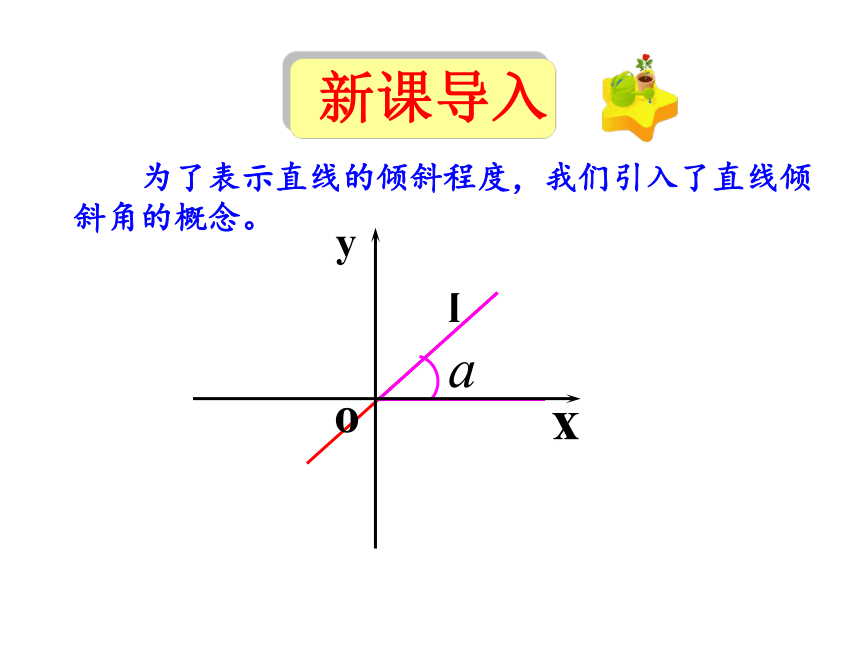
为了表示直线的倾斜程度,我们引入了直线倾斜角的概念。
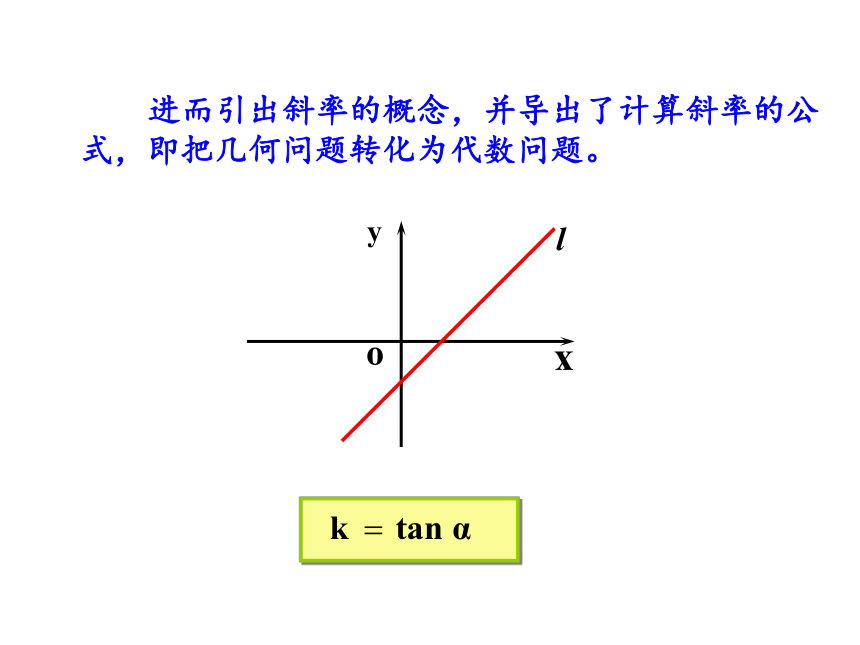
进而引出斜率的概念,并导出了计算斜率的公式,即把几何问题转化为代数问题。
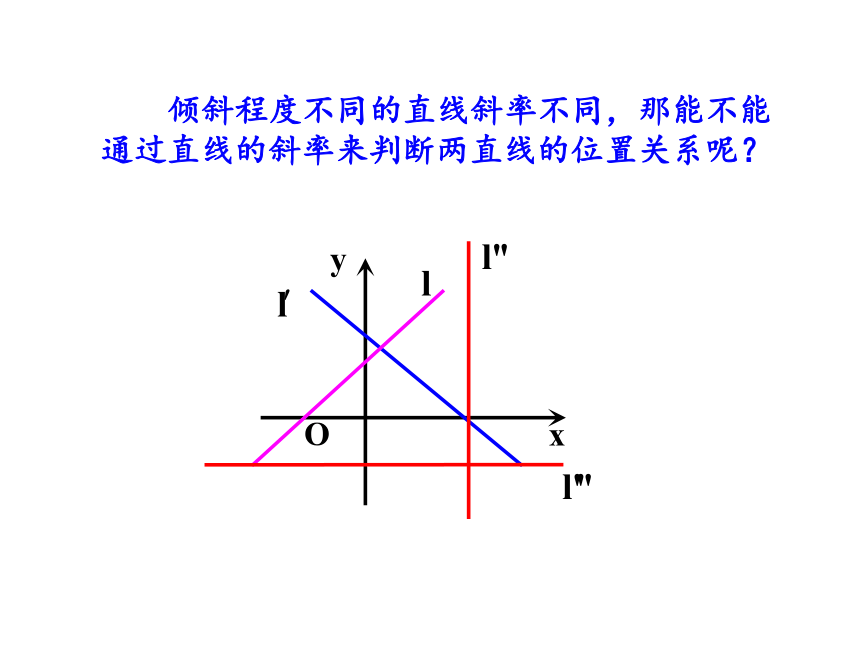
倾斜程度不同的直线斜率不同,那能不能通过直线的斜率来判断两直线的位置关系呢?
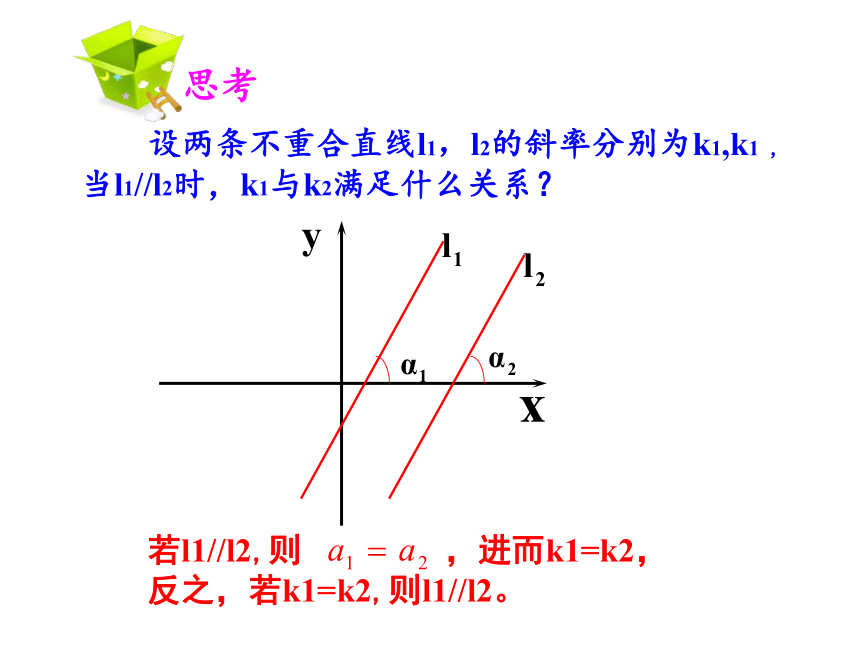
设两条不重合直线l1,l2的斜率分别为k1,k1 , 当l1//l2时,k1与k2满足什么关系?
若l1//l2,则 ,进而k1=k2,反之,若k1=k2,则l1//l2。
对于两条不重合的直线l1,l2,如果斜率存在,则有
注意:直线l1和l2可能重合,如果斜率存在,则有
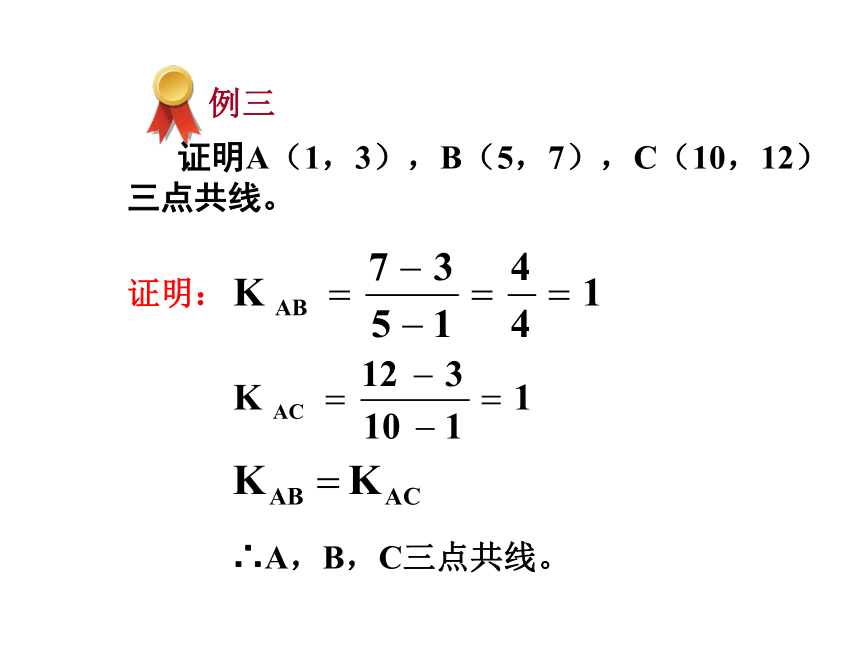
证明A(1,3),B(5,7),C(10,12)三点共线。
∴A,B,C三点共线。
证明:
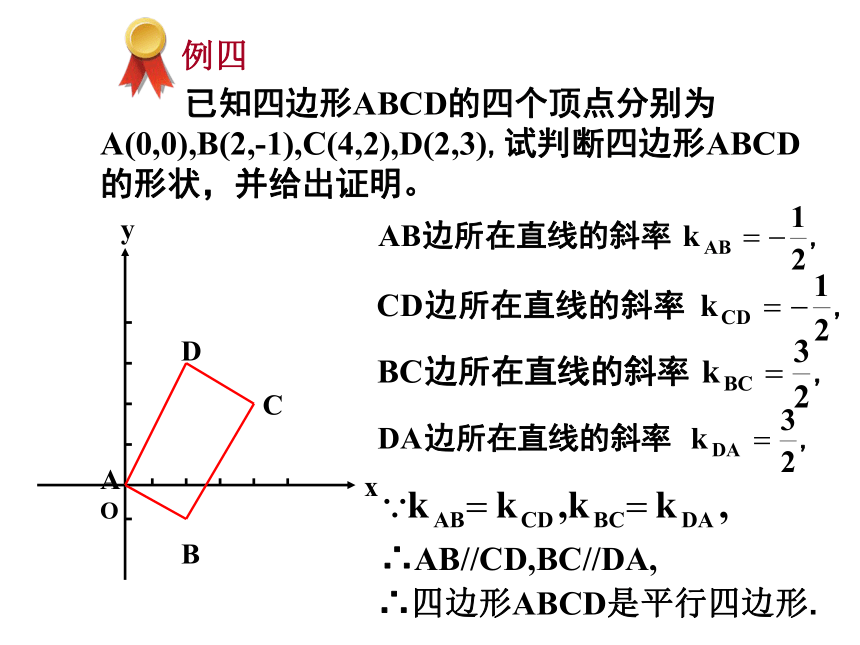
已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
A
B
C
D
∴AB//CD,BC//DA,
∴四边形ABCD是平行四边形.
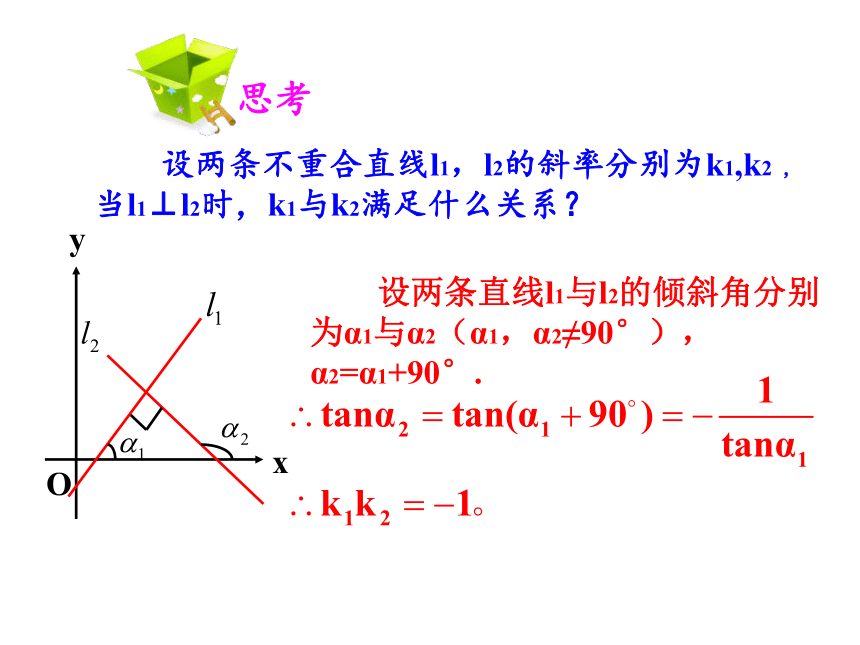
设两条不重合直线l1,l2的斜率分别为k1,k2 , 当l1⊥l2时,k1与k2满足什么关系?
设两条直线l1与l2的倾斜角分别为α1与α2(α1,α2≠90°),α2=α1+90°.
垂直
当k1k1 =-1时, l1与l2的位置关系如何?
由上我们得到,如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于-1;
反之,如果它们的斜率之积等于-1,那么它们互相垂直。
总结
L1// L2? k1=k2
L1⊥ L2? k1k2= -1
前提:两条直线不重合,且斜率都存在。
前提:两直线斜率都存在。
试确定m的值,使过点A(m,1),B(-1,m)的直线与过点P(1,2),Q(-5,0)的直线
(1)平行; (2)垂直。
设两条不重合直线l1,l2的斜率分别为k1,k2 , 当k1×k2=1时,l1与l2是什么样的位置关系?
两直线关于直线y=x对称。
两直线的倾斜角或都大于90°,或都小于90°。
设两条不重合直线l1,l2的斜率分别为k1,k2 , 当k1×k2>0时,l1与l2是什么样的位置关系?
两直线的倾斜角一个大于90°,一个小于90°。
设两条不重合直线l1,l2的斜率分别为k1,k2 , 当k1×k2<0时,l1与l2是什么样的位置关系?
已知A(5,-1),B(1,1),C(2,3)三点,试判断三角形ABC的形状。
一、知识内容上
L1// L2? k1=k2
L1⊥ L2? k1k2= -1
前提:两条直线不重合,且斜率都存在。
前提:两直线斜率都存在。
二、思想方法上
(1)运用代数方法研究几何性质及其相互位置关系。
(2)数形结合的思想。
1.已知a,b,c是两两不等的实数,求经过下列每两个点的直线的倾斜角。
(1)A(a,c),B(b,c)
(2)C(a,b),D(a,c)
(3)P(b,b+c),Q(a,c+a)
α=0°
α=90°
k=1 ,α=45°
解得 a=-3。
2.若A(3,2)、B(6,1),C(a,4)三点共线,则a的值等于多少?
解:
∵A,B,C三点共线
3.点M(1,2)在直线l上的射影是H(-1,4),求直线l的倾斜角。
∵直线AH与直线l垂直,
直线l的斜率为1,倾斜角为45°。
解:
4.已知A(1,-1),B(2,2),C(3,0)三点,求点D的坐标,使直线CD⊥AB,且CB//AD。
5. 已知A(-6,0),B(3,6),P(0,3),Q(6,-6),试判断直线AB与PQ的位置关系。
3.1.2 两条直线平行与垂直的判定
为了表示直线的倾斜程度,我们引入了直线倾斜角的概念。
进而引出斜率的概念,并导出了计算斜率的公式,即把几何问题转化为代数问题。
倾斜程度不同的直线斜率不同,那能不能通过直线的斜率来判断两直线的位置关系呢?
设两条不重合直线l1,l2的斜率分别为k1,k1 , 当l1//l2时,k1与k2满足什么关系?
若l1//l2,则 ,进而k1=k2,反之,若k1=k2,则l1//l2。
对于两条不重合的直线l1,l2,如果斜率存在,则有
注意:直线l1和l2可能重合,如果斜率存在,则有
证明A(1,3),B(5,7),C(10,12)三点共线。
∴A,B,C三点共线。
证明:
已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
A
B
C
D
∴AB//CD,BC//DA,
∴四边形ABCD是平行四边形.
设两条不重合直线l1,l2的斜率分别为k1,k2 , 当l1⊥l2时,k1与k2满足什么关系?
设两条直线l1与l2的倾斜角分别为α1与α2(α1,α2≠90°),α2=α1+90°.
垂直
当k1k1 =-1时, l1与l2的位置关系如何?
由上我们得到,如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于-1;
反之,如果它们的斜率之积等于-1,那么它们互相垂直。
总结
L1// L2? k1=k2
L1⊥ L2? k1k2= -1
前提:两条直线不重合,且斜率都存在。
前提:两直线斜率都存在。
试确定m的值,使过点A(m,1),B(-1,m)的直线与过点P(1,2),Q(-5,0)的直线
(1)平行; (2)垂直。
设两条不重合直线l1,l2的斜率分别为k1,k2 , 当k1×k2=1时,l1与l2是什么样的位置关系?
两直线关于直线y=x对称。
两直线的倾斜角或都大于90°,或都小于90°。
设两条不重合直线l1,l2的斜率分别为k1,k2 , 当k1×k2>0时,l1与l2是什么样的位置关系?
两直线的倾斜角一个大于90°,一个小于90°。
设两条不重合直线l1,l2的斜率分别为k1,k2 , 当k1×k2<0时,l1与l2是什么样的位置关系?
已知A(5,-1),B(1,1),C(2,3)三点,试判断三角形ABC的形状。
一、知识内容上
L1// L2? k1=k2
L1⊥ L2? k1k2= -1
前提:两条直线不重合,且斜率都存在。
前提:两直线斜率都存在。
二、思想方法上
(1)运用代数方法研究几何性质及其相互位置关系。
(2)数形结合的思想。
1.已知a,b,c是两两不等的实数,求经过下列每两个点的直线的倾斜角。
(1)A(a,c),B(b,c)
(2)C(a,b),D(a,c)
(3)P(b,b+c),Q(a,c+a)
α=0°
α=90°
k=1 ,α=45°
解得 a=-3。
2.若A(3,2)、B(6,1),C(a,4)三点共线,则a的值等于多少?
解:
∵A,B,C三点共线
3.点M(1,2)在直线l上的射影是H(-1,4),求直线l的倾斜角。
∵直线AH与直线l垂直,
直线l的斜率为1,倾斜角为45°。
解:
4.已知A(1,-1),B(2,2),C(3,0)三点,求点D的坐标,使直线CD⊥AB,且CB//AD。
5. 已知A(-6,0),B(3,6),P(0,3),Q(6,-6),试判断直线AB与PQ的位置关系。
