河南省2018-2019年度上学年高二年级期末考试数学(理科)(word版含答案)
文档属性
| 名称 | 河南省2018-2019年度上学年高二年级期末考试数学(理科)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 637.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 22:33:24 | ||
图片预览




文档简介
2018~2019年度上学年高二年级期末考试
数学(理科)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.设命题p:?x>0,|x|=x,则¬p为( )
A.?x>0,|x|≠x B.?x0≤0,|x0|=x0
C.?x≤0,|x|=x D.?x0>0,|x0|≠x0
2.已知抛物线的准线方程x,则抛物线的标准方程为( )
A.x2=2y B.x2=﹣2y C.y2=x D.y2=﹣2x
3.若等比数列{an}的前n项和为Sn,2a3+a6=0,则( )
A.﹣1 B.1 C.﹣2 D.2
4.函数f(x)=x3﹣ex的图象在x=1处的切线斜率为( )
A.3 B.3﹣e C.3+e D.e
5.在△ABC中,A,B,C所对的边分别为a,b,c,已知c=5,b=3,,则( )
A. B. C. D.
6.若函数f(x)=ax﹣lnx在[1,2]上单调递增,则a的取值范围是( )
A.(﹣∞,1] B.[1,+∞) C. D.(﹣∞,
7.若,则函数f(x)=ax+ex﹣1的图象在x=1处的切线方程为( )
A.2x﹣y=0 B.2x+y=0 C.x﹣2y=0 D.x+2y=0
8.“a,b,c,d成等差数列”是“a+d=b+c”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
9.函数f(x)的最小值为( )
A. B. C.2 D.
10.若x>1,则的最大值为( )
A. B. C. D.
11.已知函数f(x)的定义域为R,其导函数为f'(x),对任意x∈R,f'(x)>f(x)恒成立,且f(1)=1,则不等式ef(x)>ex的解集为( )
A.(1,+∞) B.[1,+∞) C.(﹣∞,0) D.(﹣∞,0]
12.设双曲线M:1(a>0,b>0)的上顶点为A,直线y与M交于B,C两点,过B,C分别作AC,AB的垂线交于点D若D到点(0,2)的距离不超过87a,则M的离心率的取值范围是( )
A.[1,+∞) B.[1,+∞) C.(1,1] D.(1,1]
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡中的横线上
13.若函数f(x)=x2,则f′(1)= .
14.若x,y满足约束条件,则z=2x﹣3y的最小值为 .
15.在正方体ABCD﹣A1B1C1D1中,M,N分别为AD,C1D1的中点,O为侧面BCC1B1的中心,则异面直线MN与OD1所成角的余弦值为 .
16.若函数y=sin2x+cos3x+a﹣1在区间[]上的最小值为0,则a= .
三、解答题:本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤
17.已知椭圆W:1(m>0,n>0)的离心率为e,长轴为AB,短轴为CD.
(1)若W的一个焦点为(3,0),|CD|=6,求W的方程;
(2)若|AB|=10,e,求W的方程.
18.在△ABC中,角A,B,C所对的边分别为a,b,c,已知2cos2A﹣cos2B=1,b+2acosC=0.
(1)求C;
(2)若,求△ABC的周长.
19.设函数f(x)=(x+1)2+axex.
(1)若a=1,求f(x)的极值;
(2)若a=﹣1,求f(x)的单调区间.
20.设等差数列{an}的前n项和为Sn,且S5=5S2,a6=6.
(1)求数列{an}的通项公式;
(2)求数列{an?3}的前n项和Tn.
21.已知函数f(x)=(a﹣b)x2﹣x﹣xlnx.
(1)若曲线y=f(x)在点(1,f(1)处的切线与x轴平行,且f(1)=a,求a,b的值;
(2)若a=1,f(x)≥0对x∈(0,+∞)恒成立,求b的取值范围.
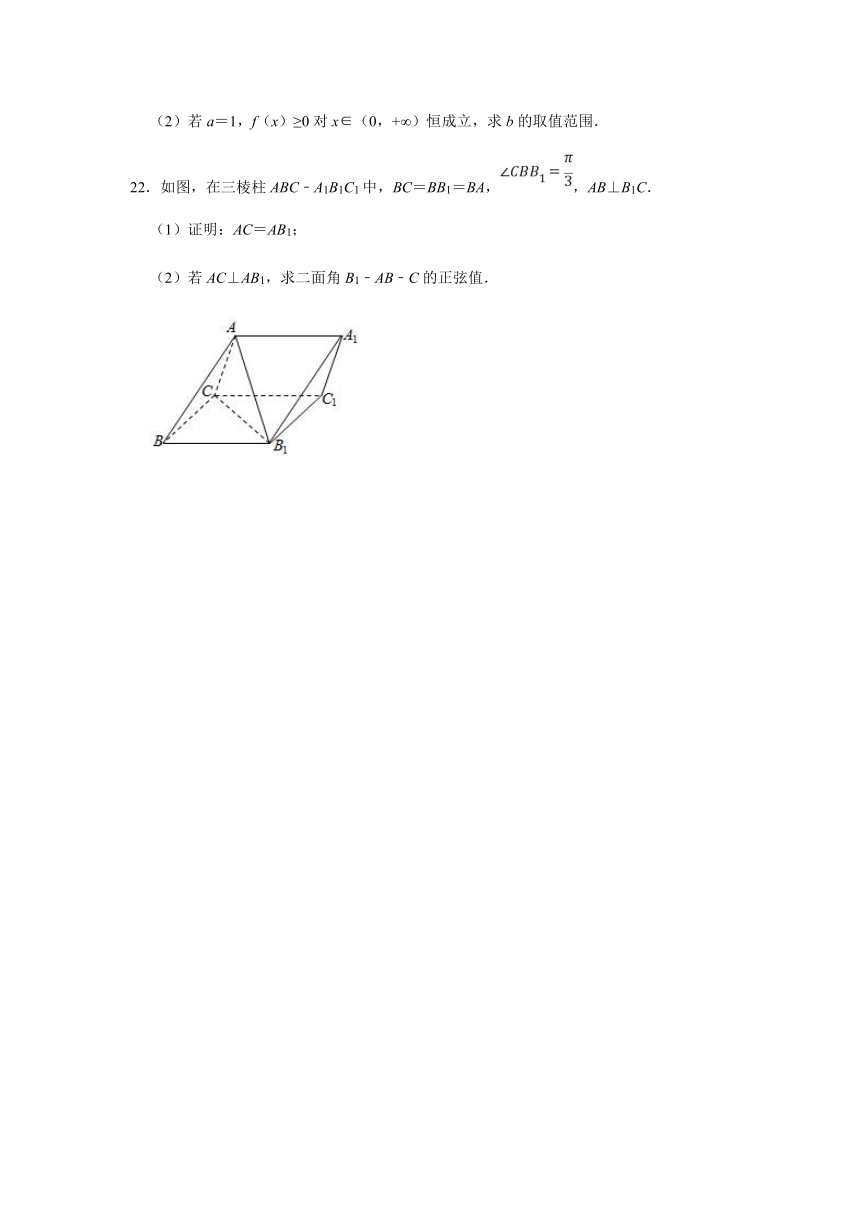
22.如图,在三棱柱ABC﹣A1B1C1中,BC=BB1=BA,,AB⊥B1C.
(1)证明:AC=AB1;
(2)若AC⊥AB1,求二面角B1﹣AB﹣C的正弦值.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.D
2.D
3.A
4.B
5.A
6.
7.A
8.A
9.D
10.C
11.A
12.D
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡中的横线上
13. 3.
14.﹣1
15..
16.函数y=sin2x+cos3x+a﹣1=﹣cos2x+cos3x+a,因为x∈[].所以cosx∈[0,1],
令t=cosx,则g(t)=t3﹣t2+a,g′(t)=3t2﹣2t=t(3t﹣2),t∈[0,1],
当t∈[0,]时,g′(t)≤0,当t∈(,1]时,g′(t)>0,
从而g(t)max=g()=a0,解得a.
三、解答题:本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤
17.(1)由已知可得,c=3,2b=6,b=3.
∴a2=b2+c2=18.
由题意可知,椭圆焦点在x轴上,则椭圆方程为;
(2)由已知可得,2a=10,则a=5,
又e,∴c=3,则b2=a2﹣c2=16.
若椭圆焦点在x轴上,则椭圆方程为.
若椭圆焦点在y轴上,则椭圆方程为.
18.(1)∵2cos2A﹣cos2B=1,
∴2(1﹣2sin2A)﹣(1﹣2sin2B)=1,
∴2sin2A=sin2B,
由正弦定理 可得,b2=2a2,
∵b+2acosC=0.
∴0,
∴cosC,
∵C∈(0,π),
∴C,
(2)∵,C,
由余弦定理可得,10,
5a2,
∴,b=2,
∴△ABC的周长2.
19.(1)a=1时,f(x)=(x+1)2+xex,
f′(x)=(x+1)(ex+2),
令f′(x)>0,解得:x>﹣1,
令f′(x)<0,解得:x<﹣1,
故f(x)在(﹣∞,﹣1)递减,在(﹣1,+∞)递增,
故f(x)极小值=f(﹣1),无极大值;
(2)证明:a=﹣1时,f(x)=(x+1)2﹣xex,
f′(x)=(x+1)(2﹣ex),
令f′(x)=0,解得:x=﹣1或x=ln2>0,
故x∈(﹣∞,﹣1),(ln2,+∞)时,f′(x)<0,
x∈(﹣1,ln2)时,f′(x)>0,
故f(x)在(﹣1,ln2)递增,在(﹣∞,﹣1),(ln2,+∞)递减.
20.(1)设等差数列{an}的公差为d,由,得a1=1,d=1,
故an=n;
(2)由,
,
两式作差,得:
﹣2,
故.
21.(1)函数f(x)=(a﹣b)x2﹣x﹣xlnx的导数为f′(x)=2(a﹣b)x﹣1﹣(1+lnx)=2(a﹣b)x﹣2﹣lnx,
在点(1,f(1)处的切线与x轴平行,且f(1)=a,可得
2(a﹣b)﹣2=0,且a﹣b﹣1=a,解得a=0,b=﹣1;
(2)a=1,f(x)≥0对x∈(0,+∞)恒成立,
即为(1﹣b)x2﹣x﹣xlnx≥0对x>0恒成立,
可得b≤(1)min,
设g(x)=1,
g′(x),
当0<x<1时,g′(x)<0,g(x)递减;x>1时,g′(x)>0,g(x)递增.
即有g(x)在x=1处取得最小值,且为0,
可得b≤0,
即b的取值范围是(﹣∞,0].
22.(1)证明:连接BC1,交B1C于点O,连接AO,
由题知,侧面BB1C1C为菱形,所以B1C⊥BC1,
又AB⊥B1C,AB∩BC1=B,所以B1C⊥平面ABO,
又AO?平面ABO,所以B1C⊥AO.
因为B1O=CO,所以AC=AB1.
(2)解:因为AC⊥AB1,所以AO=CO,又AB=BC,所以△BOA≌△BOC.
所以OA⊥OB,可知OA,OB,OB1两两垂直,以O为原点,建立如图空间直角坐标系O﹣xyz,
设,则A(0,0,1),,C(0,﹣1,0),B1(0,1,0),
所以,,,
设平面ABC的法向量为,
由,令y=3,得,
设平面B1AB的法向量为,
由,令x=1,得,
所以,
故二面角B1﹣AB﹣C的正弦值为.
