人教版数学九年级下册28.2.1解直角三角形-课件(1)(共20张PPT)
文档属性
| 名称 | 人教版数学九年级下册28.2.1解直角三角形-课件(1)(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 546.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
解直角三角形
知识回顾
问题探究
课堂小结
(2)勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方。
(1)锐角三角函数:在Rt△ABC中,∠A、∠B、∠C所对的边分别记为a、b、c,若∠C=90°,则 , ,
(4)含30°角的直角三角形的三边比为 ;含45°角的直角三角形的三边比为 。
(3)直角三角形两锐角互余。
知识回顾
问题探究
课堂小结
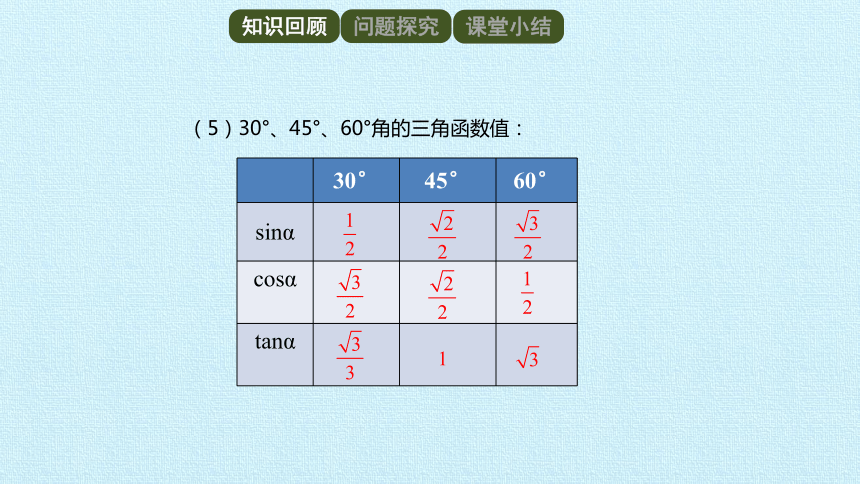
(5)30°、45°、60°角的三角函数值:
30° 45° 60°
sinα
cosα
tanα
知识回顾
问题探究
课堂小结
创设情境,引入新知
活动1
探究一:已知直角三角形中的两个元素能求出其他元素吗?
问题:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°<α<75°,如图现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1m)?
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人是否能够安全使用这个梯子?
分析:对于问题(1),当梯子与地面所成的角α 为75°时,梯子顶端与地面的距离是使用这个梯子所能攀到的最大高度。问题(1)可以归结为:在Rt△ABC中,已知∠A=75°,斜边AB=6,求∠A的对边BC的长。
分析:对于问题(2),当梯子底端距离墙面2.4m时,求梯子与地面所成的角α的问题,可以归结为:在Rt△ABC中,已知AC=2.4,斜边AB=6,求锐角α的度数。
知识回顾
问题探究
课堂小结
创设情境,引入新知
活动1
解:(1)由
得
由计算器求得 ,所以
因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m
探究一:已知直角三角形中的两个元素能求出其他元素吗?
问题:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°<α<75°,如图现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1m)?
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人是否能够安全使用这个梯子?
知识回顾
问题探究
课堂小结
创设情境,引入新知
活动1
探究一:已知直角三角形中的两个元素能求出其他元素吗?
问题:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°<α<75°,如图现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1m)?
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人是否能够安全使用这个梯子?
解:(2)由于 ,
利用计算器求得
因此当梯子底端距离墙面2.4m时,梯子与地面所成的角大约是66°
由 可知,这时使用这个梯子是安全的。
知识回顾
问题探究
课堂小结
探究一:已知直角三角形中的两个元素能求出其他元素吗?
探究思考,理论提升
活动2
思考:在上面问题的Rt△ABC中,
(2)根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?
(1)根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?
结论:可以,过程尝试自己写一下。
知识回顾
问题探究
课堂小结
解直角三角形
活动1
探究二:什么是解直角三角形?依据是什么?
1.一般地,我们把三角形的三个角∠A,∠B,∠C和它们的对边a,b,c叫做三角形的元素,即三角形共有六个元素。
2.在直角三角形中,由已知元素求未知元素的过程,就是解直角三角形。
3.在直角三角形中,除直角外共有5个元素,即3条边和2个锐角,如果已知两个元素(其中至少有一个是边),就可以求出其余的三个元素。即解直角三角形满足“知二推三”。
知识回顾
问题探究
课堂小结
探究二:什么是解直角三角形?依据是什么?
直角三角形各元素间的关系
活动1
直角三角形ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
(1)三边之间的关系:a2+b2=c2(勾股定理)
(2)两锐角之间的关系:∠A+∠B=90°
(3)边角之间的关系:
以上三点就是解直角三角形的依据。
知识回顾
问题探究
课堂小结
探究二:什么是解直角三角形?依据是什么?
应用新知,巩固练习
活动1
例1:如图,在Rt△ABC中,∠C=90°,BC= ,AC= ,解这个直角三角形。
解:
点拨:已知两边,用三角函数求出一角是突破口。
知识回顾
问题探究
课堂小结
探究二:什么是解直角三角形?依据是什么?
应用新知,巩固练习
活动1
例2:如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)。
解:
点拨:已知一边一角,用三角函数求出第二条边是突破口。
另外,解直角三角形的方法很多,在做题中要善于比较归纳、灵活处理。
知识回顾
问题探究
课堂小结
应用新知,回顾引言
活动2
探究三:怎样解直角三角形?
例3:如图,始建于1350年的意大利比萨斜塔落成时就已经倾斜。1972年比萨发生地震,这座高54.5m的斜塔大幅度摇摆22分之后,仍巍然屹立。可是,塔顶中心点偏离垂直中心线的距离已由落成时的2.1m增加至5.2m,而且还以每年倾斜1cm的速度继续增加,随时
都有倒塌的危险。为此,意大利当局从1990年起对斜塔
进行维修纠偏,2001年竣工,使塔顶中心点偏离垂直
中心线的距离比纠偏前减少了43.8cm,根据上面的信息,
你能用“塔身中心线偏离垂直中心线的角度”来描述
比萨斜塔的倾斜程度吗?
我们一起来解决关于比萨斜塔倾斜的问题。
知识回顾
问题探究
课堂小结
探究三:怎样解直角三角形?
应用新知,回顾引言
活动2
解:先看1972年的情形:设塔顶中心点为B,塔身中心线与垂直中心线的交点为A。
过B点向垂直中心线引垂线,垂足为C。
在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
sinA= ≈0.0954
所以∠A≈5°28′
类似地,可以求出2001年纠偏后塔身中心线与垂直中心线的夹角。
我们一起来解决关于比萨斜塔倾斜的问题。
知识回顾
问题探究
课堂小结
探究三:怎样解直角三角形?
常见类型,归纳提升
活动3
当图形中没有需要的直角三角形时,常常通过添加辅助线来构造直角三角形。
例1:如图,在△ABC中,已知BC= ,∠B=60°,∠C=45°,求AB的长。
D
解:如图,过点A作AD⊥BC,垂足为点D.
设BD=x,
在Rt△ABD中,AD=BD·tanB=x·tan60°= x
在Rt△ACD中,∵∠C=45°,∴∠CAD=90°-∠C=45°
∴∠C=∠CAD∴CD=AD= x
∵BC= ,∴ x+x= 解得x=1,即BD=1
在Rt△ABD中, ∵cos B= , ∴AB=
点拨:无直角的三角形常常作高,作高一般不破坏特殊角。
知识回顾
问题探究
课堂小结
探究三:怎样解直角三角形?
常见类型,归纳提升
活动3
例2:如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,∠D=∠B=90°,求四边形ABCD的面积。
解:如图,延长BC,AD交于点E
∵∠A=60°,∠B=90°,∴∠E=30°
在Rt△ABE中,BE= ,
在Rt△CDE中,EC=2CD=2. ∴DE=EC·cos 30°=
∴S四边形ABCD=SRt△ABE-SRt△ECD=
E
点拨:有直角、无三角形的图形常常延长某些边。本题看似是四边形问题,但注意到∠B=90°,∠A=60°,不难想到延长BC,AD,构造出直角三角形,将所求问题转化为直角三角形问题来解决。
知识回顾
问题探究
课堂小结
探究三:怎样解直角三角形?
常见类型,归纳提升
活动3
例3:如图,在△ABC中,点D为AB的中点,DC⊥AC,sin∠BCD= ,求tanA的值。
解:如图,过点B作BE⊥CD,交CD的延长线于点E。
E
∵点D是AB的中点,∴AD=DB
又∵∠ACD=∠BED=90°,∠ADC=∠BDE,
∴△ACD≌△BED,∴CD=DE,AC=BE
在Rt△CBE中,sin∠BCE= ,∴BC=3BE
∴CE , ∴
∴tan A=
点拨:有三角函数值不能直接利用时常常作垂线构造直角三角形,把所要求的量与已知量建立关系是解题的关键。
知识回顾
问题探究
课堂小结
探究三:怎样解直角三角形?
常见类型,归纳提升
活动3
例4:如图,在△ABC中,AB=AC=5,BC=8,若∠BPC= ∠BAC,求tan∠BPC的值。
解:如图,过点A作AE⊥BC于点E,
E
∵AB=AC=5,
∴BE ,∠BAE= ∠BAC
∵∠BPC= ∠BAC,∴∠BPC=∠BAE
在Rt△BAE中,由勾股定理得
AE= ,
∴tan∠BPC=tan∠BAE=
点拨:求角的三角函数值,若角不在直角三角形中、也不好构造直角三角形时,可以尝试将角转化到容易构造直角三角形的位置求解。
知识梳理
知识回顾
问题探究
课堂小结
(1)直角三角形各元素间的关系:
三边关系——勾股定理;
角的关系——两锐角互余;
边角关系——锐角三角函数。
(2)解直角三角形:在直角三角形中,由已知元素求未知元素的过程,就是解直角三角形。
(3)解直角三角形的一般方法
知识回顾
问题探究
课堂小结
重难点突破
(1)熟练掌握直角三角形边的关系、角的关系、边角关系是解直角三角形的关键。
(2)在做题过程中,抓住三角函数这一工具来求解,往往是简单可行的办法。
谢 谢
解直角三角形
知识回顾
问题探究
课堂小结
(2)勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方。
(1)锐角三角函数:在Rt△ABC中,∠A、∠B、∠C所对的边分别记为a、b、c,若∠C=90°,则 , ,
(4)含30°角的直角三角形的三边比为 ;含45°角的直角三角形的三边比为 。
(3)直角三角形两锐角互余。
知识回顾
问题探究
课堂小结
(5)30°、45°、60°角的三角函数值:
30° 45° 60°
sinα
cosα
tanα
知识回顾
问题探究
课堂小结
创设情境,引入新知
活动1
探究一:已知直角三角形中的两个元素能求出其他元素吗?
问题:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°<α<75°,如图现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1m)?
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人是否能够安全使用这个梯子?
分析:对于问题(1),当梯子与地面所成的角α 为75°时,梯子顶端与地面的距离是使用这个梯子所能攀到的最大高度。问题(1)可以归结为:在Rt△ABC中,已知∠A=75°,斜边AB=6,求∠A的对边BC的长。
分析:对于问题(2),当梯子底端距离墙面2.4m时,求梯子与地面所成的角α的问题,可以归结为:在Rt△ABC中,已知AC=2.4,斜边AB=6,求锐角α的度数。
知识回顾
问题探究
课堂小结
创设情境,引入新知
活动1
解:(1)由
得
由计算器求得 ,所以
因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m
探究一:已知直角三角形中的两个元素能求出其他元素吗?
问题:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°<α<75°,如图现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1m)?
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人是否能够安全使用这个梯子?
知识回顾
问题探究
课堂小结
创设情境,引入新知
活动1
探究一:已知直角三角形中的两个元素能求出其他元素吗?
问题:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°<α<75°,如图现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1m)?
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人是否能够安全使用这个梯子?
解:(2)由于 ,
利用计算器求得
因此当梯子底端距离墙面2.4m时,梯子与地面所成的角大约是66°
由 可知,这时使用这个梯子是安全的。
知识回顾
问题探究
课堂小结
探究一:已知直角三角形中的两个元素能求出其他元素吗?
探究思考,理论提升
活动2
思考:在上面问题的Rt△ABC中,
(2)根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?
(1)根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?
结论:可以,过程尝试自己写一下。
知识回顾
问题探究
课堂小结
解直角三角形
活动1
探究二:什么是解直角三角形?依据是什么?
1.一般地,我们把三角形的三个角∠A,∠B,∠C和它们的对边a,b,c叫做三角形的元素,即三角形共有六个元素。
2.在直角三角形中,由已知元素求未知元素的过程,就是解直角三角形。
3.在直角三角形中,除直角外共有5个元素,即3条边和2个锐角,如果已知两个元素(其中至少有一个是边),就可以求出其余的三个元素。即解直角三角形满足“知二推三”。
知识回顾
问题探究
课堂小结
探究二:什么是解直角三角形?依据是什么?
直角三角形各元素间的关系
活动1
直角三角形ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
(1)三边之间的关系:a2+b2=c2(勾股定理)
(2)两锐角之间的关系:∠A+∠B=90°
(3)边角之间的关系:
以上三点就是解直角三角形的依据。
知识回顾
问题探究
课堂小结
探究二:什么是解直角三角形?依据是什么?
应用新知,巩固练习
活动1
例1:如图,在Rt△ABC中,∠C=90°,BC= ,AC= ,解这个直角三角形。
解:
点拨:已知两边,用三角函数求出一角是突破口。
知识回顾
问题探究
课堂小结
探究二:什么是解直角三角形?依据是什么?
应用新知,巩固练习
活动1
例2:如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)。
解:
点拨:已知一边一角,用三角函数求出第二条边是突破口。
另外,解直角三角形的方法很多,在做题中要善于比较归纳、灵活处理。
知识回顾
问题探究
课堂小结
应用新知,回顾引言
活动2
探究三:怎样解直角三角形?
例3:如图,始建于1350年的意大利比萨斜塔落成时就已经倾斜。1972年比萨发生地震,这座高54.5m的斜塔大幅度摇摆22分之后,仍巍然屹立。可是,塔顶中心点偏离垂直中心线的距离已由落成时的2.1m增加至5.2m,而且还以每年倾斜1cm的速度继续增加,随时
都有倒塌的危险。为此,意大利当局从1990年起对斜塔
进行维修纠偏,2001年竣工,使塔顶中心点偏离垂直
中心线的距离比纠偏前减少了43.8cm,根据上面的信息,
你能用“塔身中心线偏离垂直中心线的角度”来描述
比萨斜塔的倾斜程度吗?
我们一起来解决关于比萨斜塔倾斜的问题。
知识回顾
问题探究
课堂小结
探究三:怎样解直角三角形?
应用新知,回顾引言
活动2
解:先看1972年的情形:设塔顶中心点为B,塔身中心线与垂直中心线的交点为A。
过B点向垂直中心线引垂线,垂足为C。
在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
sinA= ≈0.0954
所以∠A≈5°28′
类似地,可以求出2001年纠偏后塔身中心线与垂直中心线的夹角。
我们一起来解决关于比萨斜塔倾斜的问题。
知识回顾
问题探究
课堂小结
探究三:怎样解直角三角形?
常见类型,归纳提升
活动3
当图形中没有需要的直角三角形时,常常通过添加辅助线来构造直角三角形。
例1:如图,在△ABC中,已知BC= ,∠B=60°,∠C=45°,求AB的长。
D
解:如图,过点A作AD⊥BC,垂足为点D.
设BD=x,
在Rt△ABD中,AD=BD·tanB=x·tan60°= x
在Rt△ACD中,∵∠C=45°,∴∠CAD=90°-∠C=45°
∴∠C=∠CAD∴CD=AD= x
∵BC= ,∴ x+x= 解得x=1,即BD=1
在Rt△ABD中, ∵cos B= , ∴AB=
点拨:无直角的三角形常常作高,作高一般不破坏特殊角。
知识回顾
问题探究
课堂小结
探究三:怎样解直角三角形?
常见类型,归纳提升
活动3
例2:如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,∠D=∠B=90°,求四边形ABCD的面积。
解:如图,延长BC,AD交于点E
∵∠A=60°,∠B=90°,∴∠E=30°
在Rt△ABE中,BE= ,
在Rt△CDE中,EC=2CD=2. ∴DE=EC·cos 30°=
∴S四边形ABCD=SRt△ABE-SRt△ECD=
E
点拨:有直角、无三角形的图形常常延长某些边。本题看似是四边形问题,但注意到∠B=90°,∠A=60°,不难想到延长BC,AD,构造出直角三角形,将所求问题转化为直角三角形问题来解决。
知识回顾
问题探究
课堂小结
探究三:怎样解直角三角形?
常见类型,归纳提升
活动3
例3:如图,在△ABC中,点D为AB的中点,DC⊥AC,sin∠BCD= ,求tanA的值。
解:如图,过点B作BE⊥CD,交CD的延长线于点E。
E
∵点D是AB的中点,∴AD=DB
又∵∠ACD=∠BED=90°,∠ADC=∠BDE,
∴△ACD≌△BED,∴CD=DE,AC=BE
在Rt△CBE中,sin∠BCE= ,∴BC=3BE
∴CE , ∴
∴tan A=
点拨:有三角函数值不能直接利用时常常作垂线构造直角三角形,把所要求的量与已知量建立关系是解题的关键。
知识回顾
问题探究
课堂小结
探究三:怎样解直角三角形?
常见类型,归纳提升
活动3
例4:如图,在△ABC中,AB=AC=5,BC=8,若∠BPC= ∠BAC,求tan∠BPC的值。
解:如图,过点A作AE⊥BC于点E,
E
∵AB=AC=5,
∴BE ,∠BAE= ∠BAC
∵∠BPC= ∠BAC,∴∠BPC=∠BAE
在Rt△BAE中,由勾股定理得
AE= ,
∴tan∠BPC=tan∠BAE=
点拨:求角的三角函数值,若角不在直角三角形中、也不好构造直角三角形时,可以尝试将角转化到容易构造直角三角形的位置求解。
知识梳理
知识回顾
问题探究
课堂小结
(1)直角三角形各元素间的关系:
三边关系——勾股定理;
角的关系——两锐角互余;
边角关系——锐角三角函数。
(2)解直角三角形:在直角三角形中,由已知元素求未知元素的过程,就是解直角三角形。
(3)解直角三角形的一般方法
知识回顾
问题探究
课堂小结
重难点突破
(1)熟练掌握直角三角形边的关系、角的关系、边角关系是解直角三角形的关键。
(2)在做题过程中,抓住三角函数这一工具来求解,往往是简单可行的办法。
谢 谢
