2020年中考一轮复习--三角形综合(等腰三角形---直角三角形---勾股定理)教案设计(习题无答案)
文档属性
| 名称 | 2020年中考一轮复习--三角形综合(等腰三角形---直角三角形---勾股定理)教案设计(习题无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 210.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览

文档简介
三角形综合(等腰三角形 直角三角形 勾股定理)教案设计
学科: 任课教师: 学规师: 授课时间: 年 月 日 星期
姓名 年级 学校 总课时 第 课
教学 课题 三角形综合
教学 目标 知识点:等腰三角形 直角三角形 勾股定理考点:三线合一,斜边中线=斜边一半 旋转(辅助线) 任意三角形若知道三边长,求面积,(可以作一边的高,将原三角形分成两个直角三角形,另用勾股定理找等式求解)能力:综合能力 知识运用能力
难点 重点 难点:三线合一 旋转(辅助线) 重点:旋转(辅助线)
课前 检查 作业完成情况:优□ 良□ 中□ 差□ 建议__________________________________________
课堂教学过程
【第一部分 知识要点】
等腰三角形:
1.三线合一(重点);
2.有一个角为60度的等腰三角形是等边三角形。
直角三角形:
1.底角45度--等腰直角三角形
2.斜边中线=斜边一半;
3.旋转(辅助线)
4.30度,60度角所对边的应用;
勾股定理
1.直接用勾股定理求边
2.任意三角形若知道三边长,求面积,(可以作一边的高,将原三角形分成两个直角三角形,另用勾股定理找等式求解)
【第二部分:基础题训练】
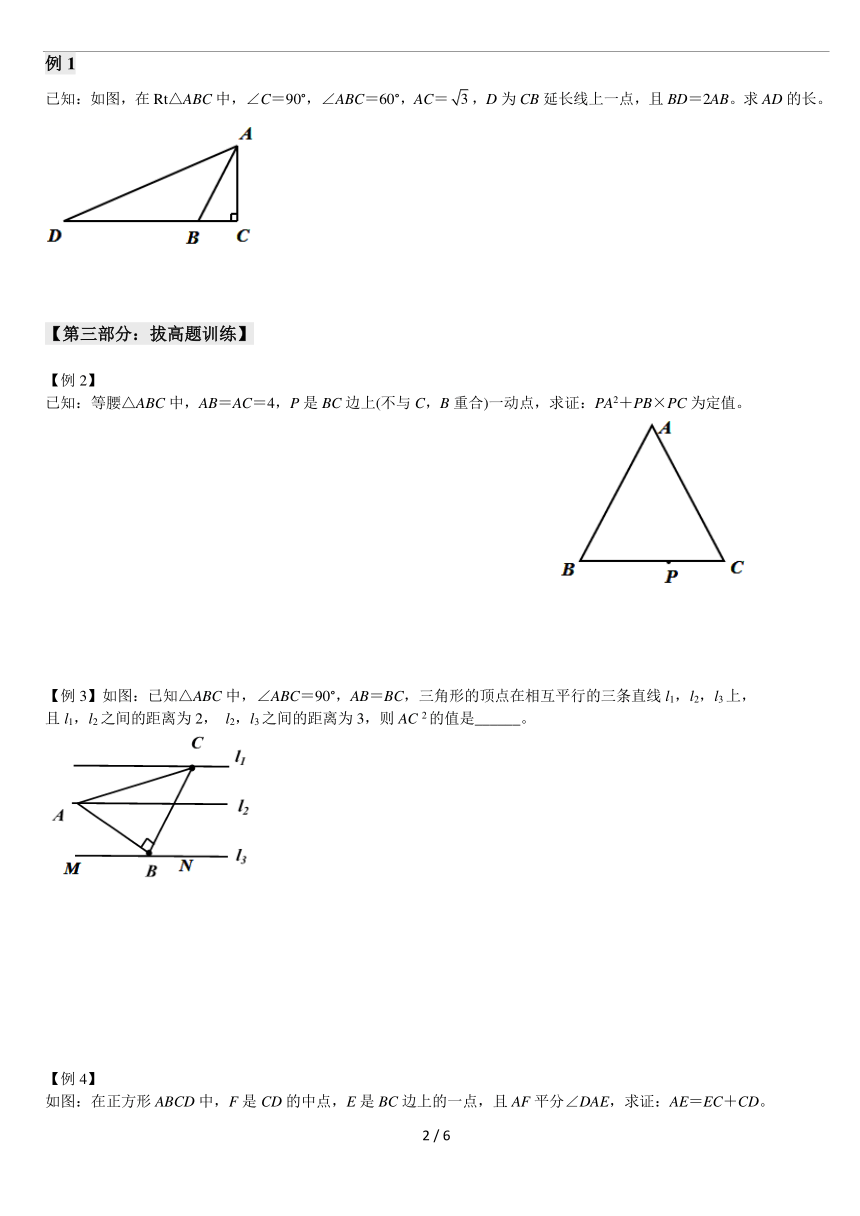
例1
已知:如图,在Rt△ABC中,∠C=90°,∠ABC=60°,AC=,D为CB延长线上一点,且BD=2AB。求AD的长。
【第三部分:拔高题训练】
【例2】
已知:等腰△ABC中,AB=AC=4,P是BC边上(不与C,B重合)一动点,求证:PA2+PB×PC为定值。
【例3】如图:已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2, l2,l3之间的距离为3,则AC 2的值是______。
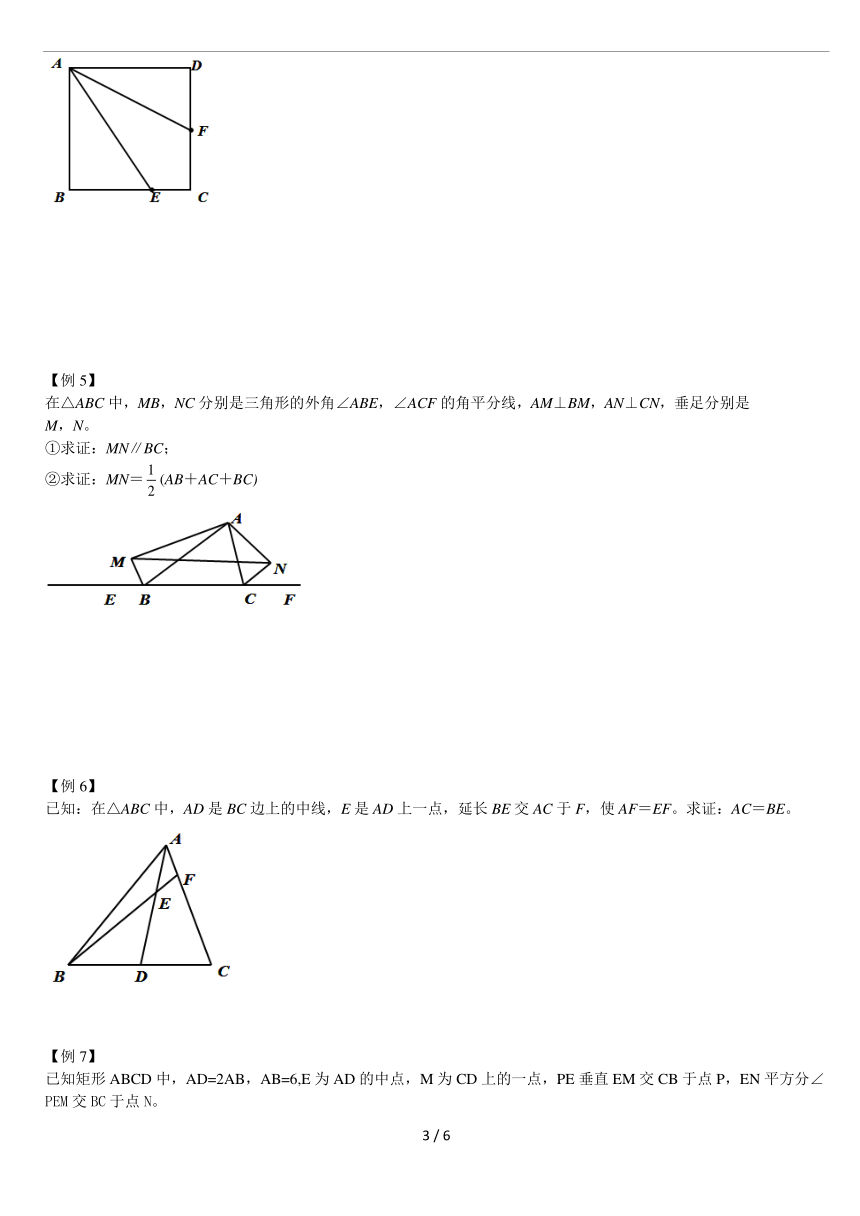
【例4】
如图:在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE,求证:AE=EC+CD。
【例5】
在△ABC中,MB,NC分别是三角形的外角∠ABE,∠ACF的角平分线,AM⊥BM,AN⊥CN,垂足分别是M,N。
①求证:MN∥BC;
②求证:MN=(AB+AC+BC)
【例6】
已知:在△ABC中,AD是BC边上的中线,E是AD上一点,延长BE交AC于F,使AF=EF。求证:AC=BE。
【例7】
已知矩形ABCD中,AD=2AB,AB=6,E为AD的中点,M为CD上的一点,PE垂直EM交CB于点P,EN平方分∠PEM交BC于点N。
:若△OEN为等腰三角形,请直接写出∠DEM所有可能的值。
判断BP? PN? NC?三者的数量关系,并加以证明
【例8】
如图 点E,F分别在正方形ABCD的BC,CD上,∠EAF=45?,试判断BE,EF,FD之间的数量关系。
【第四部分:本堂课小结】
附:
课后记 本节课教学计划完成情况:照常完成□ 提前完成□ 延后完成□
提交时间 学生的接收程度:完全能接受□ 部分能接受□ 不能接受□
学生的课堂表现:很积极□ 比较积极□ 一般□ 不积极□
学生上次作业完成情况:数量 ﹪ 完成质量 ﹪ 存在问题
备注
备注
【课后练习】
1.如图,四边形中,,,,,且,则四边形的面积是( )
A.96 B.150 C.246 D.262
2.如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN等于( )
A. B. C. D.
3.已知为的中线,,的平分线分别交于、交于。则的等量关系( )
A. B.
C. D.
4.如图所示,在四边形中,、分别为、的中点。
求证:。
5.如图,在中,交于点,点是中点,交的延长线于点,交于点,若,求证: 为的角平分线
6.已知:正方形中,,绕点顺时针旋转,它的两边分别交(或他们的延长线)于点,如图,当绕点旋转到时,的等量关系
E
E
D
A
N
P
M
C
B
D
A
F
C
B
E
PAGE / NUMPAGES
同课章节目录
