5.1.1 相交线(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 5.1.1 相交线(知识清单+经典例题+夯实基础+提优特训+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 389.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览




文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
人教版2019-2020学年度下学期七年级数学下册第五章相交线与平行线
5.1相交线
5.1.1相交线
【知识清单】
1.
两条直线相交:如果两条直线只有一个公共点,就说这两条直线相交.该公共点叫做这两条直线的交点.
如图(1)直线AB,CD相交于点O,形成4个角∠1,∠2,∠3,∠4.
2.邻补角:如∠1、∠2两个角有一条公共边,它们的另一条边互为反向延长线.
具有这种关系的两个角,互为邻补角.
3.对顶角:如∠1、∠3两个角有一个公共顶点,并且一个角的两条边,分别是另一个角的两条边的反向延长线,具有这种关系的两个角,互为对顶角.
4.对顶角的性质:对顶角相等.
【经典例题】
例题1、下列图中,既有对顶角,又有邻补角的是( )
【考点】对顶角、邻补角.
【分析】根据对顶角和邻补角定义进行逐个判定即可.
【解答】A、有邻补角没有对顶角,结论错误;
B、有邻补角没有对顶角,结论错误;;
C、有邻补角没有对顶角,结论错误;
D、符合定义,结论正确.
故选D.
【点评】本题考查的是对顶角与邻补角,熟知对顶角及邻补角的定义以及相关图形是解答此题的关键.
例题2、如图,已知直线a、b、c相交于点O,∠1:∠2:∠3=2:
3:4,则∠3=______.
【考点】对顶角、邻补角.
【分析】由图形可知,∠1+∠2+∠3是周角的一半,再把∠1,∠2代入便可求出∠3的度数.
【解答】由题意,得
∠1+∠2+∠3=×360°=180°.
设∠1=2x°,则∠1=3x°,∠3=4x°,
根据题意,得2x+3x+4x=180,
解得x=20°.
所以4x=80°.
故答案为:80°.
【点评】本题考查的是对顶角与平角,熟记对顶角及平角的定义以及方程的思想是解答此题的关键.
【夯实基础】
1.如图,∠1与∠2互为邻补角的是(
)
2.如图,直线AB,CD相交于点O.若∠1+∠2=80°,则∠3的度数为(
)
A.40°
B.100°
C.120°
D.140°
3.如图,直线EF与直线AB、CD分别相交于点E、F.若∠1+∠2=180°,则图中与∠1相等
的角(不含∠1)有(
)
A.4个
B.3个
C.2个
D.1个
4.∠1的对顶角是∠2,∠2的邻补角是∠3.若∠3=75°,则∠1的度数是(
)
A.15°
B.25°
C.15°或105°
D.105°
5.如图是一种对顶角量角器,它所测量到的角的度数是
,用它测量角的原理是
.
6.下列论断:①两个角有一条公共边,它们的另一条边互为反向延长线.
具有这种关系的两个
角,互为邻补角;②有公共顶点的两个角是对顶角;③对顶角相等;④如果两个角的和为180°,
那么这两个角为邻补角;⑤两个邻补角的平分线组成的角的度数一定为90°;⑥一个角的邻补角只有一个.其中正确的结论是
(填序号).
7.一个角的对顶角比它的邻补角的5倍还大12°,求这个角的度数.
8.如图,直线AB,CD相交于点O,OE平分∠DOB,OF平分∠COE,若∠AOC:∠COF=4:5,求∠DOF的度数.
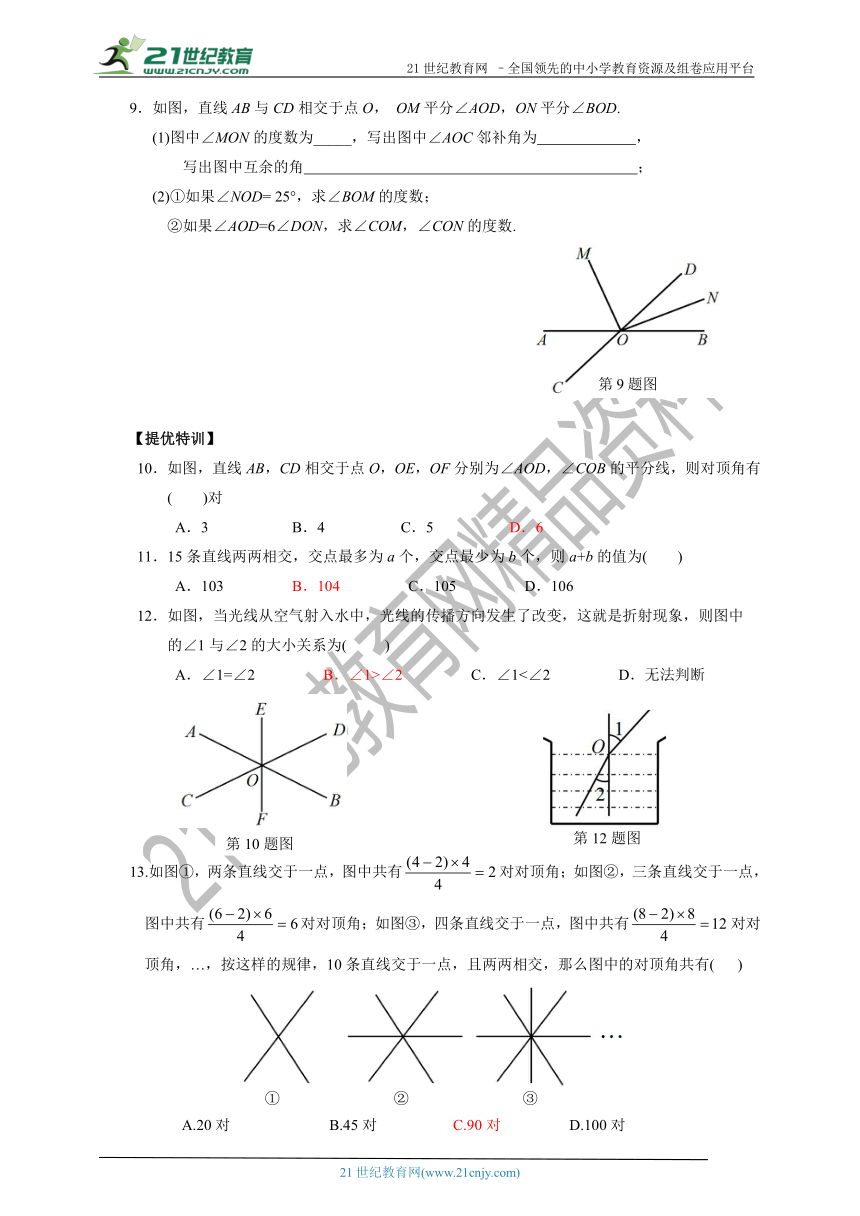
9.如图,直线AB与CD相交于点O,
OM平分∠AOD,ON平分∠BOD.
(1)图中∠MON的度数为_____,写出图中∠AOC邻补角为
,
写出图中互余的角
;
(2)①如果∠NOD=
25°,求∠BOM的度数;
②如果∠AOD=6∠DON,求∠COM,∠CON的度数.
【提优特训】
10.如图,直线AB,CD相交于点O,OE,OF分别为∠AOD,∠COB的平分线,则对顶角有( )对
A.3
B.4
C.5
D.6
11.15条直线两两相交,交点最多为a个,交点最少为b个,则a+b的值为(
)
A.103
B.104
C.105
D.106
12.如图,当光线从空气射入水中,光线的传播方向发生了改变,这就是折射现象,则图中
的∠1与∠2的大小关系为(
)
A.∠1=∠2
B.∠1>∠2
C.∠1<∠2
D.无法判断
13.如图①,两条直线交于一点,图中共有对对顶角;如图②,三条直线交于一点,
图中共有对对顶角;如图③,四条直线交于一点,图中共有对对
顶角,…,按这样的规律,10条直线交于一点,且两两相交,那么图中的对顶角共有(
)
A.20对
B.45对
C.90对
D.100对
14.已知∠AOB与∠BOC互为邻补角,且∠BOC>∠AOB,OD平分∠AOB,射线OE使
∠BOE=∠EOC.当∠DOE=
72°时,∠EOC的度数为
.
15.如图(1)是六棱柱实心体,有人想测量底部的∠ABC的度数,但人又不能进入六棱柱,只能站在六棱柱外,请问该如何测量
请你给出两个方案(1)
(2)
.
如图2()为了测量底部的角(图中∠ABC)的大小,某同学设计了两种测量方案:
方案1:作AB的延长线,量出∠CBF的度数,
便知∠ABC的度数;
方案2:作AB的延长线,CB的延长线,
量出∠EBF的度数,便知∠ABC的度数.
同学们,你能解释他这样做的道理吗?
16.动手操作,并回答问题(试画出示意图):
(1)如图①,1条直线可以把平面分成两个部分(或区域),2条直线最多可将平面分成几个部分3条直线最多可将平面分成几个部分?4条直线最多可以把平面分成几个部分?
(2)平面上有n条直线.两两相交,处于这种位置的n条直线分一个平面所成的区域最多,记为an,试研究an与n之间的关系.
17.
如图,直线AB,CD相交于点O,OC平分∠AOE,OF在∠EOB的内部,
∠EOF=∠FOB,∠COF=70°.求∠COE和∠FOD的度数.
18.如图,直线AB,CD相交于点O.已知∠AOD∶∠BOD=7∶5,OE把∠AOC分成两个角,
且∠EOC=∠AOE+15°.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.
19.如图,直线AB、CD、EF相交于点O.
(1)若∠1+∠2=62°,求∠3的度数;
(2)
若∠1:∠2:∠3=2:3:10,求∠COF的度数;
(3)
若∠3-∠2=96°,∠1=26°,求∠2的度数;
20.如图已知直线AB,CD相交于点O,∠1=40°,∠BOE与∠BOC互补,OM在∠BOE的
内部,且∠EOM∶∠MOB=2∶3,
∠COF∶∠FOM=3∶5.求∠COF和∠FOE的度数.
【中考链接】
21.(2019 模拟)
如图,直线a,b相交于点O,∠1+∠2=____°,∠2+∠3=
°(邻补角的定义),所以∠1________∠3(同角的补角相等).由此可知
对顶角_相等_________.
22.(2019 模拟)如图,直线AB,CD相交于点O,OE平分∠BOC,∠COF=90°.
(1)若∠BOE=72°,求∠AOF的度数;
(2)若∠BOD∶∠COE=1∶2,求∠AOF的度数.
参考答案
1、B
2、D
3、B
4、D
5、(1)30°,(2)对顶角相等
6、①③⑤
10、D
11、B
12、B
13、C
14、70°
21、180°
,180°
,=
,相等
7.一个角的对顶角比它的邻补角的5倍还大12°,求这个角的度数.
解:设这个角为x,则它的对顶角为x,邻补角为(180-x)
°,
根据题意得x5(180x)=12,
解得x=152°
8.解:设∠AOC=4x°,则∠COF=5x°,
∵直线AB,CD相交于点O,
∴∠AOC=∠BOD=4x°.
∵OE平分∠BOD,
∴∠BOE=∠DOE=∠BOD=2x°.
∵OF平分∠COE,
∴∠COF=∠EOF=5x°.
∴∠FOB=∠FOE∠BOE=5x°2x°=3x°.
∵∠AOC+∠COF+∠FOB=180°
∴
4x+5x+3x=180.
解得x=15°,
∴4x°=60°,
5x°=75°,
3x°=45°.
∴∠DOF=∠DOB+∠BOF=60°+45°=105°.
9.解:(2)
①∵ON平分∠BOD,
∴∠BON=∠DON.
∵∠NOD=
25°,
∴∠BON=∠DON=25°.
∴∠BOM=∠BON+∠NOM=25°+90°=115°.
②设∠DON=x°,则∠BON=x°,∠BOD=2x°,∠AOD=6x°,
∵∠AOD+∠DOB=180°,
∴6x+2x
=180.
解得x=22.5°.
∴6x=135°,
2x=45°.
∵∠AOM+∠BON=90°
∴∠AOM=90°∠BON=65°.
∵∠AOC=∠BOD=2x°=45°.
∴∠COM=∠AOC+∠AOM=65°+45°=110°.
∵∠AOC=45°,
∴∠BOC=180°∠AOC=180°-45°=135°.
∴∠CON=∠COB+∠BON=135+22.5°=157.5°.
或∠CON=180°∠DON=180°22.5°=157.5°.
15.
解:如图(2)方案1:利用了邻补角的性质;方案2:利用了对顶角相等的性质.
16.解:
(1)如图②,2条直线可以把平面至少分成3个部分,最多分成4个部分(直线是两两相交);
如图③,3条直线可以把平面至少分成4个部分,最多分成7个部分(直线是两两相交);
如图④,4条直线可以把平面至少分成5个部分,最多分成11个部分(直线是两两相交);
(2)根据以上的规律:1条直线可以把平面分成2=1+1部分,2条直线最多可以把平面
分成4=1+1+2部分,3条直线最多可以把平面分成7=1+1+2+3部分,4条直线最多
可以把平面分成11=1+1+2+3+4部分,则n条最多可以把平面分成1+1+2+3+…+n,
则an=.
17.
解:设∠3=x°,
∵∠COF=70°.
∴∠2=∠COF-∠3=(70-x)°.
∵∠EOF=∠FOB,
∴∠FOB=2∠EOF=2∠3=2x°.
∵OC平分∠AOE,
∴∠1=∠2=(70-x)°.
∵AB的直线,
∴∠AOB=180°.
∴∠1+∠2+∠3+∠FOB=180°.
70-x+70-x+x+2x=180
解得x=40°,2x=80°.
∴∠COE=∠2=(70-40)°=30°.
∴∠FOD=∠FOB+∠4=∠FOB+∠1=80°+30°=110°.
18.解:(1)∵∠AOD∶∠BOD=7∶5,
∴设∠AOD=7x,则∠DOB=5x,
∵∠AOD+∠BOD=180°,
∴7x+5x=180°,解得x=15°,则7x=105°,5x=75°.
∴∠AOD=7x
=105°,
∠DOB=5x=75°.
∵直线AB,CD相交于点O,
∴∠AOC=∠BOD=75°.
∴∠EOC+∠AOE=75°.
∴∠AOE+15°+∠AOE=75°.
解得∠AOE=30°.
(2)OB是∠DOF的平分线.理由如下:
∵∠AOE=30°,
∴∠BOE=180°∠AOE=150°,
∵OF平分∠BOE,
∴∠BOF=75°,
∵∠BOD=75°,
∴∠BOD=∠BOF,
∴OB是∠DOF的平分线.
19.解:(1)∵直线AB、CD、EF相交于点O.
∴∠1=∠DOF,∠2=∠AOE,
∵∠AOE+∠AOD+∠DOF=180°,
∴∠1+∠3+∠2=180°.
∠1+∠2=62°,
∠3=118°.
(2)设∠1=2x°,则∠2=3x°,∠3=10x°
∵∠2+∠3+∠1=180°,
∴2x+3x+10
x
=180.
解得x=12°,2x°=24°,3x°=36°,10
x°=120°.
∴∠COF
=180°∠1=180°24°=156°.
(3)设∠2=x°,则∠3=x°+96°,
∵∠AOE+∠3+∠DOF=180°,
∴∠2+∠3+∠1=180°,
即:x+
x+96+20=180.
解得x=32°,
∴∠2=32°.
20.
解:
∵直线AB,CD相交于点O,
∴∠AOC=∠1=40°.
∵∠BOE与∠BOC互补,∠AOC与∠BOC互为邻补,
∴
∠BOE=∠AOC=40°.
∵∠EOM∶∠MOB=2∶3,
设∠EOM=2x,则∠MOB=3x.
∵∠EOM+∠MOB=40°,
∴2x+3x=40°,
解得x=8°.
∴2x=16°,3x=24°.
∴∠EOM=2x=16°,
∠MOB=3x=24°.
∵∠COF∶∠FOM=3∶5,
设∠COF
=3x,则∠FOM
=5x.
∴∠COM=∠COF+∠FOM=∠AOB∠AOC∠BOM=180°40°24°=116°,
∴3x+5x=116
解得x=14.5°,
∴3x=43.5°,
5x=72.5°.
∴∠COF
=3x=43.5°,
∠FOM
=5x=72.5°.
∴∠FOE=∠FOM∠EOM=72.5°16°=56.5°.
【中考链接】
22.解:(1)∵OE平分∠BOC,
∴∠COE=∠BOE=∠BOC.
∵∠BOE=72°,
∴∠BOC=2∠BOE=144°.
∵∠AOC与∠COB为邻补角,
∴∠AOC+∠COB=180°.
∴∠AOC=180°∠COB=36°.
∵∠COF=90°,
∴∠AOF=90°∠AOC=54°.
(2)∵∠BOD∶∠COE=1∶2,
设∠BOD=x,则∠COE=2x,
∠BOE=2x.
∵∠COB与∠BOD为互为邻补角,
∴∠COB+∠BOD=180°,
∴2x+2x+x=180.
解得x=36°,
∵直线AB,CD相交于点O,
∴∠AOC=∠BOD=36°.
∵∠COF=90°,
∴∠AOF=90°∠AOC=54°.
A.
B.
C
D
第19题图
①
②
③
第8题图
第10题图
第15题图(1)
第20题图
第19题图
第22题图
第21题图
第9题图
第18题图
第17题图
第17题图
第12题图
例题2图
第15题图(2)
第2题图
图(1)
第18题图
第22题图
第3题图
第15题图(1)
第16题图①
第16题图②
第16题图③
第16题图④
A
B
C
D
第9题图
第5题图
第20题图
第8题图
第15题图(2)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
人教版2019-2020学年度下学期七年级数学下册第五章相交线与平行线
5.1相交线
5.1.1相交线
【知识清单】
1.
两条直线相交:如果两条直线只有一个公共点,就说这两条直线相交.该公共点叫做这两条直线的交点.
如图(1)直线AB,CD相交于点O,形成4个角∠1,∠2,∠3,∠4.
2.邻补角:如∠1、∠2两个角有一条公共边,它们的另一条边互为反向延长线.
具有这种关系的两个角,互为邻补角.
3.对顶角:如∠1、∠3两个角有一个公共顶点,并且一个角的两条边,分别是另一个角的两条边的反向延长线,具有这种关系的两个角,互为对顶角.
4.对顶角的性质:对顶角相等.
【经典例题】
例题1、下列图中,既有对顶角,又有邻补角的是( )
【考点】对顶角、邻补角.
【分析】根据对顶角和邻补角定义进行逐个判定即可.
【解答】A、有邻补角没有对顶角,结论错误;
B、有邻补角没有对顶角,结论错误;;
C、有邻补角没有对顶角,结论错误;
D、符合定义,结论正确.
故选D.
【点评】本题考查的是对顶角与邻补角,熟知对顶角及邻补角的定义以及相关图形是解答此题的关键.
例题2、如图,已知直线a、b、c相交于点O,∠1:∠2:∠3=2:
3:4,则∠3=______.
【考点】对顶角、邻补角.
【分析】由图形可知,∠1+∠2+∠3是周角的一半,再把∠1,∠2代入便可求出∠3的度数.
【解答】由题意,得
∠1+∠2+∠3=×360°=180°.
设∠1=2x°,则∠1=3x°,∠3=4x°,
根据题意,得2x+3x+4x=180,
解得x=20°.
所以4x=80°.
故答案为:80°.
【点评】本题考查的是对顶角与平角,熟记对顶角及平角的定义以及方程的思想是解答此题的关键.
【夯实基础】
1.如图,∠1与∠2互为邻补角的是(
)
2.如图,直线AB,CD相交于点O.若∠1+∠2=80°,则∠3的度数为(
)
A.40°
B.100°
C.120°
D.140°
3.如图,直线EF与直线AB、CD分别相交于点E、F.若∠1+∠2=180°,则图中与∠1相等
的角(不含∠1)有(
)
A.4个
B.3个
C.2个
D.1个
4.∠1的对顶角是∠2,∠2的邻补角是∠3.若∠3=75°,则∠1的度数是(
)
A.15°
B.25°
C.15°或105°
D.105°
5.如图是一种对顶角量角器,它所测量到的角的度数是
,用它测量角的原理是
.
6.下列论断:①两个角有一条公共边,它们的另一条边互为反向延长线.
具有这种关系的两个
角,互为邻补角;②有公共顶点的两个角是对顶角;③对顶角相等;④如果两个角的和为180°,
那么这两个角为邻补角;⑤两个邻补角的平分线组成的角的度数一定为90°;⑥一个角的邻补角只有一个.其中正确的结论是
(填序号).
7.一个角的对顶角比它的邻补角的5倍还大12°,求这个角的度数.
8.如图,直线AB,CD相交于点O,OE平分∠DOB,OF平分∠COE,若∠AOC:∠COF=4:5,求∠DOF的度数.
9.如图,直线AB与CD相交于点O,
OM平分∠AOD,ON平分∠BOD.
(1)图中∠MON的度数为_____,写出图中∠AOC邻补角为
,
写出图中互余的角
;
(2)①如果∠NOD=
25°,求∠BOM的度数;
②如果∠AOD=6∠DON,求∠COM,∠CON的度数.
【提优特训】
10.如图,直线AB,CD相交于点O,OE,OF分别为∠AOD,∠COB的平分线,则对顶角有( )对
A.3
B.4
C.5
D.6
11.15条直线两两相交,交点最多为a个,交点最少为b个,则a+b的值为(
)
A.103
B.104
C.105
D.106
12.如图,当光线从空气射入水中,光线的传播方向发生了改变,这就是折射现象,则图中
的∠1与∠2的大小关系为(
)
A.∠1=∠2
B.∠1>∠2
C.∠1<∠2
D.无法判断
13.如图①,两条直线交于一点,图中共有对对顶角;如图②,三条直线交于一点,
图中共有对对顶角;如图③,四条直线交于一点,图中共有对对
顶角,…,按这样的规律,10条直线交于一点,且两两相交,那么图中的对顶角共有(
)
A.20对
B.45对
C.90对
D.100对
14.已知∠AOB与∠BOC互为邻补角,且∠BOC>∠AOB,OD平分∠AOB,射线OE使
∠BOE=∠EOC.当∠DOE=
72°时,∠EOC的度数为
.
15.如图(1)是六棱柱实心体,有人想测量底部的∠ABC的度数,但人又不能进入六棱柱,只能站在六棱柱外,请问该如何测量
请你给出两个方案(1)
(2)
.
如图2()为了测量底部的角(图中∠ABC)的大小,某同学设计了两种测量方案:
方案1:作AB的延长线,量出∠CBF的度数,
便知∠ABC的度数;
方案2:作AB的延长线,CB的延长线,
量出∠EBF的度数,便知∠ABC的度数.
同学们,你能解释他这样做的道理吗?
16.动手操作,并回答问题(试画出示意图):
(1)如图①,1条直线可以把平面分成两个部分(或区域),2条直线最多可将平面分成几个部分3条直线最多可将平面分成几个部分?4条直线最多可以把平面分成几个部分?
(2)平面上有n条直线.两两相交,处于这种位置的n条直线分一个平面所成的区域最多,记为an,试研究an与n之间的关系.
17.
如图,直线AB,CD相交于点O,OC平分∠AOE,OF在∠EOB的内部,
∠EOF=∠FOB,∠COF=70°.求∠COE和∠FOD的度数.
18.如图,直线AB,CD相交于点O.已知∠AOD∶∠BOD=7∶5,OE把∠AOC分成两个角,
且∠EOC=∠AOE+15°.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.
19.如图,直线AB、CD、EF相交于点O.
(1)若∠1+∠2=62°,求∠3的度数;
(2)
若∠1:∠2:∠3=2:3:10,求∠COF的度数;
(3)
若∠3-∠2=96°,∠1=26°,求∠2的度数;
20.如图已知直线AB,CD相交于点O,∠1=40°,∠BOE与∠BOC互补,OM在∠BOE的
内部,且∠EOM∶∠MOB=2∶3,
∠COF∶∠FOM=3∶5.求∠COF和∠FOE的度数.
【中考链接】
21.(2019 模拟)
如图,直线a,b相交于点O,∠1+∠2=____°,∠2+∠3=
°(邻补角的定义),所以∠1________∠3(同角的补角相等).由此可知
对顶角_相等_________.
22.(2019 模拟)如图,直线AB,CD相交于点O,OE平分∠BOC,∠COF=90°.
(1)若∠BOE=72°,求∠AOF的度数;
(2)若∠BOD∶∠COE=1∶2,求∠AOF的度数.
参考答案
1、B
2、D
3、B
4、D
5、(1)30°,(2)对顶角相等
6、①③⑤
10、D
11、B
12、B
13、C
14、70°
21、180°
,180°
,=
,相等
7.一个角的对顶角比它的邻补角的5倍还大12°,求这个角的度数.
解:设这个角为x,则它的对顶角为x,邻补角为(180-x)
°,
根据题意得x5(180x)=12,
解得x=152°
8.解:设∠AOC=4x°,则∠COF=5x°,
∵直线AB,CD相交于点O,
∴∠AOC=∠BOD=4x°.
∵OE平分∠BOD,
∴∠BOE=∠DOE=∠BOD=2x°.
∵OF平分∠COE,
∴∠COF=∠EOF=5x°.
∴∠FOB=∠FOE∠BOE=5x°2x°=3x°.
∵∠AOC+∠COF+∠FOB=180°
∴
4x+5x+3x=180.
解得x=15°,
∴4x°=60°,
5x°=75°,
3x°=45°.
∴∠DOF=∠DOB+∠BOF=60°+45°=105°.
9.解:(2)
①∵ON平分∠BOD,
∴∠BON=∠DON.
∵∠NOD=
25°,
∴∠BON=∠DON=25°.
∴∠BOM=∠BON+∠NOM=25°+90°=115°.
②设∠DON=x°,则∠BON=x°,∠BOD=2x°,∠AOD=6x°,
∵∠AOD+∠DOB=180°,
∴6x+2x
=180.
解得x=22.5°.
∴6x=135°,
2x=45°.
∵∠AOM+∠BON=90°
∴∠AOM=90°∠BON=65°.
∵∠AOC=∠BOD=2x°=45°.
∴∠COM=∠AOC+∠AOM=65°+45°=110°.
∵∠AOC=45°,
∴∠BOC=180°∠AOC=180°-45°=135°.
∴∠CON=∠COB+∠BON=135+22.5°=157.5°.
或∠CON=180°∠DON=180°22.5°=157.5°.
15.
解:如图(2)方案1:利用了邻补角的性质;方案2:利用了对顶角相等的性质.
16.解:
(1)如图②,2条直线可以把平面至少分成3个部分,最多分成4个部分(直线是两两相交);
如图③,3条直线可以把平面至少分成4个部分,最多分成7个部分(直线是两两相交);
如图④,4条直线可以把平面至少分成5个部分,最多分成11个部分(直线是两两相交);
(2)根据以上的规律:1条直线可以把平面分成2=1+1部分,2条直线最多可以把平面
分成4=1+1+2部分,3条直线最多可以把平面分成7=1+1+2+3部分,4条直线最多
可以把平面分成11=1+1+2+3+4部分,则n条最多可以把平面分成1+1+2+3+…+n,
则an=.
17.
解:设∠3=x°,
∵∠COF=70°.
∴∠2=∠COF-∠3=(70-x)°.
∵∠EOF=∠FOB,
∴∠FOB=2∠EOF=2∠3=2x°.
∵OC平分∠AOE,
∴∠1=∠2=(70-x)°.
∵AB的直线,
∴∠AOB=180°.
∴∠1+∠2+∠3+∠FOB=180°.
70-x+70-x+x+2x=180
解得x=40°,2x=80°.
∴∠COE=∠2=(70-40)°=30°.
∴∠FOD=∠FOB+∠4=∠FOB+∠1=80°+30°=110°.
18.解:(1)∵∠AOD∶∠BOD=7∶5,
∴设∠AOD=7x,则∠DOB=5x,
∵∠AOD+∠BOD=180°,
∴7x+5x=180°,解得x=15°,则7x=105°,5x=75°.
∴∠AOD=7x
=105°,
∠DOB=5x=75°.
∵直线AB,CD相交于点O,
∴∠AOC=∠BOD=75°.
∴∠EOC+∠AOE=75°.
∴∠AOE+15°+∠AOE=75°.
解得∠AOE=30°.
(2)OB是∠DOF的平分线.理由如下:
∵∠AOE=30°,
∴∠BOE=180°∠AOE=150°,
∵OF平分∠BOE,
∴∠BOF=75°,
∵∠BOD=75°,
∴∠BOD=∠BOF,
∴OB是∠DOF的平分线.
19.解:(1)∵直线AB、CD、EF相交于点O.
∴∠1=∠DOF,∠2=∠AOE,
∵∠AOE+∠AOD+∠DOF=180°,
∴∠1+∠3+∠2=180°.
∠1+∠2=62°,
∠3=118°.
(2)设∠1=2x°,则∠2=3x°,∠3=10x°
∵∠2+∠3+∠1=180°,
∴2x+3x+10
x
=180.
解得x=12°,2x°=24°,3x°=36°,10
x°=120°.
∴∠COF
=180°∠1=180°24°=156°.
(3)设∠2=x°,则∠3=x°+96°,
∵∠AOE+∠3+∠DOF=180°,
∴∠2+∠3+∠1=180°,
即:x+
x+96+20=180.
解得x=32°,
∴∠2=32°.
20.
解:
∵直线AB,CD相交于点O,
∴∠AOC=∠1=40°.
∵∠BOE与∠BOC互补,∠AOC与∠BOC互为邻补,
∴
∠BOE=∠AOC=40°.
∵∠EOM∶∠MOB=2∶3,
设∠EOM=2x,则∠MOB=3x.
∵∠EOM+∠MOB=40°,
∴2x+3x=40°,
解得x=8°.
∴2x=16°,3x=24°.
∴∠EOM=2x=16°,
∠MOB=3x=24°.
∵∠COF∶∠FOM=3∶5,
设∠COF
=3x,则∠FOM
=5x.
∴∠COM=∠COF+∠FOM=∠AOB∠AOC∠BOM=180°40°24°=116°,
∴3x+5x=116
解得x=14.5°,
∴3x=43.5°,
5x=72.5°.
∴∠COF
=3x=43.5°,
∠FOM
=5x=72.5°.
∴∠FOE=∠FOM∠EOM=72.5°16°=56.5°.
【中考链接】
22.解:(1)∵OE平分∠BOC,
∴∠COE=∠BOE=∠BOC.
∵∠BOE=72°,
∴∠BOC=2∠BOE=144°.
∵∠AOC与∠COB为邻补角,
∴∠AOC+∠COB=180°.
∴∠AOC=180°∠COB=36°.
∵∠COF=90°,
∴∠AOF=90°∠AOC=54°.
(2)∵∠BOD∶∠COE=1∶2,
设∠BOD=x,则∠COE=2x,
∠BOE=2x.
∵∠COB与∠BOD为互为邻补角,
∴∠COB+∠BOD=180°,
∴2x+2x+x=180.
解得x=36°,
∵直线AB,CD相交于点O,
∴∠AOC=∠BOD=36°.
∵∠COF=90°,
∴∠AOF=90°∠AOC=54°.
A.
B.
C
D
第19题图
①
②
③
第8题图
第10题图
第15题图(1)
第20题图
第19题图
第22题图
第21题图
第9题图
第18题图
第17题图
第17题图
第12题图
例题2图
第15题图(2)
第2题图
图(1)
第18题图
第22题图
第3题图
第15题图(1)
第16题图①
第16题图②
第16题图③
第16题图④
A
B
C
D
第9题图
第5题图
第20题图
第8题图
第15题图(2)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
