高中数学人教A版(2019)必修第一册第四章教案4.2指数函数(pdf版)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册第四章教案4.2指数函数(pdf版) |

|
|
| 格式 | zip | ||
| 文件大小 | 735.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 00:00:00 | ||
图片预览


文档简介
4.2 指数函数 (2课时,单元教学设计 )
-、 内容和内容解析
1.内容
本单元的知识结构如下 :
∷指数函数 :
「
ˉ? ~^ˉ ˉ?~~T— —— —~¨ ~ˉ
l
「蔽Π 「蔟l i∴哳1
本单元包括指数函数的概念、图象和性质,它们是中学数学中的重要内容。本单元共 2课
时,第 1课时的主要内容是指数函数的概念,第 2课时的主要内容是指数函数的图象和性质。
2。 内容解析
本单元是在函数的概念和性质、幂函数、指数及其运算性质的基础上,进一步研究指数函数
的概念、图象和性质。指数函数作为基本初等函数之一,是函数内容的重要组成部分;是对数函
数、等比数列、概率统计、导数等高中数学内容的基础,其思想方法与其他数学内容还有紧密的
联系;同时作为重要的函数模型还有广泛的应用,又是分析和解决大量数学问题和实际问题的重
要工具.
指数函数是一类具体的函数,有了研究幂函数的经验,便可以按研究一个函数的基本方法去
研究指数函数的主要内容.指数函数的概念体现了指数函数变量间对应关系的本质,图象和性质
则是在概念基础上进一步研究其变化规律,应该从概念出发认识图象和性质,并结合图象和性质
进一步理解概念。
指数函数是刻画呈指数增长或衰减变化规律的函数模型,其概念的教学,应该在函数概念的
基础上,重点揭示指数增长或衰减的规律:在 自变量增加 1个单位,即 自变量从£0变化到幻+1
时,相应的函数值之比
甜
=Ω 为音数,这反映了指数函数变化规律的特征。教学时要引导
学生通过实例抽象概括出这个特点,以使学生明确指数函数所刻画的现实问题的类型。
指数函数是指形如γ=α
£铴)0,且 α≠1)的函数,当 曰>1时 ,函数以指数增长;当 0(曰 (1
时,函数以指数衰减。对于指数函数图象和性质的研究,应从函数 y=Ω=(c>0,且 c≠ D出发 ,
通过Ω取不同值时函数的图象直观地体现指数函数的变化规律;然后在大量具体图象的基础上归纳
其共同特征,并选择有代表性的图象反映这样的特征,说明函数的定义域、值域、特殊点、单调
性。由函数的图象能体现函数的性质,而由函数的性质也能确定函数的图象特征,教学应突出这种
数形结合的思想方法,并通过解析式、图象、性质多元联系地认识指数函数的本质和函数模型的
特征。
|第四章 指数函数与对数函数 |203
根据上述分析,确定本单元的教学重点:指数函数的概念、图象和性质.
二、目标和目标解析
1.目标
(1)通过具体实例,了解指数函数的实际意义,理解指数函数的概念。
(2)能用描点法或借助信息技术画出具体指数函数的图象,探索并理解指数函数的单调性与
特殊点。
(3)结合指数函数概念、图象与性质的研究,进一步体会研究具体函数的一般思路和方法 ,
提升数学抽象、直观想象素养.
2.目标解析
达成上述目标的标志是 :
(1)能结合教科书中游客增长的问题 1和碳 14衰减的问题 2,通过运算发现其中具体的增长
或衰减的规律,并从中体会实际问题中变量间的关系。在了解指数函数的实际意义的基础上,知
道指数函数的含义和表示,清楚其定义域和底数Ω的取值范围。
(2)能根据函数解析式或利用计算工具计算出指数函数的两个变量的一些对应值并列表,然
后描点或利用信息技术画出指数函数的图象,或能根据函数解析式直接利用信息技术画出指数函
数的图象;结合函数图象,归纳这些图象的共同特征,探索并总结指数函数的单调性与特殊点 ,
并结合函数解析式验证所
`总
结的函数单调性和特殊点。
(3)结合指数函数的教学,体会 “概念一图象一性质”的研究具体函数的一般思路;在由具
体实例抽象为具体函数、再由具体函数概括为指数函数的过程,提升数学抽象素养;结合由函数
图象直观认识函数性质的过程,体会数形结合的思想方法,提升直观想象素养。
三、教学问题诊断分析
本单元中由具体实例抽象出指数函数的概念,不仅要能想到将问题 1游客人次的变化用图象
直观表示,还要能结合图象对已知数据进行运算后发现变化规律,并能根据问题 1和问题 2得到
的两个解析式概括出统一的函数关系式丿=aJ(厶)0,且 c≠ D。 这些对学生思维能力的要求较
高。教学中,教师要给学生探索和发现的机会,并给予学生恰当的指导.在学生不能从问题 1的
数据中发现游客人次的变化规律时,可引导学生先根据已知数据作出图象进行观察,然后启发学
生对已知数据进行运算,通过运算得到每年与上一年旅游人次的比例为常数,从而结合图象发现
变化规律的本质。这里,对数据进行哪些运算才有利于发现规律,是学生已有知识经验中缺乏
的,教学中需要引导学生注意,并注意边空中对
“
增加量
”“
增长率
”
的作用的强调.
要从不同具体问题得到的解析式概括出γ=Ω
£
的形式,可能需要指导学生将问题 2的解析式
整理为 y=((:)573°
)=·
教学中还要引导学生利用信息技术,从指数幂的意义、函数的对应关系
和图象出发,结合实例理解指数函数底数的取值范围,并在学习对数和对数函数后进一步理解。
在指数函数性质的学习过程中,尽管学生已经历过幂函数性质的学习,但那是在给定的五个
具体函数基础上进行不完整、不系统的归纳,而且幂函数性质不
“
规整
”,典型性有所欠缺,难
以完全指导其他基本初等函数的研究.指数函数性质的探索则需要学生自行选择具体的函数,必
要时教师可引导学生利用信息技术进行探索,通过画出底数 a取大量不同值时的图象,发现并归
纳函数的单调性;在探索的基础上将大量所作的图象分为增长和衰减两类,利用信息技术分别研
200|普通高中教科书教师教学用书 数学 必修 第一册 |
究两类图象函数值的变化,从而归纳出G)1时函数单调递增,0(曰 (1时函数单调递减.
本单元的教学难点是用
“
增长率
”
刻画变化规律,以及指数函数单调性的抽象概括。
四、教学支持条件分析
在本单元的教学中,可以利用信息技术中的 Exce1、 函数作图等软件工具进行计算、列表和
作图,以便于多元联系地表示指数函数,帮助学生克服学习中可能遇到的困难,更好地理解指数
函数的概念和性质。在指数函数概念的教学中,利用信息技术可以很方便地将问题 1中表格的数
据转化为图象,由 图象直观地发现旅游人次的整体变化情况;然后利用信息技术对这些数据进行
计算,通过计算揭示图象蕴含的变化规律的本质。在指数函数图象和性质的教学中,利用信息技
术可以进行多种方式的研究,比如任意作出大量需要的函数图象,通过观察图象归纳出不同图象
的共同特征,进而抽象出函数的性质;又如建立函数的图象和数表的联系,通过跟踪图象上的
点,数形结合地发现函数的图象特征和性质。
五、教学过程设计
4。 2.1 指数函数的概念
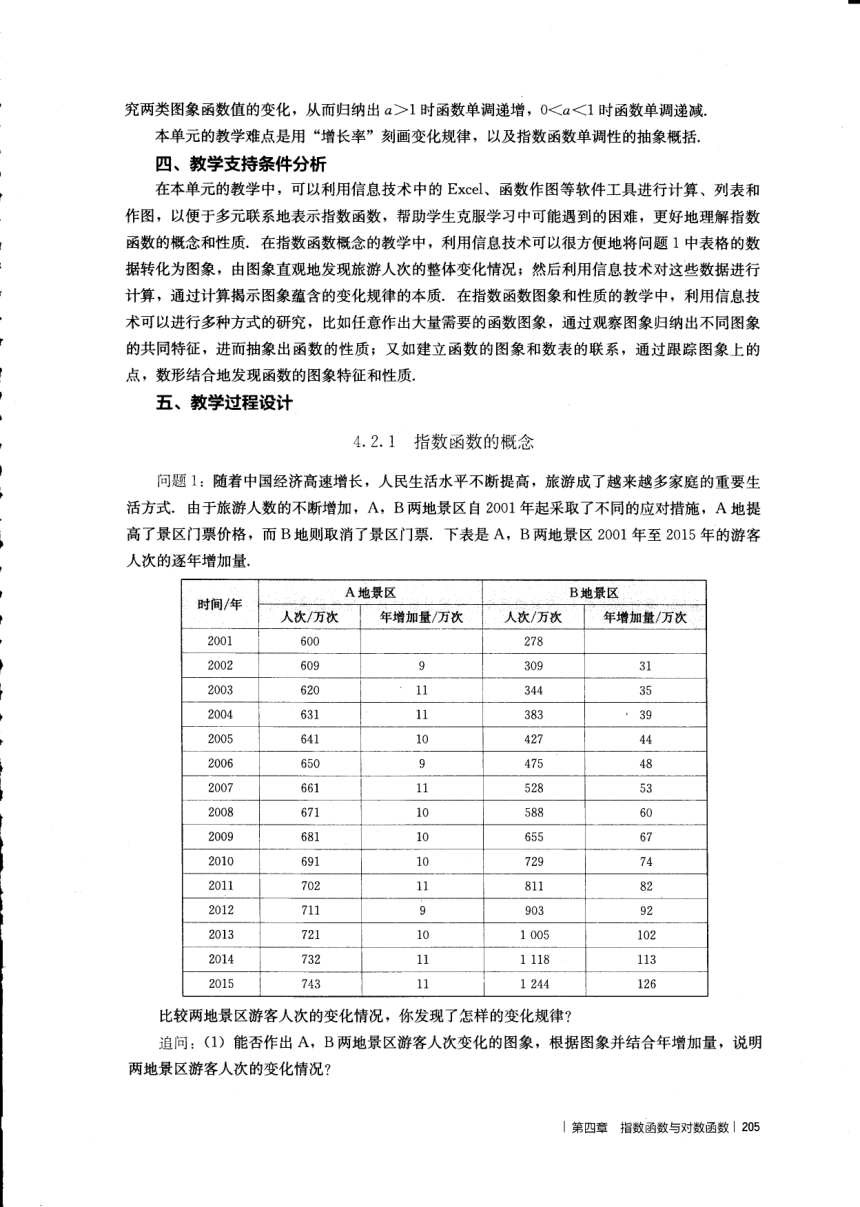
问题 1:随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生
活方式。由于旅游人数的不断增加,A,B两地景区自⒛01年起采取了不同的应对措施,A地提
高了景区门票价格,而 B地贝刂取消了景区门票。下表是 A,B两地景区 zO01年至 ⒛15年的游客
人次的逐年增加量。
比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
追问:(1)能否作出 A,B两地景区游客人次变化的图象,根据图象并结合年增加量 ,说明
两地景区游客人次的变化情况?
时阃/年 ^地
景区 B地景区
人次/万次 年增加量/万次 人次/万次 年增如蠹/万次
2001
2002 609 9 309
2005 42?
2006 650 9
588
10 729
702
9
2013 102
732 1
126
|第四章 指数函数与对数函数 |⒛5
(2)我们发现,用
“
增加量
”
不能刻画 B地景区人次的变化规律.能不能换一个量来刻画?
例如用
“
增长率
”,即从 ⒛02年起,将 B地景区每年的游客人次除以上一年的游客人次,看看能
否发现什么规律?
(3)能否求出两地景区游客人次随时间 (经过的年数)变化的函数解析式,并根据解析式说
明两地景区游客人次的变化情况?
师生活动:教师给出问题,并通过追问引导学生对问题进行分析。首先通过画出图象直观感
受 A,B两地景区游客增长的情况;为进一步刻画和比较两地游客人次的变化规律,需要通过对
相邻两年游客人次进行运算,得到 B地景区游客人次年增长率为常数,进而将其用函数 γ=
1.11:(=∈ EO,+∞))来描述。
设计意图:通过寻求 A,B两地景区游客人次增加的规律,引 出用函数刻画指数增长的问
题,为抽象出指数函数作准各。
问题 2:当生物死亡后,它机体内原有的碳 14含量会按确定的衰减比率 (简称为衰减率)衰
减,大约每经过 5730年衰减为原来的一半,这个时间称为
“
半衰期
”。按照上述变化规律,生
物体内碳 14含量与死亡年数之间有怎样的关系?
追问:(1)能否求出生物体内碳 14含量随死亡年数变化的函数解析式?
(2)生物死亡后体内碳 14含量每年衰减的比例是多少?
师生活动:教师提出问题,并让学生类比问题 1对提出的问题进行思考。通过对问题的分
析,引导学生用函数 ly=((;)5730)=臼 ∈E0,+∞))刻画碳 14衰减的规律。
设计意图:通过描述碳 14衰减的规律,引 出用函数刻画指数衰减的问题,为 抽象得到指数
函数作准备。
问题 3:比较问题 1,2中 的两个实例:B地景区游客人次增长与碳 14衰减,它们所反映的
变化规律有什么共同特征?
追问:(1)从游客人次增长和碳 14衰减的数据看,它们的变化有什么共同特征?
(2)从游客人次增长和碳 14衰减的图象看,它们的变化有什么共同特征?
(3)B地景区游客人次增长的函数解析式 丿=1.11=与 碳 14衰减的函数解析式 y=
((;)573° )z有什么共同特征?
师生活动:教师引导学生从数据、图象、解析式等角度进行归纳概括,发现刻画问题 1中的
指数增长和问题 2中的指数衰减的函数的共同特征。从解析式上来看,如果用字母 Ω代替底数
1.11和 (告
)5730,刀阝么上述函数 ly=1.11=和 ly=((告 )5730)工 就都可以表示为丿=Ω
=的形式,其
中指数£是自变量,底数 c是一个大于 0且不等于 1的常量。从而引出指数函数的概念 :
一般地,函数 y=泸 (c>0,且 四≠D口丬做指数函数,其中指数 J是自变量,定义域是 R。
在指数函数中,当 =∈ N时 ,函数 y=泸 (Ω>D还 可以表示为 y=(1+p)=,其 中p(p)0)
表示增长率;函数y=泸 (0<Ωω 表示衰减率。因此 ,
指数函数是刻画呈指数增长或指数衰减变化规律的函数模型。
设计意图:通过分析、比较两个实例,概括它们的共同本质特征,从而得到指数函数概念的
20s|普通高中教科书教师教学用书 数学 必修 第—册 |
本质属性,得 出指数函数的概念。
例 1 已知函数∫(£ )=ε r(四>0,且 n≠ D,且 ∫(3)=π ,求 ∫(0),r(1),r(-3)的 值。
师生活动:教师引导学生,要求出r(0),∫ (1),∫ (-3)的值,应先求出∫(=)=a£ 的解析
式,即先求Ω的值。而已知 r(3)=π ,可由此求出Ω的值。
设计意图:通过求函数解析式,并根据解析式求不同的函数值,从指数函数的对应关系和变
化规律的角度理解指数函数的概念.
练习 1 下列图象中,有可能表示指数函数的是 ( )。
钔 2已 知 函 数 冖 ? ∈ △ 且 “ ω 司 ,髁 吨
揣
艹 b
=℃彳? 栩 数邝 0阼獬 赋
设计意图:利 用函数的三种表示形式,从不同角度推动学生对指数函数概念的理解,进 一步
明确概念,学会表示指数函数,体会指数增长或衰减。
例 2 (1)在 问题 1中 ,如果平均每位游客出游一次可给当地带来 1000元 门票之外的收
人,A地景区的门票价格为 150元 ,比较这 15年间 A,B两地旅游收人变化情况。
(2)在问题 2中 ,某生物死亡后,过了 10000年 ,它体内碳 14的含量衰减为原来的百分
之几?
设计意图:在引入概念的两个实例基础上,利用指数函数概念进一步解决与两个实例有关的
问题,从而巩固对概念的理解。
练习 3 在某个时期,某湖泊中的蓝藻每天以 6.25%的增长率呈指数增长,那么经过 30天 ,
该湖泊的蓝藻会变为原来的多少倍?(可以使用计算工具)
设计意图:熟悉不同的指数增长的函数模型,并利用指数函数的概念解决实际问题,进 一步
巩固对概念的理解。
4。 2.P 指数函数的图象和性质
引导语:对于具体的函数,我们一般按照
“
概念—图象一性质
”
的过程进行研究。前面我们
学习了指数函数的概念,接下来就要研究它的图象和性质。回顾以往的研究经验,你能说说我们
要研究哪些内容?研究方法是什么?
师生活动:教师引导学生结合幂函数的学习,提出研究指数函数的图象和性质的内容和
方法。
设计意图:通过回顾以往研究函数图象和性质的内容和方法,提 出研究指数函数的图象和性
质的研究内容和研究方法,为接下来的学习建立先行组织者。
|第四章 指数函数与对数函数 |⒛7
问题 4:选取 a的若干值,画出指数函数 y=a=(夕 )0,且 Ω≠1)的 图象.通过观察图象的
特征可以得到一些函数的性质。你认为可以从哪些方面进行观察?你能发现函数的哪些性质?
追问:(1)观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出指
数函数 y=ε
J劬>0,且 Ω≠D的定义域、值域和单调性吗?
(2)当 色>1时 ,指数函数 y=a=的图象位置、公共点、变化趋势、定义域、值域和单调性
如何?当 0(ε (1时 ,指数函数丿=@J的情况又如何呢?
(3)比较夕)1与 0(四 (1指数函数 y=/的 图象和性质,看它们有什么区别与联系?
(4)将探索的结果填人下表 :
o(@《 1 a》 1
图 象
定义域
值 域
性 质
师生活动:教师提出问题,引导学生根据图象进行探索、思考,逐步抽象出指数函数的图象
特征和性质。在画图的过程中,可以从描点作图开始。在描点画图列函数对应值表的过程中,可
以使用计算工具,在此基础上,为了画出更多的函数的图象,帮助进行观察、归纳,可以利用信
息技术工具。由此逐渐引导学生对指数函数进行分类,得到它的单调性和特殊点的规律。
设计意图:通过画图,比较不同指数函数的图象,归纳它们的共同特征,并数形结合地抽象
出指数函数的性质。
例 3 比较下列各题中两个值的大小 :
(1) 1.725, 1.73; (2)0.8^扼 , 0.8^沔 ; (3) 1。 卩
3, o.93· 1。
师生活动:教师引导学生将每一组中的两个值可以看作一个指数函数的两个函数值,从而利
用指数函数的单调性进行比较。对于 (D(2),可 以直接利用指数函数的单调性比较;对于
(3),1.7α 3和 0.9⒊ 1不能看作某一个指数函数的两个函数值。可以利用函数丿=1.卩 和丿=0。 r
的单调性,以及
“J=0时 ,丿 =1” 这条性质把它们联系起来。
设计意图:通过应用函数的单调性比较大小,进一步理解指数函数的单调性。
练习 4 比较下列各题中两个值的大小 :
(1)6褥 ,7历 ; (2)0.3ˉ
35,0.3ˉ 2· 3; (3)1。 严5,0.512。
设计意图:通过对例题 3的 变式,促进学生对指数函数单调性的
理解。
例 4 如图,某城市人口呈指数增长。
(1)根据图象 ,估计该城市人口每翻一番所需的时间 (倍增期);
(2)该城市人口从 gO万开始,经过 zO年 ,人口会增长到多少?
(第 4题 )
而同一指数函数的师生活动:教师引导学生对问题进行分析,根据该城市人口呈指数增长 ,
20g|誓通高中教科书教师教学用书 数学 必修 第—册 |
倍增期是相同的,所以可以从图象中选取适当的点计算倍增期。要计算 ⒛ 年后的人口数,关键
是要找到 ⒛年与倍增期的数量关系,由于倍增期是 ⒛ 年,因此容易得到
“
从 ⒛ 万人开始,zo
年后人口大约会增长到 160万人
”。
设计意图:通过应用函数图象解决问题,进一步认识指数函数的图象,并 由图象理解指数函
数的概念和性质。
练习 5 在同一平面直角坐标系中画出函数丿=y和 丿=(告
)£
的图象,并说明它们的关系。
练习 6 体内癌细胞初期增加很缓慢,但到了晚期就急剧增加。试画出能大致反映体内癌细
胞数量随时间变化的草图。
设计意图:通过比较底数互为倒数的指数函数的图象,并 应用图象描述实际问题的变化规
律,进一步认识指数函数的图象,理解指数函数的概念和性质。
课堂小结
教师引导学生回顾本单元学习的主要内容,并回答下列问题 :
(1)写出一个指数函数的解析式,说明底数、增长比例和初始量的值,画出该函数的草图 ,
并说明其单调性。
(2)通过本单元的学习,你对研究函数的内容和方法有什么更进一步的认识?对比以前学习
过的一些具体函数,你能建立指数函数和它们的联系吗?请你结合下表谈谈体会.
撺数函数 △次酶数
=次
露数 夂蝴 ∷∶器轰诲髯据耄夂
解拼戎
∵∷∶焦魑
露∷0彗1
谊自Ⅱ∷∴窃良
性∷读
设计意图:结合问题 (D,教 师与学生一起回顾本单元学习的指数函数的概念、图象和性
质;结合问题 (2),建立指数函数与学习过的其他函数的联系,并进一步体会研究具体函数的内
容、过程和方法.
布置作业
根据课堂教学情况,从教科书习题 4.2中选择合适的题目。
六、目标检测设计
1.设指数函数 y=∫(J)的底数为Ω,如果∫(2)=钔 ,∫(3)=⒛ ,那么Ω= ,∫ (4)=
设计意图:考查学生对指数函数概念的理解。
2.函数 F(J)=尼Ω=(a>0,且 c≠D的 图象经过点 (0,2)和 (1,D。
(1)求该函数的解析式,并作出图象 ;
(2)判断该函数的单调性。
设计意图:考查学生对指数函数的图象和性质的掌握.
丨第四章 指数函数与对数函数 }209
-、 内容和内容解析
1.内容
本单元的知识结构如下 :
∷指数函数 :
「
ˉ? ~^ˉ ˉ?~~T— —— —~¨ ~ˉ
l
「蔽Π 「蔟l i∴哳1
本单元包括指数函数的概念、图象和性质,它们是中学数学中的重要内容。本单元共 2课
时,第 1课时的主要内容是指数函数的概念,第 2课时的主要内容是指数函数的图象和性质。
2。 内容解析
本单元是在函数的概念和性质、幂函数、指数及其运算性质的基础上,进一步研究指数函数
的概念、图象和性质。指数函数作为基本初等函数之一,是函数内容的重要组成部分;是对数函
数、等比数列、概率统计、导数等高中数学内容的基础,其思想方法与其他数学内容还有紧密的
联系;同时作为重要的函数模型还有广泛的应用,又是分析和解决大量数学问题和实际问题的重
要工具.
指数函数是一类具体的函数,有了研究幂函数的经验,便可以按研究一个函数的基本方法去
研究指数函数的主要内容.指数函数的概念体现了指数函数变量间对应关系的本质,图象和性质
则是在概念基础上进一步研究其变化规律,应该从概念出发认识图象和性质,并结合图象和性质
进一步理解概念。
指数函数是刻画呈指数增长或衰减变化规律的函数模型,其概念的教学,应该在函数概念的
基础上,重点揭示指数增长或衰减的规律:在 自变量增加 1个单位,即 自变量从£0变化到幻+1
时,相应的函数值之比
甜
=Ω 为音数,这反映了指数函数变化规律的特征。教学时要引导
学生通过实例抽象概括出这个特点,以使学生明确指数函数所刻画的现实问题的类型。
指数函数是指形如γ=α
£铴)0,且 α≠1)的函数,当 曰>1时 ,函数以指数增长;当 0(曰 (1
时,函数以指数衰减。对于指数函数图象和性质的研究,应从函数 y=Ω=(c>0,且 c≠ D出发 ,
通过Ω取不同值时函数的图象直观地体现指数函数的变化规律;然后在大量具体图象的基础上归纳
其共同特征,并选择有代表性的图象反映这样的特征,说明函数的定义域、值域、特殊点、单调
性。由函数的图象能体现函数的性质,而由函数的性质也能确定函数的图象特征,教学应突出这种
数形结合的思想方法,并通过解析式、图象、性质多元联系地认识指数函数的本质和函数模型的
特征。
|第四章 指数函数与对数函数 |203
根据上述分析,确定本单元的教学重点:指数函数的概念、图象和性质.
二、目标和目标解析
1.目标
(1)通过具体实例,了解指数函数的实际意义,理解指数函数的概念。
(2)能用描点法或借助信息技术画出具体指数函数的图象,探索并理解指数函数的单调性与
特殊点。
(3)结合指数函数概念、图象与性质的研究,进一步体会研究具体函数的一般思路和方法 ,
提升数学抽象、直观想象素养.
2.目标解析
达成上述目标的标志是 :
(1)能结合教科书中游客增长的问题 1和碳 14衰减的问题 2,通过运算发现其中具体的增长
或衰减的规律,并从中体会实际问题中变量间的关系。在了解指数函数的实际意义的基础上,知
道指数函数的含义和表示,清楚其定义域和底数Ω的取值范围。
(2)能根据函数解析式或利用计算工具计算出指数函数的两个变量的一些对应值并列表,然
后描点或利用信息技术画出指数函数的图象,或能根据函数解析式直接利用信息技术画出指数函
数的图象;结合函数图象,归纳这些图象的共同特征,探索并总结指数函数的单调性与特殊点 ,
并结合函数解析式验证所
`总
结的函数单调性和特殊点。
(3)结合指数函数的教学,体会 “概念一图象一性质”的研究具体函数的一般思路;在由具
体实例抽象为具体函数、再由具体函数概括为指数函数的过程,提升数学抽象素养;结合由函数
图象直观认识函数性质的过程,体会数形结合的思想方法,提升直观想象素养。
三、教学问题诊断分析
本单元中由具体实例抽象出指数函数的概念,不仅要能想到将问题 1游客人次的变化用图象
直观表示,还要能结合图象对已知数据进行运算后发现变化规律,并能根据问题 1和问题 2得到
的两个解析式概括出统一的函数关系式丿=aJ(厶)0,且 c≠ D。 这些对学生思维能力的要求较
高。教学中,教师要给学生探索和发现的机会,并给予学生恰当的指导.在学生不能从问题 1的
数据中发现游客人次的变化规律时,可引导学生先根据已知数据作出图象进行观察,然后启发学
生对已知数据进行运算,通过运算得到每年与上一年旅游人次的比例为常数,从而结合图象发现
变化规律的本质。这里,对数据进行哪些运算才有利于发现规律,是学生已有知识经验中缺乏
的,教学中需要引导学生注意,并注意边空中对
“
增加量
”“
增长率
”
的作用的强调.
要从不同具体问题得到的解析式概括出γ=Ω
£
的形式,可能需要指导学生将问题 2的解析式
整理为 y=((:)573°
)=·
教学中还要引导学生利用信息技术,从指数幂的意义、函数的对应关系
和图象出发,结合实例理解指数函数底数的取值范围,并在学习对数和对数函数后进一步理解。
在指数函数性质的学习过程中,尽管学生已经历过幂函数性质的学习,但那是在给定的五个
具体函数基础上进行不完整、不系统的归纳,而且幂函数性质不
“
规整
”,典型性有所欠缺,难
以完全指导其他基本初等函数的研究.指数函数性质的探索则需要学生自行选择具体的函数,必
要时教师可引导学生利用信息技术进行探索,通过画出底数 a取大量不同值时的图象,发现并归
纳函数的单调性;在探索的基础上将大量所作的图象分为增长和衰减两类,利用信息技术分别研
200|普通高中教科书教师教学用书 数学 必修 第一册 |
究两类图象函数值的变化,从而归纳出G)1时函数单调递增,0(曰 (1时函数单调递减.
本单元的教学难点是用
“
增长率
”
刻画变化规律,以及指数函数单调性的抽象概括。
四、教学支持条件分析
在本单元的教学中,可以利用信息技术中的 Exce1、 函数作图等软件工具进行计算、列表和
作图,以便于多元联系地表示指数函数,帮助学生克服学习中可能遇到的困难,更好地理解指数
函数的概念和性质。在指数函数概念的教学中,利用信息技术可以很方便地将问题 1中表格的数
据转化为图象,由 图象直观地发现旅游人次的整体变化情况;然后利用信息技术对这些数据进行
计算,通过计算揭示图象蕴含的变化规律的本质。在指数函数图象和性质的教学中,利用信息技
术可以进行多种方式的研究,比如任意作出大量需要的函数图象,通过观察图象归纳出不同图象
的共同特征,进而抽象出函数的性质;又如建立函数的图象和数表的联系,通过跟踪图象上的
点,数形结合地发现函数的图象特征和性质。
五、教学过程设计
4。 2.1 指数函数的概念
问题 1:随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生
活方式。由于旅游人数的不断增加,A,B两地景区自⒛01年起采取了不同的应对措施,A地提
高了景区门票价格,而 B地贝刂取消了景区门票。下表是 A,B两地景区 zO01年至 ⒛15年的游客
人次的逐年增加量。
比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
追问:(1)能否作出 A,B两地景区游客人次变化的图象,根据图象并结合年增加量 ,说明
两地景区游客人次的变化情况?
时阃/年 ^地
景区 B地景区
人次/万次 年增加量/万次 人次/万次 年增如蠹/万次
2001
2002 609 9 309
2005 42?
2006 650 9
588
10 729
702
9
2013 102
732 1
126
|第四章 指数函数与对数函数 |⒛5
(2)我们发现,用
“
增加量
”
不能刻画 B地景区人次的变化规律.能不能换一个量来刻画?
例如用
“
增长率
”,即从 ⒛02年起,将 B地景区每年的游客人次除以上一年的游客人次,看看能
否发现什么规律?
(3)能否求出两地景区游客人次随时间 (经过的年数)变化的函数解析式,并根据解析式说
明两地景区游客人次的变化情况?
师生活动:教师给出问题,并通过追问引导学生对问题进行分析。首先通过画出图象直观感
受 A,B两地景区游客增长的情况;为进一步刻画和比较两地游客人次的变化规律,需要通过对
相邻两年游客人次进行运算,得到 B地景区游客人次年增长率为常数,进而将其用函数 γ=
1.11:(=∈ EO,+∞))来描述。
设计意图:通过寻求 A,B两地景区游客人次增加的规律,引 出用函数刻画指数增长的问
题,为抽象出指数函数作准各。
问题 2:当生物死亡后,它机体内原有的碳 14含量会按确定的衰减比率 (简称为衰减率)衰
减,大约每经过 5730年衰减为原来的一半,这个时间称为
“
半衰期
”。按照上述变化规律,生
物体内碳 14含量与死亡年数之间有怎样的关系?
追问:(1)能否求出生物体内碳 14含量随死亡年数变化的函数解析式?
(2)生物死亡后体内碳 14含量每年衰减的比例是多少?
师生活动:教师提出问题,并让学生类比问题 1对提出的问题进行思考。通过对问题的分
析,引导学生用函数 ly=((;)5730)=臼 ∈E0,+∞))刻画碳 14衰减的规律。
设计意图:通过描述碳 14衰减的规律,引 出用函数刻画指数衰减的问题,为 抽象得到指数
函数作准备。
问题 3:比较问题 1,2中 的两个实例:B地景区游客人次增长与碳 14衰减,它们所反映的
变化规律有什么共同特征?
追问:(1)从游客人次增长和碳 14衰减的数据看,它们的变化有什么共同特征?
(2)从游客人次增长和碳 14衰减的图象看,它们的变化有什么共同特征?
(3)B地景区游客人次增长的函数解析式 丿=1.11=与 碳 14衰减的函数解析式 y=
((;)573° )z有什么共同特征?
师生活动:教师引导学生从数据、图象、解析式等角度进行归纳概括,发现刻画问题 1中的
指数增长和问题 2中的指数衰减的函数的共同特征。从解析式上来看,如果用字母 Ω代替底数
1.11和 (告
)5730,刀阝么上述函数 ly=1.11=和 ly=((告 )5730)工 就都可以表示为丿=Ω
=的形式,其
中指数£是自变量,底数 c是一个大于 0且不等于 1的常量。从而引出指数函数的概念 :
一般地,函数 y=泸 (c>0,且 四≠D口丬做指数函数,其中指数 J是自变量,定义域是 R。
在指数函数中,当 =∈ N时 ,函数 y=泸 (Ω>D还 可以表示为 y=(1+p)=,其 中p(p)0)
表示增长率;函数y=泸 (0<Ω
指数函数是刻画呈指数增长或指数衰减变化规律的函数模型。
设计意图:通过分析、比较两个实例,概括它们的共同本质特征,从而得到指数函数概念的
20s|普通高中教科书教师教学用书 数学 必修 第—册 |
本质属性,得 出指数函数的概念。
例 1 已知函数∫(£ )=ε r(四>0,且 n≠ D,且 ∫(3)=π ,求 ∫(0),r(1),r(-3)的 值。
师生活动:教师引导学生,要求出r(0),∫ (1),∫ (-3)的值,应先求出∫(=)=a£ 的解析
式,即先求Ω的值。而已知 r(3)=π ,可由此求出Ω的值。
设计意图:通过求函数解析式,并根据解析式求不同的函数值,从指数函数的对应关系和变
化规律的角度理解指数函数的概念.
练习 1 下列图象中,有可能表示指数函数的是 ( )。
钔 2已 知 函 数 冖 ? ∈ △ 且 “ ω 司 ,髁 吨
揣
艹 b
=℃彳? 栩 数邝 0阼獬 赋
设计意图:利 用函数的三种表示形式,从不同角度推动学生对指数函数概念的理解,进 一步
明确概念,学会表示指数函数,体会指数增长或衰减。
例 2 (1)在 问题 1中 ,如果平均每位游客出游一次可给当地带来 1000元 门票之外的收
人,A地景区的门票价格为 150元 ,比较这 15年间 A,B两地旅游收人变化情况。
(2)在问题 2中 ,某生物死亡后,过了 10000年 ,它体内碳 14的含量衰减为原来的百分
之几?
设计意图:在引入概念的两个实例基础上,利用指数函数概念进一步解决与两个实例有关的
问题,从而巩固对概念的理解。
练习 3 在某个时期,某湖泊中的蓝藻每天以 6.25%的增长率呈指数增长,那么经过 30天 ,
该湖泊的蓝藻会变为原来的多少倍?(可以使用计算工具)
设计意图:熟悉不同的指数增长的函数模型,并利用指数函数的概念解决实际问题,进 一步
巩固对概念的理解。
4。 2.P 指数函数的图象和性质
引导语:对于具体的函数,我们一般按照
“
概念—图象一性质
”
的过程进行研究。前面我们
学习了指数函数的概念,接下来就要研究它的图象和性质。回顾以往的研究经验,你能说说我们
要研究哪些内容?研究方法是什么?
师生活动:教师引导学生结合幂函数的学习,提出研究指数函数的图象和性质的内容和
方法。
设计意图:通过回顾以往研究函数图象和性质的内容和方法,提 出研究指数函数的图象和性
质的研究内容和研究方法,为接下来的学习建立先行组织者。
|第四章 指数函数与对数函数 |⒛7
问题 4:选取 a的若干值,画出指数函数 y=a=(夕 )0,且 Ω≠1)的 图象.通过观察图象的
特征可以得到一些函数的性质。你认为可以从哪些方面进行观察?你能发现函数的哪些性质?
追问:(1)观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出指
数函数 y=ε
J劬>0,且 Ω≠D的定义域、值域和单调性吗?
(2)当 色>1时 ,指数函数 y=a=的图象位置、公共点、变化趋势、定义域、值域和单调性
如何?当 0(ε (1时 ,指数函数丿=@J的情况又如何呢?
(3)比较夕)1与 0(四 (1指数函数 y=/的 图象和性质,看它们有什么区别与联系?
(4)将探索的结果填人下表 :
o(@《 1 a》 1
图 象
定义域
值 域
性 质
师生活动:教师提出问题,引导学生根据图象进行探索、思考,逐步抽象出指数函数的图象
特征和性质。在画图的过程中,可以从描点作图开始。在描点画图列函数对应值表的过程中,可
以使用计算工具,在此基础上,为了画出更多的函数的图象,帮助进行观察、归纳,可以利用信
息技术工具。由此逐渐引导学生对指数函数进行分类,得到它的单调性和特殊点的规律。
设计意图:通过画图,比较不同指数函数的图象,归纳它们的共同特征,并数形结合地抽象
出指数函数的性质。
例 3 比较下列各题中两个值的大小 :
(1) 1.725, 1.73; (2)0.8^扼 , 0.8^沔 ; (3) 1。 卩
3, o.93· 1。
师生活动:教师引导学生将每一组中的两个值可以看作一个指数函数的两个函数值,从而利
用指数函数的单调性进行比较。对于 (D(2),可 以直接利用指数函数的单调性比较;对于
(3),1.7α 3和 0.9⒊ 1不能看作某一个指数函数的两个函数值。可以利用函数丿=1.卩 和丿=0。 r
的单调性,以及
“J=0时 ,丿 =1” 这条性质把它们联系起来。
设计意图:通过应用函数的单调性比较大小,进一步理解指数函数的单调性。
练习 4 比较下列各题中两个值的大小 :
(1)6褥 ,7历 ; (2)0.3ˉ
35,0.3ˉ 2· 3; (3)1。 严5,0.512。
设计意图:通过对例题 3的 变式,促进学生对指数函数单调性的
理解。
例 4 如图,某城市人口呈指数增长。
(1)根据图象 ,估计该城市人口每翻一番所需的时间 (倍增期);
(2)该城市人口从 gO万开始,经过 zO年 ,人口会增长到多少?
(第 4题 )
而同一指数函数的师生活动:教师引导学生对问题进行分析,根据该城市人口呈指数增长 ,
20g|誓通高中教科书教师教学用书 数学 必修 第—册 |
倍增期是相同的,所以可以从图象中选取适当的点计算倍增期。要计算 ⒛ 年后的人口数,关键
是要找到 ⒛年与倍增期的数量关系,由于倍增期是 ⒛ 年,因此容易得到
“
从 ⒛ 万人开始,zo
年后人口大约会增长到 160万人
”。
设计意图:通过应用函数图象解决问题,进一步认识指数函数的图象,并 由图象理解指数函
数的概念和性质。
练习 5 在同一平面直角坐标系中画出函数丿=y和 丿=(告
)£
的图象,并说明它们的关系。
练习 6 体内癌细胞初期增加很缓慢,但到了晚期就急剧增加。试画出能大致反映体内癌细
胞数量随时间变化的草图。
设计意图:通过比较底数互为倒数的指数函数的图象,并 应用图象描述实际问题的变化规
律,进一步认识指数函数的图象,理解指数函数的概念和性质。
课堂小结
教师引导学生回顾本单元学习的主要内容,并回答下列问题 :
(1)写出一个指数函数的解析式,说明底数、增长比例和初始量的值,画出该函数的草图 ,
并说明其单调性。
(2)通过本单元的学习,你对研究函数的内容和方法有什么更进一步的认识?对比以前学习
过的一些具体函数,你能建立指数函数和它们的联系吗?请你结合下表谈谈体会.
撺数函数 △次酶数
=次
露数 夂蝴 ∷∶器轰诲髯据耄夂
解拼戎
∵∷∶焦魑
露∷0彗1
谊自Ⅱ∷∴窃良
性∷读
设计意图:结合问题 (D,教 师与学生一起回顾本单元学习的指数函数的概念、图象和性
质;结合问题 (2),建立指数函数与学习过的其他函数的联系,并进一步体会研究具体函数的内
容、过程和方法.
布置作业
根据课堂教学情况,从教科书习题 4.2中选择合适的题目。
六、目标检测设计
1.设指数函数 y=∫(J)的底数为Ω,如果∫(2)=钔 ,∫(3)=⒛ ,那么Ω= ,∫ (4)=
设计意图:考查学生对指数函数概念的理解。
2.函数 F(J)=尼Ω=(a>0,且 c≠D的 图象经过点 (0,2)和 (1,D。
(1)求该函数的解析式,并作出图象 ;
(2)判断该函数的单调性。
设计意图:考查学生对指数函数的图象和性质的掌握.
丨第四章 指数函数与对数函数 }209
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
