1.1.1 任意角 课件 19张PPT
图片预览






文档简介
(共19张PPT)
任意角
问题情境:
在体操、跳水中,有“转体720°”、“翻腾两周半”这样的动作名称,“720°”在这里也是用来表示旋转程度的一个角。请问“720°”是怎样的一个角?
问题情境:
自主导学:
1、你认为在本节中涉及到了哪些新的数学概念?
2、请你指出角30°、120°、240°、330°终边所在的象限。
3、-300°,-150°,-60°,60°,210°,300°,420°角分别是第几象限角?其中哪些角的终边相同?
4、具有相同终边的角彼此之间有什么关系?你能写出与60°角终边相同的角的集合吗?
请带着这些问题自学课本5-6页。
1、你认为在本节中涉及到了哪些新的数学概念?
自主导学:
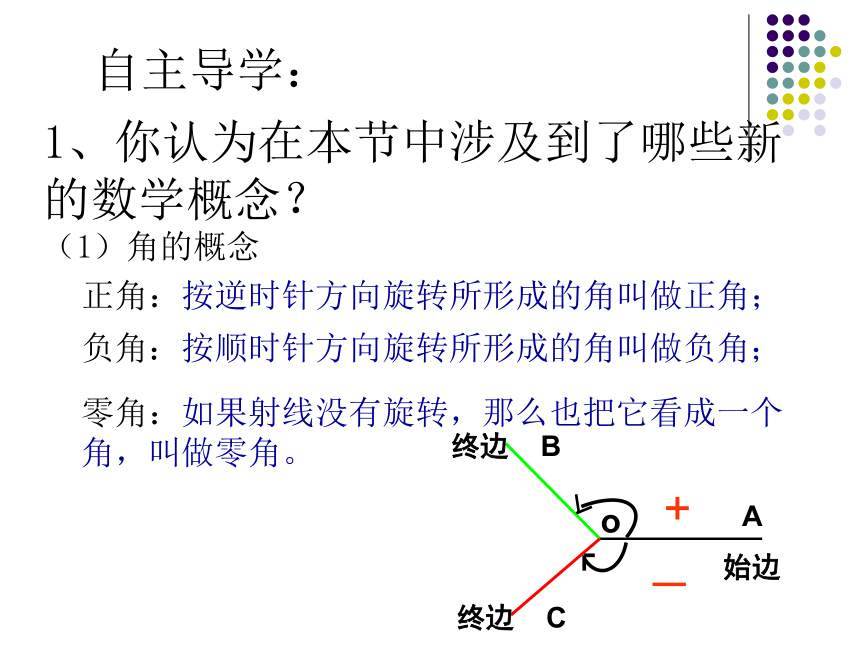
正角:按逆时针方向旋转所形成的角叫做正角;
负角:按顺时针方向旋转所形成的角叫做负角;
零角:如果射线没有旋转,那么也把它看成一个角,叫做零角。
A
始边
终边 B
终边 C
o
+
—
(1)角的概念
1、你认为在本节中涉及到了哪些新的数学概念?
(2)象限角:角的终边(除端点外)在第几象限就说这个角是第几象限角。
1)角的顶点与原点重合;
2)角的始边与x轴的非负半轴重合.
规定:
(3)终边相同角
初中
高中
及时测评:
1、始边和终边重合的角一定是零角吗?
2、锐角是第一象限角吗?第一象限角一定是锐角吗?
2、请你指出角30°、120°、240°、330°终边所在的象限。
3、-300°,-150°,-60°,60°,210°,300°,420°角分别是第几象限角?其中哪些角的终边相同?
4、具有相同终边的角彼此之间有什么关系?你能写出与60°角终边相同的角的集合吗?
若将60°换成α角呢?
与?终边相同的角的一般形式为
{β| β= k·360? +?,k∈Z}
注: (1) K ∈ Z
(2) ? 是任意角
(3)K·360°与 ?之间是“+”号,如K·360°-30 °,应看成K·360 °+(-30 ° )
(4)终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数多个,它们相差360°的整数倍。
例1、 在0°到360°的范围内,找出与下列各角终边相同的角,并分别判断它们是第几象限角:
(1)650°(2)-150°(3) -990°15′
解(1)因为650°=360°+290°
所以650°的角与290°角终边相同,是第四象限角。
(2)-150°=-360°+210°
所以-150°的角与210°的角终边相同,是第三象限角。
(3)-990°15′ = -3×360°+89°45′
所以-990°15′的角与89°45′的角终边相同,是第一象限角。
总结例1的求解方法。
及时测评:
在0°到360°的范围内,找出与下列各角终边相同的角,并判断它们是第几象限角:
(1)-50°(2)390 °5′ (3) 1935°
收获总结:
1、数形结合
3、终边相同角。
本节课涉及到的知识和方法主要有
知识点:
1、正角、负角、零角;
2、象限角;
思想方法:
2、化归转化
课后思考:写出终边落在x轴上的角的集合.
课时作业:课本P7,练习T4,5。
感谢各位评委莅临指导
例2、已知α与240°角的终边相同,判断α/2是第几象限角。
变式训练:已知α与240°角的终边相同,判断2α是第几象限角。
2α=2k?360?+480?
=(2k+1)?360?+120?,k?Z
所以2α是第二象限角
解
1.已知下列各角:①-120°;②-240°;③180°;
④495°,其中是第二象限角的是____ 。
2.若β是第四象限角,则180°+β是第____象限角.
二
②④
课后思考:写出终边落在x轴上的角的集合.
解:在0°~360°范围内,终边在x轴上的角有两个0°,180°.
S1={β| β=k×360°, k∈Z };
与180°角终边相同的角构成的集合
S2={β| β=180°+k×360°,k∈Z }
={β| β=180°+2k×180°,k∈Z }.
与0°角终边相同的角构成的集合
S=S1∪S2
={β|β=k×180°, k∈Z }.
任意角
问题情境:
在体操、跳水中,有“转体720°”、“翻腾两周半”这样的动作名称,“720°”在这里也是用来表示旋转程度的一个角。请问“720°”是怎样的一个角?
问题情境:
自主导学:
1、你认为在本节中涉及到了哪些新的数学概念?
2、请你指出角30°、120°、240°、330°终边所在的象限。
3、-300°,-150°,-60°,60°,210°,300°,420°角分别是第几象限角?其中哪些角的终边相同?
4、具有相同终边的角彼此之间有什么关系?你能写出与60°角终边相同的角的集合吗?
请带着这些问题自学课本5-6页。
1、你认为在本节中涉及到了哪些新的数学概念?
自主导学:
正角:按逆时针方向旋转所形成的角叫做正角;
负角:按顺时针方向旋转所形成的角叫做负角;
零角:如果射线没有旋转,那么也把它看成一个角,叫做零角。
A
始边
终边 B
终边 C
o
+
—
(1)角的概念
1、你认为在本节中涉及到了哪些新的数学概念?
(2)象限角:角的终边(除端点外)在第几象限就说这个角是第几象限角。
1)角的顶点与原点重合;
2)角的始边与x轴的非负半轴重合.
规定:
(3)终边相同角
初中
高中
及时测评:
1、始边和终边重合的角一定是零角吗?
2、锐角是第一象限角吗?第一象限角一定是锐角吗?
2、请你指出角30°、120°、240°、330°终边所在的象限。
3、-300°,-150°,-60°,60°,210°,300°,420°角分别是第几象限角?其中哪些角的终边相同?
4、具有相同终边的角彼此之间有什么关系?你能写出与60°角终边相同的角的集合吗?
若将60°换成α角呢?
与?终边相同的角的一般形式为
{β| β= k·360? +?,k∈Z}
注: (1) K ∈ Z
(2) ? 是任意角
(3)K·360°与 ?之间是“+”号,如K·360°-30 °,应看成K·360 °+(-30 ° )
(4)终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数多个,它们相差360°的整数倍。
例1、 在0°到360°的范围内,找出与下列各角终边相同的角,并分别判断它们是第几象限角:
(1)650°(2)-150°(3) -990°15′
解(1)因为650°=360°+290°
所以650°的角与290°角终边相同,是第四象限角。
(2)-150°=-360°+210°
所以-150°的角与210°的角终边相同,是第三象限角。
(3)-990°15′ = -3×360°+89°45′
所以-990°15′的角与89°45′的角终边相同,是第一象限角。
总结例1的求解方法。
及时测评:
在0°到360°的范围内,找出与下列各角终边相同的角,并判断它们是第几象限角:
(1)-50°(2)390 °5′ (3) 1935°
收获总结:
1、数形结合
3、终边相同角。
本节课涉及到的知识和方法主要有
知识点:
1、正角、负角、零角;
2、象限角;
思想方法:
2、化归转化
课后思考:写出终边落在x轴上的角的集合.
课时作业:课本P7,练习T4,5。
感谢各位评委莅临指导
例2、已知α与240°角的终边相同,判断α/2是第几象限角。
变式训练:已知α与240°角的终边相同,判断2α是第几象限角。
2α=2k?360?+480?
=(2k+1)?360?+120?,k?Z
所以2α是第二象限角
解
1.已知下列各角:①-120°;②-240°;③180°;
④495°,其中是第二象限角的是____ 。
2.若β是第四象限角,则180°+β是第____象限角.
二
②④
课后思考:写出终边落在x轴上的角的集合.
解:在0°~360°范围内,终边在x轴上的角有两个0°,180°.
S1={β| β=k×360°, k∈Z };
与180°角终边相同的角构成的集合
S2={β| β=180°+k×360°,k∈Z }
={β| β=180°+2k×180°,k∈Z }.
与0°角终边相同的角构成的集合
S=S1∪S2
={β|β=k×180°, k∈Z }.
