1.2.3 三角函数的诱导公式 课件(共22张PPT)
文档属性
| 名称 | 1.2.3 三角函数的诱导公式 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 23:42:10 | ||
图片预览






文档简介
(共22张PPT)
我没有什么特别的才能,不过是喜欢寻根刨底的探究问题罢了。
——爱因斯坦
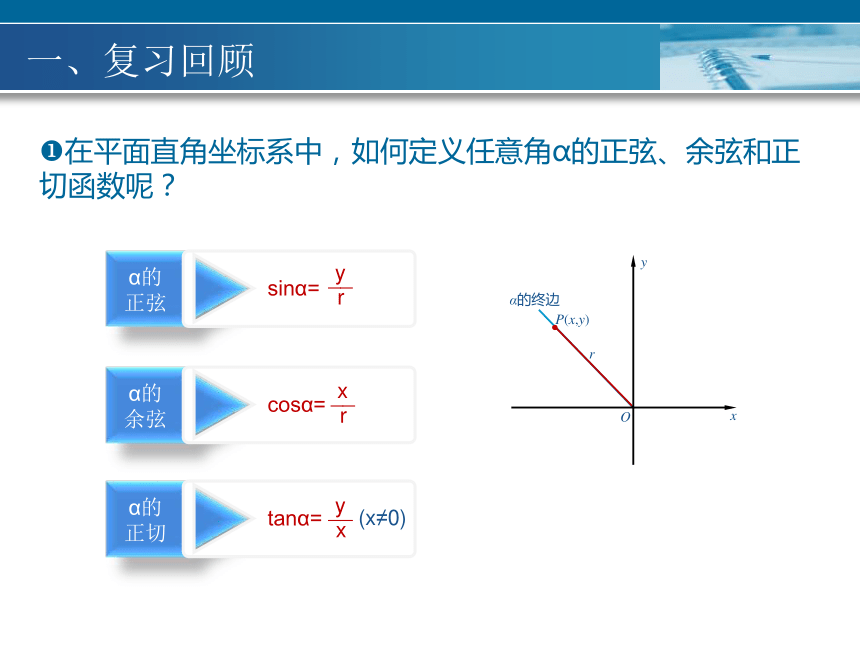
?在平面直角坐标系中,如何定义任意角α的正弦、余弦和正切函数呢?
P(x,y)
一、复习回顾
O
x
y
α的终边
r
(x≠0)
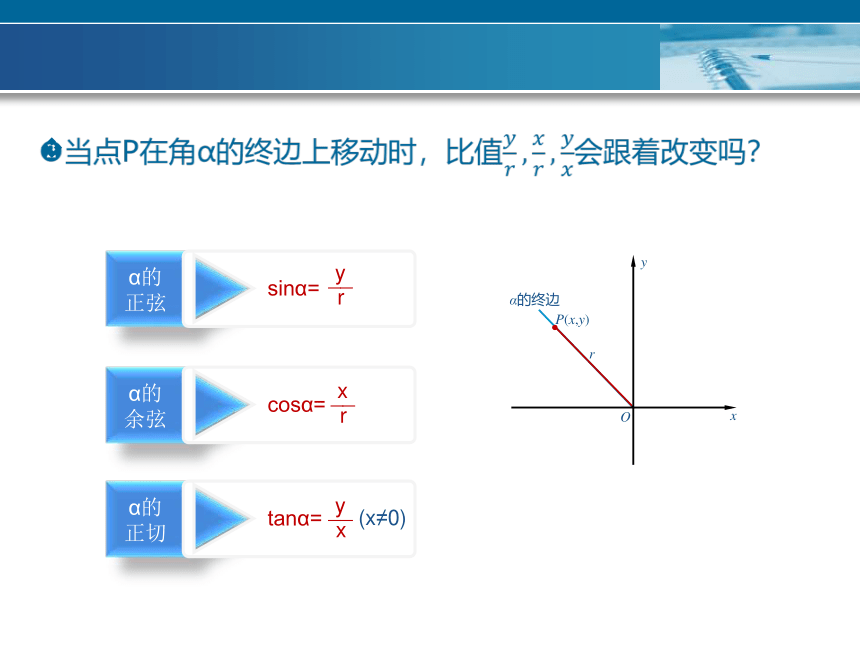
P(x,y)
O
x
y
α的终边
r
(x≠0)
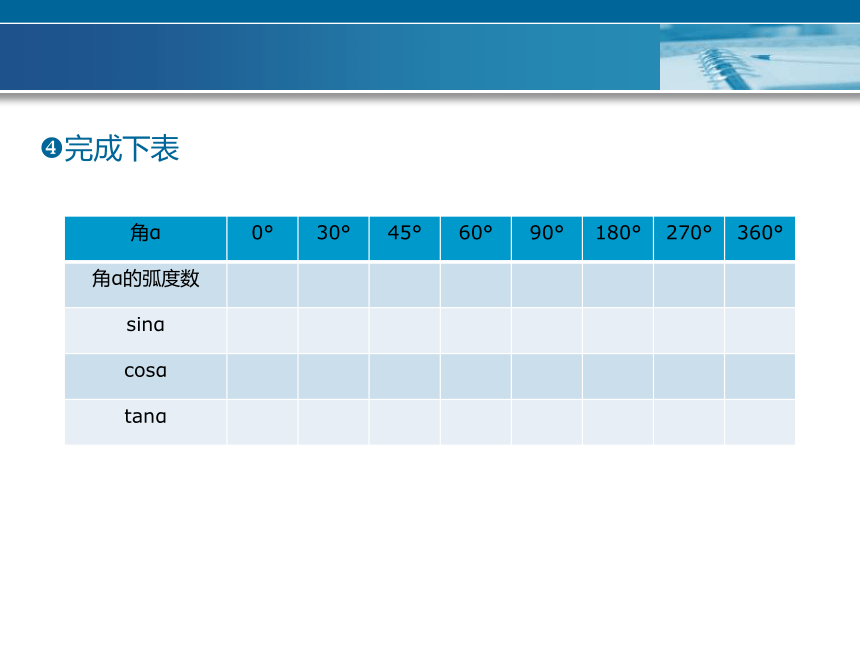
?完成下表
角α 0° 30° 45° 60° 90° 180° 270° 360°
角α的弧度数
sinα
cosα
tanα
?如何选择合适的点P,能够有效地研究任意角α的正弦、余弦和正切值呢?
二、问题情境
P(cosα,sinα)
O
x
y
α的终边
1
事实上,对于图形的对称性,其本质是这样的:如图所示,说圆O关于AB对称,是指在圆O上任取一点P,它关于AB对称的点P'也一定在圆O上,所以图形的对称性可归结为点的对称性。
如果点P 恰好在点A 处, 那么它关于AB对称的点P’在哪儿呢?
如何用代数式子来刻画这种几何图形上的对称关系呢?
?对于公式一
cos(α+2kπ)=cosα
sin(α+2kπ)=sinα (k∈Z)
tan(α+2kπ)=tanα
【思考1】能用一句话概括这一组公式吗?
终边相同的角三角函数值相同.
【思考2】能用一句话说明这组公式的作用吗?
将任意角的三角函数值转化为(0,2π)内角的三角函数值.
苏教版数学必修4第1章1.2.3
第一课时
思考 这个公式可以得到三角函数的什么性质?
三、建构数学:三角函数的诱导公式
公式的导出
请大家反思一下我们是如何推出这些公式的?
问题反思
如何来记忆这组公式呢?
对称关系
诱导公式
坐标关系 两角关系
?
?
?
识记方法
三角函数的诱导公式
sinα
cosα
tanα
sinα
-cosα
-tanα
-sinα
cosα
-tanα
-sinα
-cosα
tanα
四、数学运用
例1 求值:
小结一下
求任意角的三角函数值的步骤:
任意负角的三角函数
一个正角的三角函数
0~2π间角的三角函数
锐角的三角函数
例2 判断下列函数的奇偶性:
(1)f(x)=1-cosx ; (2)g(x)=x-sinx.
五、小结与反思
知识结构
探究途径
拓展反思
练习与巩固
练习 求值:书本P20页
练习与巩固
练习 判断下列函数的奇偶性(书本P20页)
例3 化简:
化简:
变式1
变式2
变式3
(n∈Z)
练习与巩固
我没有什么特别的才能,不过是喜欢寻根刨底的探究问题罢了。
——爱因斯坦
?在平面直角坐标系中,如何定义任意角α的正弦、余弦和正切函数呢?
P(x,y)
一、复习回顾
O
x
y
α的终边
r
(x≠0)
P(x,y)
O
x
y
α的终边
r
(x≠0)
?完成下表
角α 0° 30° 45° 60° 90° 180° 270° 360°
角α的弧度数
sinα
cosα
tanα
?如何选择合适的点P,能够有效地研究任意角α的正弦、余弦和正切值呢?
二、问题情境
P(cosα,sinα)
O
x
y
α的终边
1
事实上,对于图形的对称性,其本质是这样的:如图所示,说圆O关于AB对称,是指在圆O上任取一点P,它关于AB对称的点P'也一定在圆O上,所以图形的对称性可归结为点的对称性。
如果点P 恰好在点A 处, 那么它关于AB对称的点P’在哪儿呢?
如何用代数式子来刻画这种几何图形上的对称关系呢?
?对于公式一
cos(α+2kπ)=cosα
sin(α+2kπ)=sinα (k∈Z)
tan(α+2kπ)=tanα
【思考1】能用一句话概括这一组公式吗?
终边相同的角三角函数值相同.
【思考2】能用一句话说明这组公式的作用吗?
将任意角的三角函数值转化为(0,2π)内角的三角函数值.
苏教版数学必修4第1章1.2.3
第一课时
思考 这个公式可以得到三角函数的什么性质?
三、建构数学:三角函数的诱导公式
公式的导出
请大家反思一下我们是如何推出这些公式的?
问题反思
如何来记忆这组公式呢?
对称关系
诱导公式
坐标关系 两角关系
?
?
?
识记方法
三角函数的诱导公式
sinα
cosα
tanα
sinα
-cosα
-tanα
-sinα
cosα
-tanα
-sinα
-cosα
tanα
四、数学运用
例1 求值:
小结一下
求任意角的三角函数值的步骤:
任意负角的三角函数
一个正角的三角函数
0~2π间角的三角函数
锐角的三角函数
例2 判断下列函数的奇偶性:
(1)f(x)=1-cosx ; (2)g(x)=x-sinx.
五、小结与反思
知识结构
探究途径
拓展反思
练习与巩固
练习 求值:书本P20页
练习与巩固
练习 判断下列函数的奇偶性(书本P20页)
例3 化简:
化简:
变式1
变式2
变式3
(n∈Z)
练习与巩固
