1.2.3 三角函数的诱导公式
图片预览






文档简介
(共24张PPT)
第一章 三角函数
1.2.3.三角函数的诱导公式
一、课前预热
1.任意角α的正弦、
余弦、正切是怎样
定义的?
一、课前预热
二、导入新课
互动:(抢答)
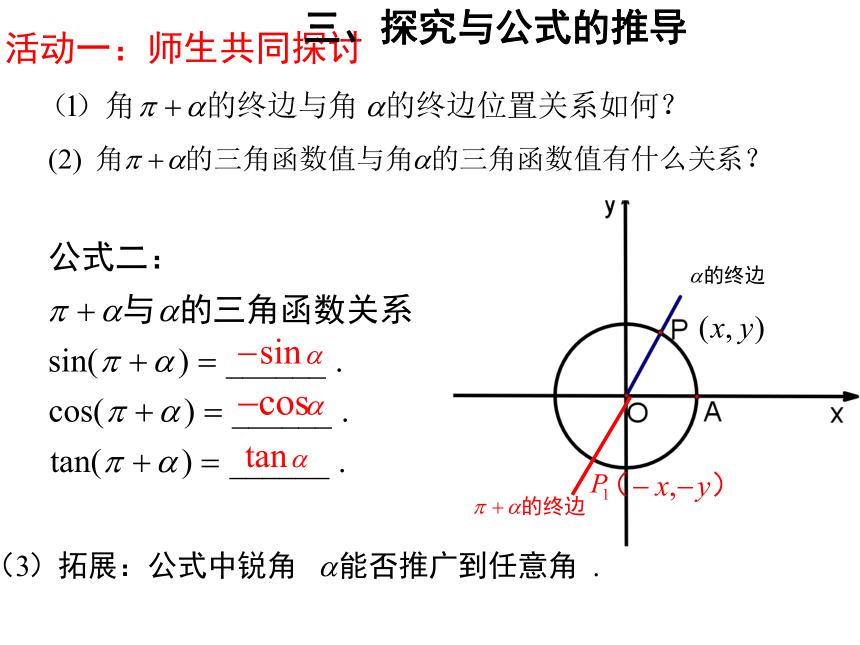
三、探究与公式的推导
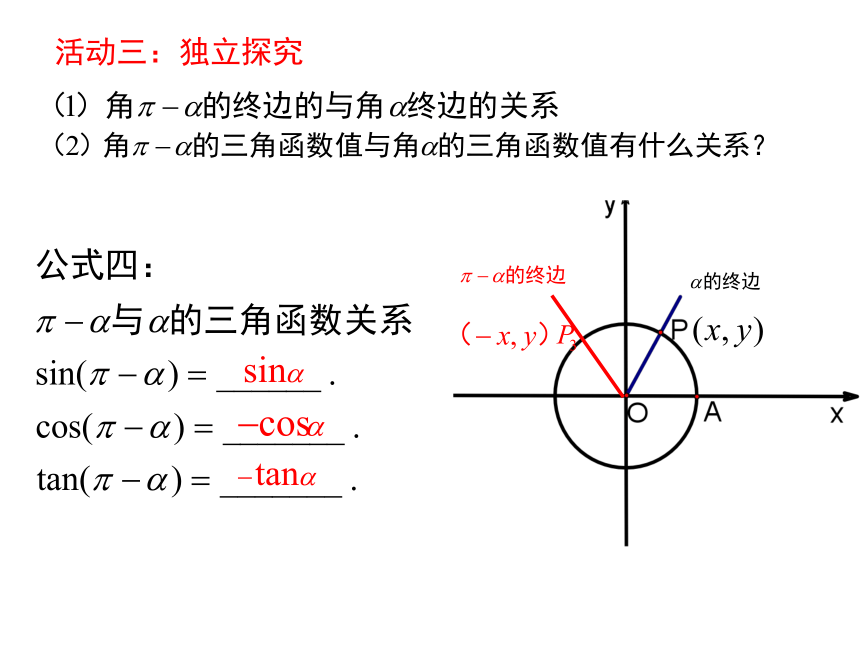
思考3:结合公式二、三,你能推出公式四吗?
公式二:
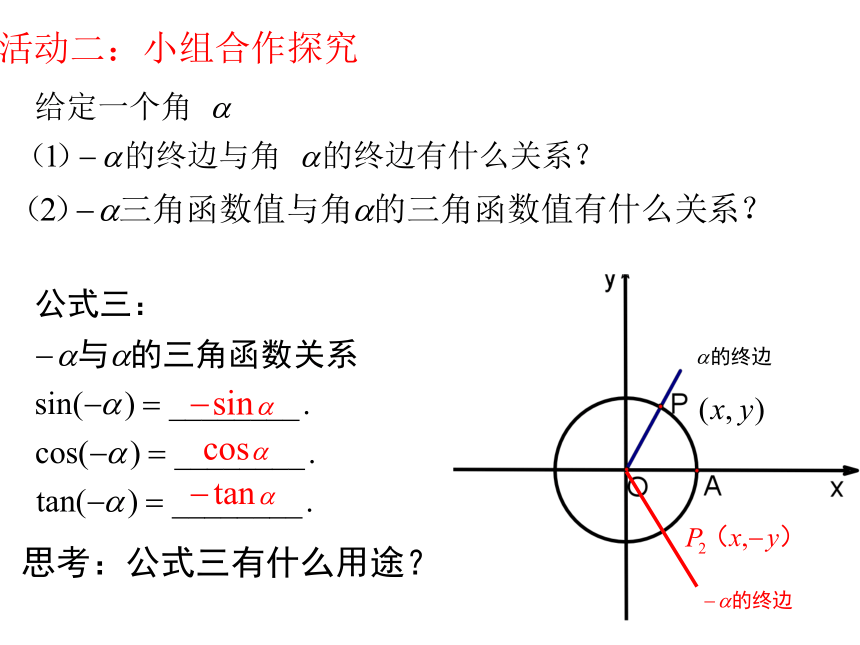
公式三:
公式四:
公式一:
大化小
负化正
公式一~四小结
四、示例应用
利用诱导公式把任意角的三角函数转化为锐角三角
函数,一般按下面步骤进行:
任意负角的
三角函数
任意正角的
三角函数
0~2∏的角
的三角函数
根据练习你来归纳总结:
锐角三
角函数
求值
把任意角的三角函数转化为锐角三角函数的步骤有哪些?
负化正,大化小,化到锐角为终了
例题讲解
理论迁移
例题讲解
理论迁移
特别提示:符号问题
1、化任意角的三角函数为锐角三角函数的一般思路为:
小结
上述过程体现了由未知到已知的化归思想。“负化正,大化小,化到锐角为终了”。
作业布置:课本29页习题
敬请指导
敬请指导
变式
已知cos(π+x)
求
下列各式的值:
(1)cos(2丌-x);(2)cos(π-x
公式
sin(+2k)=sna(k∈Z)
COs(a+2k)=c0Sa(k∈Z)
tan(x+2kx)=ana(k∈Z)
公式二
sin(+a=sin a
cos(兀+c)=-cosC
tan(T +a)=tan a
2.在我们探究公式的过程中,主要运用了
哪些策略与方法?
数形
由特殊先猜想
结合
到一般再证明
第一章 三角函数
1.2.3.三角函数的诱导公式
一、课前预热
1.任意角α的正弦、
余弦、正切是怎样
定义的?
一、课前预热
二、导入新课
互动:(抢答)
三、探究与公式的推导
思考3:结合公式二、三,你能推出公式四吗?
公式二:
公式三:
公式四:
公式一:
大化小
负化正
公式一~四小结
四、示例应用
利用诱导公式把任意角的三角函数转化为锐角三角
函数,一般按下面步骤进行:
任意负角的
三角函数
任意正角的
三角函数
0~2∏的角
的三角函数
根据练习你来归纳总结:
锐角三
角函数
求值
把任意角的三角函数转化为锐角三角函数的步骤有哪些?
负化正,大化小,化到锐角为终了
例题讲解
理论迁移
例题讲解
理论迁移
特别提示:符号问题
1、化任意角的三角函数为锐角三角函数的一般思路为:
小结
上述过程体现了由未知到已知的化归思想。“负化正,大化小,化到锐角为终了”。
作业布置:课本29页习题
敬请指导
敬请指导
变式
已知cos(π+x)
求
下列各式的值:
(1)cos(2丌-x);(2)cos(π-x
公式
sin(+2k)=sna(k∈Z)
COs(a+2k)=c0Sa(k∈Z)
tan(x+2kx)=ana(k∈Z)
公式二
sin(+a=sin a
cos(兀+c)=-cosC
tan(T +a)=tan a
2.在我们探究公式的过程中,主要运用了
哪些策略与方法?
数形
由特殊先猜想
结合
到一般再证明
