北师大版七年级数学下册课件5.3简单的轴对称图形(26张PPT)
文档属性
| 名称 | 北师大版七年级数学下册课件5.3简单的轴对称图形(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 318.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览







文档简介
课件26张PPT。3 简单的轴对称图形第五章 生活中的轴对称北师版
七年级
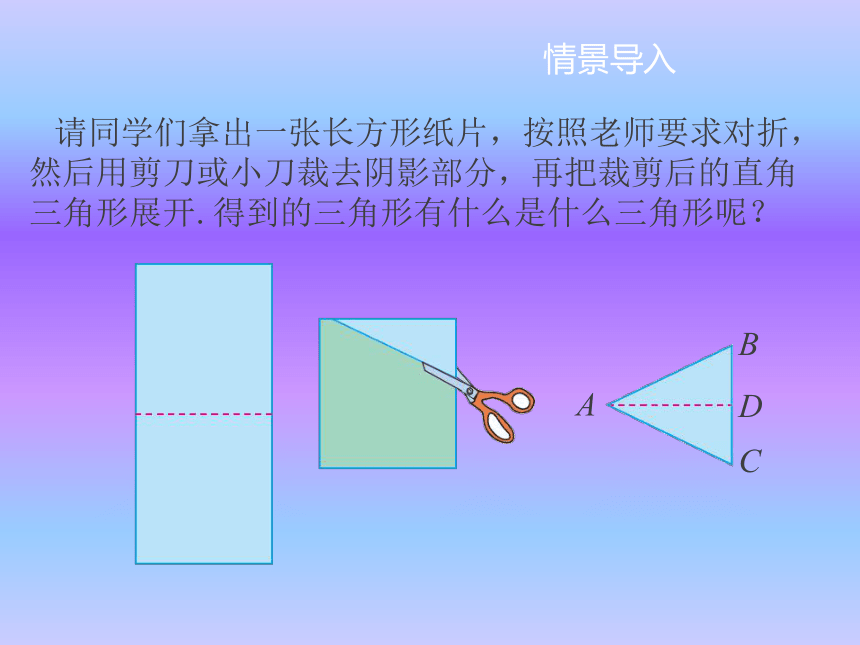
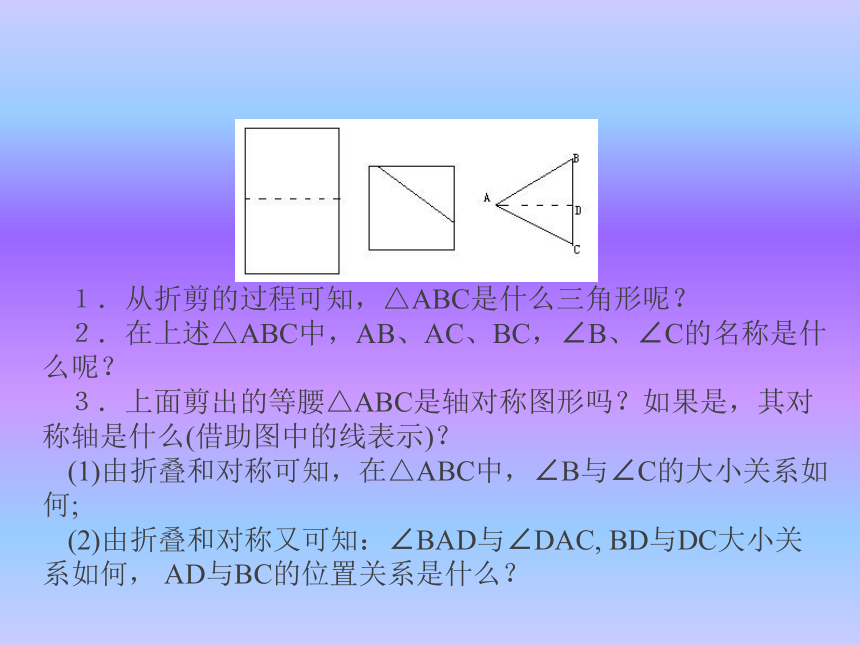
下册请同学们拿出一张长方形纸片,按照老师要求对折,然后用剪刀或小刀裁去阴影部分,再把裁剪后的直角三角形展开.得到的三角形有什么是什么三角形呢?情景导入1.从折剪的过程可知,△ABC是什么三角形呢?
2.在上述△ABC中,AB、AC、BC,∠B、∠C的名称是什么呢?
3.上面剪出的等腰△ABC是轴对称图形吗?如果是,其对称轴是什么(借助图中的线表示)?
(1)由折叠和对称可知,在△ABC中,∠B与∠C的大小关系如何;
(2)由折叠和对称又可知:∠BAD与∠DAC, BD与DC大小关系如何, AD与BC的位置关系是什么?1.掌握等腰三角形的性质,体会数学中的转化思想;
2.能运用等腰三角形的性质进行证明和计算.
学习目标 利用实验操作的方法,我们发现并概括出等腰三角
形的性质1和性质2.对于性质1,你能通过严格的逻辑
推理证明这个结论吗?
(1)你能根据结论画出图形,写出已知、求证吗?
(2)结合所画的图形,你认为证明两个底角相等的思
路是什么?
(3)如何在一个等腰三角形中构造出两个全等三角形
呢?从剪图、折纸的过程中你能获得什么启发? 探究点一 等腰三角形性质讲授新课 已知:如图,△ABC 中,AB =AC.求证:∠B =
∠C. 证明:作底边的中线AD.
∵ AB =AC,
BD =CD,
AD =AD,
∴ △ABD ≌△ACD(SSS).
∴ ∠B =∠C.证明等腰三角形的性质 你还有其他方法证明性质1吗?证明等腰三角形的性质 可以作底边的高线或顶角的角平分线. 性质2可以分解为三个命题,本节课证明“等腰三
角形的底边上的中线也是底边上的高和顶角平分线”. 已知:如图,△ABC 中,AB =AC,AD 是底边BC
的中线.求证:∠BAD =∠CAD,AD⊥BC.证明等腰三角形的性质 证明:∵ AD 是底边BC 的中线,
∴ BD =CD.
∵ AB =AC,
BD =CD,
AD =AD,
∴ △ABD ≌△ACD(SSS).证明等腰三角形的性质 已知:如图,△ABC 中,AB =AC,AD 是底边BC
的中线.求证:∠BAD =∠CAD,AD⊥BC. 证明:∴ ∠BAD =∠CAD,
∠ADB =∠ADC.
∵ ∠ADB +∠ADC =180°,
∴ ∠ADB =90°.
∴ AD⊥BC.探索并证明等腰三角形的性质 在等腰三角形性质的探索过程和证明过程中,“折
痕”“辅助线”发挥了非常重要的作用,由此,你能发
现等腰三角形具有什么特征?
等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴.课堂练习 练习1 填空:
(1)如图,△ABC 中, AB =AC, ∠A =36°, 则∠B
= °;探究点二 等腰三角形性质的运用例1 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
求△ABC各角的度数.
思考:图中有哪些三角形是等腰三角形?图中有哪些角相等?灵活地应用等腰三角形的性质找相等的角,是解决该问题的突破点;再结合代数思想,应用列方程的方法,是在几何题中求解角或边的大小常用方法.反思归纳:当等腰三角形的边、角不确定时,应考虑什么问题?用到了什么数学思想?等腰三角形的边、角不确定时,应考虑是底边还是腰,是顶角还是底角.用到了分类讨论的数学思想.例2
探究点二 等腰三角形性质的运用三条边都相等的三角形是等边三角形. 问题 满足什么条件的三角形是等边三角形? 探究点三 等边三角形的性质 联系:等边三角形是特殊的等腰三角形;
区别:等边三角形有三条相等的边,而等腰三角形
只有两条. 请分别画出一个等腰三角形和等边三角形,结合
你画的图形说出它们有什么区别和联系? 思考 将等腰三角形的性质用于等边三角形,你能
得到什么结论?
从边的角度:两腰相等;
从角的角度:等边对等角;
从对称性的角度:轴对称图形、三线合一. 问题 等腰三角形有哪些特殊的性质呢? 细心观察,探索性质 结合等腰三角形的性质,你能填出等边三角形对应
的结论吗? 对“等边三角形的三个内角都相等,并且每一个角
都等于60°”这一结论进行证明.
证明:∵ △ABC 是等边三角形,
∴ BC =AC,BC =AB.
∴ ∠A =∠B,∠A =∠C .
∴ ∠A =∠B =∠C .
∵ ∠A +∠B +∠C =180°,
∴ ∠A =60°.
∴ ∠A =∠B =∠C =60°. 已知:△ABC 是等边三角形 求证:∠A =∠B =∠C
=60°. 符号语言:
∵ △ABC 是等边三角形,
∴ ∠A =∠B =∠C =60°.细心观察,探索性质 等边三角形的性质:
等边三角形的三个内角都相等,并且每一个角都等
于60°.1、等腰三角形的顶角是36度,则底角是_____________.
2、若等腰三角形的两边长分别是3m和6cm ,则其周长是____________.
3.下列命题中:(1)等腰三角形的两角相等;(2)等腰三角形的顶角平分线必平分底边;(3)等腰三角形一边上的中线也是这边上的高线;(4) 等腰三角形底边上的高线平分顶角.其中正确的有( )
A. (1)(3) B. (2)(4) C. (1)(2)(4) D. (2)(3)(4)
课堂练习4.如图,△ABC中,AB=AC,DE为BC上两点,AD=AE,
求证:BD=CE.5.如图,△ABC是等边三角形,BD、CE是中线,求∠CBD,∠BOE,∠BOC,∠EOD的度数。
(1)本节课学习了哪些内容?
(2)等腰三角形有哪些性质?等边三角形有哪些性质?
(3)结合本节课的学习,谈谈如何灵活利用等腰三角形和等边三角形性质.
课堂小结习题5.3 第1、2、3题课后作业
七年级
下册请同学们拿出一张长方形纸片,按照老师要求对折,然后用剪刀或小刀裁去阴影部分,再把裁剪后的直角三角形展开.得到的三角形有什么是什么三角形呢?情景导入1.从折剪的过程可知,△ABC是什么三角形呢?
2.在上述△ABC中,AB、AC、BC,∠B、∠C的名称是什么呢?
3.上面剪出的等腰△ABC是轴对称图形吗?如果是,其对称轴是什么(借助图中的线表示)?
(1)由折叠和对称可知,在△ABC中,∠B与∠C的大小关系如何;
(2)由折叠和对称又可知:∠BAD与∠DAC, BD与DC大小关系如何, AD与BC的位置关系是什么?1.掌握等腰三角形的性质,体会数学中的转化思想;
2.能运用等腰三角形的性质进行证明和计算.
学习目标 利用实验操作的方法,我们发现并概括出等腰三角
形的性质1和性质2.对于性质1,你能通过严格的逻辑
推理证明这个结论吗?
(1)你能根据结论画出图形,写出已知、求证吗?
(2)结合所画的图形,你认为证明两个底角相等的思
路是什么?
(3)如何在一个等腰三角形中构造出两个全等三角形
呢?从剪图、折纸的过程中你能获得什么启发? 探究点一 等腰三角形性质讲授新课 已知:如图,△ABC 中,AB =AC.求证:∠B =
∠C. 证明:作底边的中线AD.
∵ AB =AC,
BD =CD,
AD =AD,
∴ △ABD ≌△ACD(SSS).
∴ ∠B =∠C.证明等腰三角形的性质 你还有其他方法证明性质1吗?证明等腰三角形的性质 可以作底边的高线或顶角的角平分线. 性质2可以分解为三个命题,本节课证明“等腰三
角形的底边上的中线也是底边上的高和顶角平分线”. 已知:如图,△ABC 中,AB =AC,AD 是底边BC
的中线.求证:∠BAD =∠CAD,AD⊥BC.证明等腰三角形的性质 证明:∵ AD 是底边BC 的中线,
∴ BD =CD.
∵ AB =AC,
BD =CD,
AD =AD,
∴ △ABD ≌△ACD(SSS).证明等腰三角形的性质 已知:如图,△ABC 中,AB =AC,AD 是底边BC
的中线.求证:∠BAD =∠CAD,AD⊥BC. 证明:∴ ∠BAD =∠CAD,
∠ADB =∠ADC.
∵ ∠ADB +∠ADC =180°,
∴ ∠ADB =90°.
∴ AD⊥BC.探索并证明等腰三角形的性质 在等腰三角形性质的探索过程和证明过程中,“折
痕”“辅助线”发挥了非常重要的作用,由此,你能发
现等腰三角形具有什么特征?
等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴.课堂练习 练习1 填空:
(1)如图,△ABC 中, AB =AC, ∠A =36°, 则∠B
= °;探究点二 等腰三角形性质的运用例1 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
求△ABC各角的度数.
思考:图中有哪些三角形是等腰三角形?图中有哪些角相等?灵活地应用等腰三角形的性质找相等的角,是解决该问题的突破点;再结合代数思想,应用列方程的方法,是在几何题中求解角或边的大小常用方法.反思归纳:当等腰三角形的边、角不确定时,应考虑什么问题?用到了什么数学思想?等腰三角形的边、角不确定时,应考虑是底边还是腰,是顶角还是底角.用到了分类讨论的数学思想.例2
探究点二 等腰三角形性质的运用三条边都相等的三角形是等边三角形. 问题 满足什么条件的三角形是等边三角形? 探究点三 等边三角形的性质 联系:等边三角形是特殊的等腰三角形;
区别:等边三角形有三条相等的边,而等腰三角形
只有两条. 请分别画出一个等腰三角形和等边三角形,结合
你画的图形说出它们有什么区别和联系? 思考 将等腰三角形的性质用于等边三角形,你能
得到什么结论?
从边的角度:两腰相等;
从角的角度:等边对等角;
从对称性的角度:轴对称图形、三线合一. 问题 等腰三角形有哪些特殊的性质呢? 细心观察,探索性质 结合等腰三角形的性质,你能填出等边三角形对应
的结论吗? 对“等边三角形的三个内角都相等,并且每一个角
都等于60°”这一结论进行证明.
证明:∵ △ABC 是等边三角形,
∴ BC =AC,BC =AB.
∴ ∠A =∠B,∠A =∠C .
∴ ∠A =∠B =∠C .
∵ ∠A +∠B +∠C =180°,
∴ ∠A =60°.
∴ ∠A =∠B =∠C =60°. 已知:△ABC 是等边三角形 求证:∠A =∠B =∠C
=60°. 符号语言:
∵ △ABC 是等边三角形,
∴ ∠A =∠B =∠C =60°.细心观察,探索性质 等边三角形的性质:
等边三角形的三个内角都相等,并且每一个角都等
于60°.1、等腰三角形的顶角是36度,则底角是_____________.
2、若等腰三角形的两边长分别是3m和6cm ,则其周长是____________.
3.下列命题中:(1)等腰三角形的两角相等;(2)等腰三角形的顶角平分线必平分底边;(3)等腰三角形一边上的中线也是这边上的高线;(4) 等腰三角形底边上的高线平分顶角.其中正确的有( )
A. (1)(3) B. (2)(4) C. (1)(2)(4) D. (2)(3)(4)
课堂练习4.如图,△ABC中,AB=AC,DE为BC上两点,AD=AE,
求证:BD=CE.5.如图,△ABC是等边三角形,BD、CE是中线,求∠CBD,∠BOE,∠BOC,∠EOD的度数。
(1)本节课学习了哪些内容?
(2)等腰三角形有哪些性质?等边三角形有哪些性质?
(3)结合本节课的学习,谈谈如何灵活利用等腰三角形和等边三角形性质.
课堂小结习题5.3 第1、2、3题课后作业
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
