浙教版科学中考集训:6.1 简单机械(杠杆)(含解析)
文档属性
| 名称 | 浙教版科学中考集训:6.1 简单机械(杠杆)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2020-01-11 16:01:50 | ||
图片预览




文档简介
中考特训6 简单机械
6.1 杠杆
重难考点清单
杠杆力臂作图
杠杆最小力,力的动态变化
能否再次平衡
杠杆考虑重力时的解答计算
不均匀杠杆平衡问题
支点移动时的分析,如吊机
杠杆与浮力、压强、滑轮等结合分析
1、如图所示,质地均匀的圆柱体,在拉力F的作用下,由实线位置匀速转到虚线所示位置,整个过程中,拉力F始终作用于A点且与OA保持垂直(OA为圆柱体横截面的直径),圆柱体在转动过程中不打滑。则下列分析正确的是( ?A??)
A.拉力F逐渐变小
B.由于拉力F的力臂始终保持最长,拉力F始终保持最小值不变
C.拉力F逐渐变大
D.条件不足,无法判断
【解析】动力F的力臂L始终保持不变,阻力为圆柱体的重力G始终大小不变,由实线位置转到虚线位置时,重力的力臂逐渐减小,又因为FL=GL′,所以动力F逐渐变小。
注意:需要找出的等量关系。动力臂大小不变,重力的大小不变。根据杠杆平衡就可以找出力F大小与重力臂变化的关系。
2、如图所示,轻质杠杆的支点为 O ,在杠杆的 A 点始终作用竖直向上的力 F ,将重为 G 的物体匀速提升,则力 F 的大小( C );重力的力臂的大小 ( B );拉力的力臂的大小 ( B )
A、逐步变大巧玲珑 B、逐步变小 C、始终不变 D、先变小后变大,杠杆在水平位置上下最小
3、如图所示,两个等高的托盘秤甲、乙放在同一水平地面上,质量分布不均匀的木条AB重24N,A、B是木条两端,O、C是木条上的两个点,AO=BO,AC=OC.A端放在托盘秤甲上,B端放在托盘秤乙上,托盘秤甲的示数是6N.现移动托盘秤甲,让C点放在托盘秤甲上。此时托盘秤乙的示数是( C )
A.8N B.12N C.16N D.18N
4、如图所示,货物G重280N,动滑轮重20N,为使杠杆平衡,则竖直向上的力F的大小为(杠杆重、绳重、摩擦都忽略不计)( B )
A、100N B、200N C、300N D、400N
【解析】物体和动滑轮由2段绳子承担,∴杠杆A的力:FA=1/2(G+G动) =150N;
设杠杆的一个小格是L,根据杠杆平衡条件得,FA×OA=F×OB,
150N×4L=F×3L,∴F=200N; 故选B。
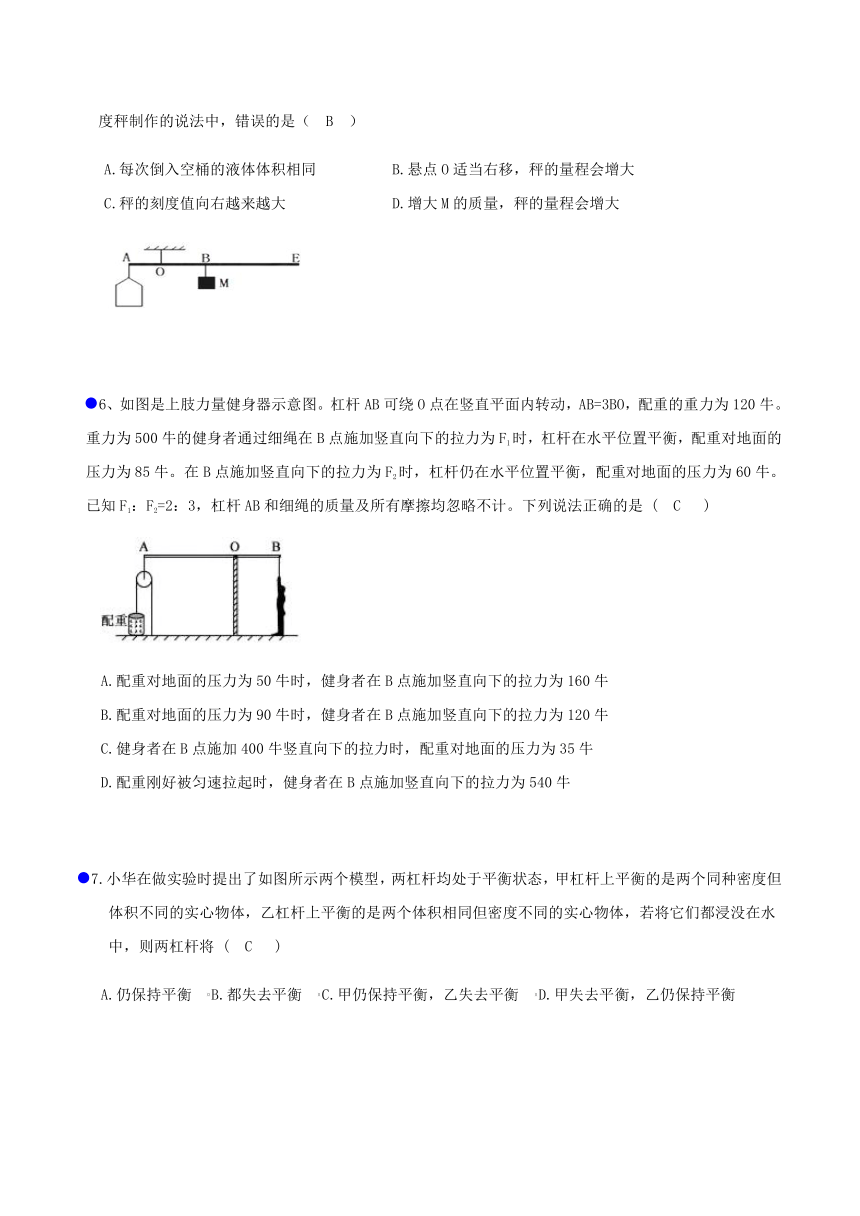
5.如图小明用一轻质杠杆自制简易密度秤的过程中,在A端的空桶内分别注入密度已知的不同液体,改变物体M悬挂点B的位置,当杠杆在水平位置平衡时,在M悬挂点处标出相应液体的密度值。下列关于密度秤制作的说法中,错误的是( B )
每次倒入空桶的液体体积相同?????B.悬点O适当右移,秤的量程会增大 C.秤的刻度值向右越来越大???????D.增大M的质量,秤的量程会增大
6、如图是上肢力量健身器示意图。杠杆AB可绕O点在竖直平面内转动,AB=3BO,配重的重力为120牛。重力为500牛的健身者通过细绳在B点施加竖直向下的拉力为F1时,杠杆在水平位置平衡,配重对地面的压力为85牛。在B点施加竖直向下的拉力为F2时,杠杆仍在水平位置平衡,配重对地面的压力为60牛。已知F1:F2=2:3,杠杆AB和细绳的质量及所有摩擦均忽略不计。下列说法正确的是 (?C? )
A.配重对地面的压力为50牛时,健身者在B点施加竖直向下的拉力为160牛 B.配重对地面的压力为90牛时,健身者在B点施加竖直向下的拉力为120牛 C.健身者在B点施加400牛竖直向下的拉力时,配重对地面的压力为35牛 D.配重刚好被匀速拉起时,健身者在B点施加竖直向下的拉力为540牛
7.小华在做实验时提出了如图所示两个模型,两杠杆均处于平衡状态,甲杠杆上平衡的是两个同种密度但体积不同的实心物体,乙杠杆上平衡的是两个体积相同但密度不同的实心物体,若将它们都浸没在水中,则两杠杆将 (?C? )
A.仍保持平衡?B.都失去平衡?C.甲仍保持平衡,乙失去平衡?D.甲失去平衡,乙仍保持平衡
8、密度均匀的直尺AB放在水平桌面上,尺子伸出桌面的部分OB是全尺长的三分之一,当B端挂5N的重物P时,直尺A端刚刚开始翘起,如图所示,则此直尺受到重力是( C )
A. 2.5N B. 5N C. 10N D. 无法确定
【解析】设直尺长为L。从图示可以看出:杠杆的支点为O,动力大小等于物重5N,动力臂为1/3L;阻力为直尺的重力G′,阻力的力臂为1/2L-1/3L=1/6L;
由杠杆平衡的条件得:G′L′=GL
G′×1/6L= 5N×1/3L G′=10N
注意:均匀规则物体的重心位于物体的几何中心。
9.如图所示用方向不变的力F,将杠杆从A位置匀速提升到B位置的过程中,F的大小变化情况是( A )
A. 保持不变 B.逐渐变小 C.逐渐变大 D.无法判定
10、如图所示,两完全相同的实心物体A,B通过细绳系于可绕O点转动的轻质杠杆MON的两端,其中物体A置于水平地面上,物体B悬于空中,两物体均保持静止,杠杆在水平位置保持平衡,已知两细绳均沿竖直方向,OM:ON=3:2,物体A,B都是高为10cm的长方体,其密度为0.9×103 kg/m3 ,取g=10N/kg,则物体A对水平地面的压强为( B )
A、0? B、300Pa? C、600Pa? D、900Pa
【解析】设长方体的底面积为S,则长方体的体积V=Sh,
由ρ=m/v和G=mg可得,长方体的重力:G=mg=ρVg=ρShg,
由杠杆的平衡条件可得:FM?OM=GB?ON,则:FM=GB=2/3G,
物体A对水平地面的压力:F=G﹣FM=G﹣2/3G=1/3G,
物体A对水平地面的压强:p=F/S=1/3G/S=1/3ρhg=1/3×0.9×103kg/m3×0.1m×10N/kg=300Pa。
故选B。
11、如图所示,在杠杆OA的B点悬挂一个重物G,A端用细绳吊在小圆环M的下,且细绳长AM等于圆弧环PMQ半径,此时杠杆恰处于水平状态,A点与圆弧环PMQ的圆心重合。当M环从P点逐渐沿顺时针滑到Q点的过程中,吊绳对A端的作用力大小将( D )
A.逐渐变大 B.逐渐变小
C.先变大后变小 D.先变小后变大
【解析】当滑环从P点逐渐滑到Q点的过程中,物体的重以及重力的力臂不变;拉力的力臂先变大、后变小(当MA垂直于OA时,拉力的力臂最大);根据F1×L1=F2×L2,可知拉力先变小后变大。
12、如图所示两杠杆处于平衡状态,甲中的是两个同种密度但体积不同的物体,乙上的是两个体积相同但密度不同的物体,如果把他们都浸没在水中,则杠杆如何变化(?C )
A、仍保持平衡
B、都失去平衡
C、甲仍保持平衡,乙失去平衡
D、甲失去平衡,乙仍保持平衡
【解析】甲杠杆:浸入水中之前:ρ物gV1×L1=ρ物gV2×L2所以V1×L1=V2×L2
浸入水中后左端力和力臂的乘积为:(ρ物gV1﹣ρ水gV1)×L1=(ρ物﹣ρ水)gV1×L1
浸入水中后右端力和力臂的乘积为:(ρ物gV2﹣ρ水gV2)×L2=(ρ物﹣ρ水)gV2×L2
所以浸入水中后,左右两端力和力臂的乘积相等,故杠杆仍然平衡。
乙杠杆:浸入水中之前:ρ铝gV×L1=ρ铁gV×L2
浸入水中后左端力和力臂的乘积为:(ρ铝gV﹣ρ水gV)×L1=ρ铝gV×L1﹣ρ铝gV×L1
浸入水中后左端力和力臂的乘积为:(ρ铁gV﹣ρ水gV)×L1=ρ铁gV×L2﹣ρ铁gV×L2
因为L1>L2,所以,左端力和力臂的乘积小于右端力和力臂的乘积,
故杠杆右端下沉,综上所述,选项C符合题意。故答案为:C
13.如图所示,将一轻质薄木板从中点支起,左右两侧各有一支蜡烛,长短不同,此时薄木板恰好在水平位置静止。同时点燃两支蜡烛,过一会儿,薄木板可能发生的情况是( A )
A. 长蜡烛燃烧较快,可能再次平衡 B.不可能再次平衡
C.燃烧速度相同,可能再次平衡 D.短蜡烛燃烧较快,可能再次平衡
14、如图所示,质量分布均匀的长方体砖,平放在水平地面上,第一次用竖直向上的力F1只作用于ab的中点,第二次用竖直向上的力F2作用于bc的中点,都使它们在竖直方向上慢慢向上移动h(h<ab<bc),则在上述过程中F1________F2(选填“大于”、“小于”或“等于”);F1所做的功F1________F2所做的功(选填“大于”、“小于”或“等于”);第一次克服重力所做的功________第二次克服重力所做的功(选镇“大于”、“小于”或“等于”)。
【答案】等于,等于,等于
【解析】F1 和 F2向上拉物体时,动力臂的长度均为阻力臂长度的2倍,则动力的大小也均为阻力大小的一半,即长方体砖重力大小的一半。F1 和 F2在竖直方向上均移动h,由W=FS得,F1 和 F2所做的功大小相等。在两次移动过程中,重心移动的高度也相等,重力大小不变。则两次克服重力所做的功也相等。
15.如图所示,两个完全相同的托盘秤甲和乙放在水平地面上,托盘秤的自重为9N.底面积为150cm2。术条AB质量分布不均匀(粗细忽略不计),A、B是木条两端,C、D是木条上的两个点,AD=BD,AC=DC。A端放在甲上,B端放在乙上,A、B下方各垫有一个大小和质量不计的小木块,甲的示数是6N,乙的示数是18N。则甲对地面的压强是____1000____Pa;若此时用细线系住A端,竖直向上拉细线,使A端缓慢上升,此过程中乙的示数_____不变___(选填“变大”“变小”或“不变”);若移动甲,让C点放在甲上,则乙的示数是____16____N。
16.如图所示,OAB是杠杆,OA与BA垂直,在OA的中点处挂一个G=10 N的重物,杠杆重力及摩擦均不计。若加在B点的动力F甲使OA在水平位置保持静止,如图甲所示,那么,该杠杆 __不一定__(选填“一定”或“不一定”)是省力杠杆;若动力F乙始终与OA垂直,将杠杆由水平位置匀速向上提升重物,如图乙所示,动力F乙的大小变化是__变小__(选填“变大”“变小”“先变大后变小”或“先变小后变大”);若动力F丙由竖直向上的方向沿逆时针缓慢地转到水平向左的方向,在此过程中OA始终保持水平静止,如图丙所示。请画出动力F丙随时间t的变化趋势。
17、如图所示,一轻质杠杆支在支架上,OA=20cm,G1为边长是5cm的正方体,G2重为20N。当OC=l0cm时,绳子的拉力为________N,此时G1对地面的压强为2×104Pa。现用一水平拉力,使G2以________cm/s的速度向右匀速运动,经过12.5s后,可使G1对地面的压力恰好为零。
【解析】根据杠杆平衡条件可得:FA*OA=G2*OC,所以FA=10N;
G1的底面积为:S1=2.5×10-3m2 ,
它对地面的压力为:F1=P1S1=50N,G1地面对的支持力与G1对地面的压力是一对作用力与反作用力,大小相等,所以F支=50N,G1的重力为:G1=F1+F支=60N,
G1对地面的压力恰好为零时,设G2的力臂为L2,根据杠杆平衡条件得:G1×OA=G2×L2 , L2=60cm,G2则向右移动d的距离s=60cm-10cm=50cm,其速度为:v=S/t=4cm/s。
18.如图所示,有一粗细均匀,重为40N,长为4m的长木板AB,置于支架上,支点为0,且AO=1m,长木板的右端B用绳子系住,绳子另一端固定在C处,当长木板AB水平时,绳与水平成30°的夹角,且绳子所能承受的最大拉力为60N.一个重为50N的体积不计的滑块M在F=10N的水平拉力作用下,从AO之间某处以V=1m/s的速度向B端匀速滑动,则:
①滑块匀速运动时所受的摩擦力的大小是___10_____N;
②当滑块匀速运动时拉力F做功的功率是____10____W.
③滑块在O点左侧_____0.8m___到右测_____1m___范围内滑动才能使AB保持水平.
19.如图所示,将长为1.2 米的轻质木棒平放在水平方形台面上,左右两端点分别为A、B,它们距台面边缘处的距离均为0.3米。在A端挂一个重为30牛的物体,在B端挂一个重为G的物体。
(1)若 G=30牛,台面收到木棒的压力为____60____牛。
(2)若 B 端挂物体后,木棒仍在水平台面上静止,则G的取值范围为_____10-90___牛
20.小明同学在“研究杠杆平衡条件”实验中:
(1) 将杠杆支点设在中间的目的是__避免杠杆自重对实验的影响__。
(2)实验时应先调节杠杆在__水平__位置平衡。目的是__方便读取力臂__,若出现图甲所示情况,应将杠杆的螺母向__左__(选填“左”或“右”)调。
(3)杠杆平衡后,小明在图乙所示的A位置挂上3个钩码,为了使杠杆在水平位置平衡,这时应在B位置挂上__4__个钩码。
(4)下表是该组某同学在实验中记录杠杆平衡的部分数据:
实验次数
F1(N)
l1(cm)
F2(N)
l2(cm)
1
2
5
△
10
2
3
10
2
15
3
2
30
3
☆
上表中空格处所缺的数据是:△=__1__,☆=__20__。
(5)分析上表中的实验数据可以得出的结论是__F1l1=F2l2(动力×动力臂=阻力×阻力臂)__。
21.如图所示重力不计的木棒AOB可绕支点O无摩擦转动,木棒AB长为3 m,均匀正方体甲的边长为10 cm,物体乙的质量为5.6 kg。当把甲、乙两物体用细绳分别挂在木棒的两个端点A、B上时,木棒在水平位置平衡,此时物体甲对地面的压强为3 000 Pa,支点O距A点1.6 m。求:
(1)物体乙受到的重力;
(2)物体甲受到的支持力;
(3)物体甲的密度。
【答案】 (1)物体乙受到的重力为56 N;(2)物体甲受到的支持力为30 N;(3)物体甲的密度为7.9×103 kg/m3。
22.如图所示装置,O为杠杆OA的支点,在离O点L0处挂着一个质量为M的物体。每单位长度杠杆的质量为m,当杠杆的长度为多少时,可以用最小的力F维持杠杆平衡。
【答案】根据图示可知,支点为O,阻力和阻力臂分别为物体的重力和对应的力臂L0,杠杆自身的重力和对应的力臂 LOA;动力为F和对应的力臂LOA;因此根据杠杆平衡的条件可得,
FLOA=MgLOA+ mLOAgLOA ?即 mgLOA2- FLOA+MGL0=0 LOA=
当 P2=2Mmg2L0时,力F最mg小,即LOA = 。
【解析】O点是杠杆的支点,质量为M的物体对杠杆的力为mg,力矩为mgL0;拉力F的力臂是OA,它的力矩是FLOA;每单位长度杠杆的质量为m,那么杠杆自身的重力为mLOAg,重力的力臂为 , 那么重力的力矩为:;根据杠杆的平衡条件列出平衡关系式,然后再利用数学知识求出F的最小值即可。
23、郝强同学对建筑工地上的长臂吊车(如图甲)有些疑惑:不吊物体它能平衡,吊重物也能平衡,重物沿臂移动仍能平衡!后来他通过设计“移动支点式杠杆”模型(如图乙)弄懂了类似问题:密度及粗细都均匀的直棒AB=1.8m,放在一个宽度为40cm的凳子上,当在棒的A端固定一个铅块(忽略大小)m铅=2kg时,棒刚好绕O1点有转动的趋势(AO1=30cm)。
(1)求棒的质量m棒;
(2)当在P处挂一重物时(PB=10cm),棒刚好绕O2点有转动的趋势。求重物质量m物及此时棒对O2点的压力F(g取10N/kg);
(3)当悬线带着重物缓慢向A端移动时,可以认为凳面上只有某点E(即新支点)对棒有支持力。回答:随着重物左移,E点将“左移”或“右移”还不“不动”?棒对E点的压力FE是“变大”或“变小”还是“不变”?(不必说明理由)
答案:如图:设棒的中心为O,则AO=90cm,O1O=60cm;
(1)以01为转轴,由杠杆平衡条件F1L1=F2L2得到平衡方程:
m铅g×AO1=m棒g×O1O, m铅g×30cm=m棒g×60cm,m棒=1/2 m铅=1/2×2kg=1kg;
(2)以02为转轴,平衡方程m铅g×AO2=m棒g×O2O+mg×02P,
即:m铅×AO2=m棒×O2O+m×02P,
2kg×70cm=1kg×20cm+m×100cm,m=1.2kg;
F=(m铅+m棒+m物)g=(2kg+1kg+1.2kg)×10N/kg=42N;
(3)随着重物左移,铅块、棒和物的总重心左移,凳面上某点E(即新支点)对棒支持力左移;竖直方向:压力等于铅块、棒、物三重力之和,压力FE不变
6.1 杠杆
重难考点清单
杠杆力臂作图
杠杆最小力,力的动态变化
能否再次平衡
杠杆考虑重力时的解答计算
不均匀杠杆平衡问题
支点移动时的分析,如吊机
杠杆与浮力、压强、滑轮等结合分析
1、如图所示,质地均匀的圆柱体,在拉力F的作用下,由实线位置匀速转到虚线所示位置,整个过程中,拉力F始终作用于A点且与OA保持垂直(OA为圆柱体横截面的直径),圆柱体在转动过程中不打滑。则下列分析正确的是( ?A??)
A.拉力F逐渐变小
B.由于拉力F的力臂始终保持最长,拉力F始终保持最小值不变
C.拉力F逐渐变大
D.条件不足,无法判断
【解析】动力F的力臂L始终保持不变,阻力为圆柱体的重力G始终大小不变,由实线位置转到虚线位置时,重力的力臂逐渐减小,又因为FL=GL′,所以动力F逐渐变小。
注意:需要找出的等量关系。动力臂大小不变,重力的大小不变。根据杠杆平衡就可以找出力F大小与重力臂变化的关系。
2、如图所示,轻质杠杆的支点为 O ,在杠杆的 A 点始终作用竖直向上的力 F ,将重为 G 的物体匀速提升,则力 F 的大小( C );重力的力臂的大小 ( B );拉力的力臂的大小 ( B )
A、逐步变大巧玲珑 B、逐步变小 C、始终不变 D、先变小后变大,杠杆在水平位置上下最小
3、如图所示,两个等高的托盘秤甲、乙放在同一水平地面上,质量分布不均匀的木条AB重24N,A、B是木条两端,O、C是木条上的两个点,AO=BO,AC=OC.A端放在托盘秤甲上,B端放在托盘秤乙上,托盘秤甲的示数是6N.现移动托盘秤甲,让C点放在托盘秤甲上。此时托盘秤乙的示数是( C )
A.8N B.12N C.16N D.18N
4、如图所示,货物G重280N,动滑轮重20N,为使杠杆平衡,则竖直向上的力F的大小为(杠杆重、绳重、摩擦都忽略不计)( B )
A、100N B、200N C、300N D、400N
【解析】物体和动滑轮由2段绳子承担,∴杠杆A的力:FA=1/2(G+G动) =150N;
设杠杆的一个小格是L,根据杠杆平衡条件得,FA×OA=F×OB,
150N×4L=F×3L,∴F=200N; 故选B。
5.如图小明用一轻质杠杆自制简易密度秤的过程中,在A端的空桶内分别注入密度已知的不同液体,改变物体M悬挂点B的位置,当杠杆在水平位置平衡时,在M悬挂点处标出相应液体的密度值。下列关于密度秤制作的说法中,错误的是( B )
每次倒入空桶的液体体积相同?????B.悬点O适当右移,秤的量程会增大 C.秤的刻度值向右越来越大???????D.增大M的质量,秤的量程会增大
6、如图是上肢力量健身器示意图。杠杆AB可绕O点在竖直平面内转动,AB=3BO,配重的重力为120牛。重力为500牛的健身者通过细绳在B点施加竖直向下的拉力为F1时,杠杆在水平位置平衡,配重对地面的压力为85牛。在B点施加竖直向下的拉力为F2时,杠杆仍在水平位置平衡,配重对地面的压力为60牛。已知F1:F2=2:3,杠杆AB和细绳的质量及所有摩擦均忽略不计。下列说法正确的是 (?C? )
A.配重对地面的压力为50牛时,健身者在B点施加竖直向下的拉力为160牛 B.配重对地面的压力为90牛时,健身者在B点施加竖直向下的拉力为120牛 C.健身者在B点施加400牛竖直向下的拉力时,配重对地面的压力为35牛 D.配重刚好被匀速拉起时,健身者在B点施加竖直向下的拉力为540牛
7.小华在做实验时提出了如图所示两个模型,两杠杆均处于平衡状态,甲杠杆上平衡的是两个同种密度但体积不同的实心物体,乙杠杆上平衡的是两个体积相同但密度不同的实心物体,若将它们都浸没在水中,则两杠杆将 (?C? )
A.仍保持平衡?B.都失去平衡?C.甲仍保持平衡,乙失去平衡?D.甲失去平衡,乙仍保持平衡
8、密度均匀的直尺AB放在水平桌面上,尺子伸出桌面的部分OB是全尺长的三分之一,当B端挂5N的重物P时,直尺A端刚刚开始翘起,如图所示,则此直尺受到重力是( C )
A. 2.5N B. 5N C. 10N D. 无法确定
【解析】设直尺长为L。从图示可以看出:杠杆的支点为O,动力大小等于物重5N,动力臂为1/3L;阻力为直尺的重力G′,阻力的力臂为1/2L-1/3L=1/6L;
由杠杆平衡的条件得:G′L′=GL
G′×1/6L= 5N×1/3L G′=10N
注意:均匀规则物体的重心位于物体的几何中心。
9.如图所示用方向不变的力F,将杠杆从A位置匀速提升到B位置的过程中,F的大小变化情况是( A )
A. 保持不变 B.逐渐变小 C.逐渐变大 D.无法判定
10、如图所示,两完全相同的实心物体A,B通过细绳系于可绕O点转动的轻质杠杆MON的两端,其中物体A置于水平地面上,物体B悬于空中,两物体均保持静止,杠杆在水平位置保持平衡,已知两细绳均沿竖直方向,OM:ON=3:2,物体A,B都是高为10cm的长方体,其密度为0.9×103 kg/m3 ,取g=10N/kg,则物体A对水平地面的压强为( B )
A、0? B、300Pa? C、600Pa? D、900Pa
【解析】设长方体的底面积为S,则长方体的体积V=Sh,
由ρ=m/v和G=mg可得,长方体的重力:G=mg=ρVg=ρShg,
由杠杆的平衡条件可得:FM?OM=GB?ON,则:FM=GB=2/3G,
物体A对水平地面的压力:F=G﹣FM=G﹣2/3G=1/3G,
物体A对水平地面的压强:p=F/S=1/3G/S=1/3ρhg=1/3×0.9×103kg/m3×0.1m×10N/kg=300Pa。
故选B。
11、如图所示,在杠杆OA的B点悬挂一个重物G,A端用细绳吊在小圆环M的下,且细绳长AM等于圆弧环PMQ半径,此时杠杆恰处于水平状态,A点与圆弧环PMQ的圆心重合。当M环从P点逐渐沿顺时针滑到Q点的过程中,吊绳对A端的作用力大小将( D )
A.逐渐变大 B.逐渐变小
C.先变大后变小 D.先变小后变大
【解析】当滑环从P点逐渐滑到Q点的过程中,物体的重以及重力的力臂不变;拉力的力臂先变大、后变小(当MA垂直于OA时,拉力的力臂最大);根据F1×L1=F2×L2,可知拉力先变小后变大。
12、如图所示两杠杆处于平衡状态,甲中的是两个同种密度但体积不同的物体,乙上的是两个体积相同但密度不同的物体,如果把他们都浸没在水中,则杠杆如何变化(?C )
A、仍保持平衡
B、都失去平衡
C、甲仍保持平衡,乙失去平衡
D、甲失去平衡,乙仍保持平衡
【解析】甲杠杆:浸入水中之前:ρ物gV1×L1=ρ物gV2×L2所以V1×L1=V2×L2
浸入水中后左端力和力臂的乘积为:(ρ物gV1﹣ρ水gV1)×L1=(ρ物﹣ρ水)gV1×L1
浸入水中后右端力和力臂的乘积为:(ρ物gV2﹣ρ水gV2)×L2=(ρ物﹣ρ水)gV2×L2
所以浸入水中后,左右两端力和力臂的乘积相等,故杠杆仍然平衡。
乙杠杆:浸入水中之前:ρ铝gV×L1=ρ铁gV×L2
浸入水中后左端力和力臂的乘积为:(ρ铝gV﹣ρ水gV)×L1=ρ铝gV×L1﹣ρ铝gV×L1
浸入水中后左端力和力臂的乘积为:(ρ铁gV﹣ρ水gV)×L1=ρ铁gV×L2﹣ρ铁gV×L2
因为L1>L2,所以,左端力和力臂的乘积小于右端力和力臂的乘积,
故杠杆右端下沉,综上所述,选项C符合题意。故答案为:C
13.如图所示,将一轻质薄木板从中点支起,左右两侧各有一支蜡烛,长短不同,此时薄木板恰好在水平位置静止。同时点燃两支蜡烛,过一会儿,薄木板可能发生的情况是( A )
A. 长蜡烛燃烧较快,可能再次平衡 B.不可能再次平衡
C.燃烧速度相同,可能再次平衡 D.短蜡烛燃烧较快,可能再次平衡
14、如图所示,质量分布均匀的长方体砖,平放在水平地面上,第一次用竖直向上的力F1只作用于ab的中点,第二次用竖直向上的力F2作用于bc的中点,都使它们在竖直方向上慢慢向上移动h(h<ab<bc),则在上述过程中F1________F2(选填“大于”、“小于”或“等于”);F1所做的功F1________F2所做的功(选填“大于”、“小于”或“等于”);第一次克服重力所做的功________第二次克服重力所做的功(选镇“大于”、“小于”或“等于”)。
【答案】等于,等于,等于
【解析】F1 和 F2向上拉物体时,动力臂的长度均为阻力臂长度的2倍,则动力的大小也均为阻力大小的一半,即长方体砖重力大小的一半。F1 和 F2在竖直方向上均移动h,由W=FS得,F1 和 F2所做的功大小相等。在两次移动过程中,重心移动的高度也相等,重力大小不变。则两次克服重力所做的功也相等。
15.如图所示,两个完全相同的托盘秤甲和乙放在水平地面上,托盘秤的自重为9N.底面积为150cm2。术条AB质量分布不均匀(粗细忽略不计),A、B是木条两端,C、D是木条上的两个点,AD=BD,AC=DC。A端放在甲上,B端放在乙上,A、B下方各垫有一个大小和质量不计的小木块,甲的示数是6N,乙的示数是18N。则甲对地面的压强是____1000____Pa;若此时用细线系住A端,竖直向上拉细线,使A端缓慢上升,此过程中乙的示数_____不变___(选填“变大”“变小”或“不变”);若移动甲,让C点放在甲上,则乙的示数是____16____N。
16.如图所示,OAB是杠杆,OA与BA垂直,在OA的中点处挂一个G=10 N的重物,杠杆重力及摩擦均不计。若加在B点的动力F甲使OA在水平位置保持静止,如图甲所示,那么,该杠杆 __不一定__(选填“一定”或“不一定”)是省力杠杆;若动力F乙始终与OA垂直,将杠杆由水平位置匀速向上提升重物,如图乙所示,动力F乙的大小变化是__变小__(选填“变大”“变小”“先变大后变小”或“先变小后变大”);若动力F丙由竖直向上的方向沿逆时针缓慢地转到水平向左的方向,在此过程中OA始终保持水平静止,如图丙所示。请画出动力F丙随时间t的变化趋势。
17、如图所示,一轻质杠杆支在支架上,OA=20cm,G1为边长是5cm的正方体,G2重为20N。当OC=l0cm时,绳子的拉力为________N,此时G1对地面的压强为2×104Pa。现用一水平拉力,使G2以________cm/s的速度向右匀速运动,经过12.5s后,可使G1对地面的压力恰好为零。
【解析】根据杠杆平衡条件可得:FA*OA=G2*OC,所以FA=10N;
G1的底面积为:S1=2.5×10-3m2 ,
它对地面的压力为:F1=P1S1=50N,G1地面对的支持力与G1对地面的压力是一对作用力与反作用力,大小相等,所以F支=50N,G1的重力为:G1=F1+F支=60N,
G1对地面的压力恰好为零时,设G2的力臂为L2,根据杠杆平衡条件得:G1×OA=G2×L2 , L2=60cm,G2则向右移动d的距离s=60cm-10cm=50cm,其速度为:v=S/t=4cm/s。
18.如图所示,有一粗细均匀,重为40N,长为4m的长木板AB,置于支架上,支点为0,且AO=1m,长木板的右端B用绳子系住,绳子另一端固定在C处,当长木板AB水平时,绳与水平成30°的夹角,且绳子所能承受的最大拉力为60N.一个重为50N的体积不计的滑块M在F=10N的水平拉力作用下,从AO之间某处以V=1m/s的速度向B端匀速滑动,则:
①滑块匀速运动时所受的摩擦力的大小是___10_____N;
②当滑块匀速运动时拉力F做功的功率是____10____W.
③滑块在O点左侧_____0.8m___到右测_____1m___范围内滑动才能使AB保持水平.
19.如图所示,将长为1.2 米的轻质木棒平放在水平方形台面上,左右两端点分别为A、B,它们距台面边缘处的距离均为0.3米。在A端挂一个重为30牛的物体,在B端挂一个重为G的物体。
(1)若 G=30牛,台面收到木棒的压力为____60____牛。
(2)若 B 端挂物体后,木棒仍在水平台面上静止,则G的取值范围为_____10-90___牛
20.小明同学在“研究杠杆平衡条件”实验中:
(1) 将杠杆支点设在中间的目的是__避免杠杆自重对实验的影响__。
(2)实验时应先调节杠杆在__水平__位置平衡。目的是__方便读取力臂__,若出现图甲所示情况,应将杠杆的螺母向__左__(选填“左”或“右”)调。
(3)杠杆平衡后,小明在图乙所示的A位置挂上3个钩码,为了使杠杆在水平位置平衡,这时应在B位置挂上__4__个钩码。
(4)下表是该组某同学在实验中记录杠杆平衡的部分数据:
实验次数
F1(N)
l1(cm)
F2(N)
l2(cm)
1
2
5
△
10
2
3
10
2
15
3
2
30
3
☆
上表中空格处所缺的数据是:△=__1__,☆=__20__。
(5)分析上表中的实验数据可以得出的结论是__F1l1=F2l2(动力×动力臂=阻力×阻力臂)__。
21.如图所示重力不计的木棒AOB可绕支点O无摩擦转动,木棒AB长为3 m,均匀正方体甲的边长为10 cm,物体乙的质量为5.6 kg。当把甲、乙两物体用细绳分别挂在木棒的两个端点A、B上时,木棒在水平位置平衡,此时物体甲对地面的压强为3 000 Pa,支点O距A点1.6 m。求:
(1)物体乙受到的重力;
(2)物体甲受到的支持力;
(3)物体甲的密度。
【答案】 (1)物体乙受到的重力为56 N;(2)物体甲受到的支持力为30 N;(3)物体甲的密度为7.9×103 kg/m3。
22.如图所示装置,O为杠杆OA的支点,在离O点L0处挂着一个质量为M的物体。每单位长度杠杆的质量为m,当杠杆的长度为多少时,可以用最小的力F维持杠杆平衡。
【答案】根据图示可知,支点为O,阻力和阻力臂分别为物体的重力和对应的力臂L0,杠杆自身的重力和对应的力臂 LOA;动力为F和对应的力臂LOA;因此根据杠杆平衡的条件可得,
FLOA=MgLOA+ mLOAgLOA ?即 mgLOA2- FLOA+MGL0=0 LOA=
当 P2=2Mmg2L0时,力F最mg小,即LOA = 。
【解析】O点是杠杆的支点,质量为M的物体对杠杆的力为mg,力矩为mgL0;拉力F的力臂是OA,它的力矩是FLOA;每单位长度杠杆的质量为m,那么杠杆自身的重力为mLOAg,重力的力臂为 , 那么重力的力矩为:;根据杠杆的平衡条件列出平衡关系式,然后再利用数学知识求出F的最小值即可。
23、郝强同学对建筑工地上的长臂吊车(如图甲)有些疑惑:不吊物体它能平衡,吊重物也能平衡,重物沿臂移动仍能平衡!后来他通过设计“移动支点式杠杆”模型(如图乙)弄懂了类似问题:密度及粗细都均匀的直棒AB=1.8m,放在一个宽度为40cm的凳子上,当在棒的A端固定一个铅块(忽略大小)m铅=2kg时,棒刚好绕O1点有转动的趋势(AO1=30cm)。
(1)求棒的质量m棒;
(2)当在P处挂一重物时(PB=10cm),棒刚好绕O2点有转动的趋势。求重物质量m物及此时棒对O2点的压力F(g取10N/kg);
(3)当悬线带着重物缓慢向A端移动时,可以认为凳面上只有某点E(即新支点)对棒有支持力。回答:随着重物左移,E点将“左移”或“右移”还不“不动”?棒对E点的压力FE是“变大”或“变小”还是“不变”?(不必说明理由)
答案:如图:设棒的中心为O,则AO=90cm,O1O=60cm;
(1)以01为转轴,由杠杆平衡条件F1L1=F2L2得到平衡方程:
m铅g×AO1=m棒g×O1O, m铅g×30cm=m棒g×60cm,m棒=1/2 m铅=1/2×2kg=1kg;
(2)以02为转轴,平衡方程m铅g×AO2=m棒g×O2O+mg×02P,
即:m铅×AO2=m棒×O2O+m×02P,
2kg×70cm=1kg×20cm+m×100cm,m=1.2kg;
F=(m铅+m棒+m物)g=(2kg+1kg+1.2kg)×10N/kg=42N;
(3)随着重物左移,铅块、棒和物的总重心左移,凳面上某点E(即新支点)对棒支持力左移;竖直方向:压力等于铅块、棒、物三重力之和,压力FE不变
