华师大版八年级上册数学第十二章整式的乘除与因式分解复习课件(共19张PPT)
文档属性
| 名称 | 华师大版八年级上册数学第十二章整式的乘除与因式分解复习课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 12:07:10 | ||
图片预览






文档简介
(共19张PPT)
第十二章 整式的乘除与因式分解
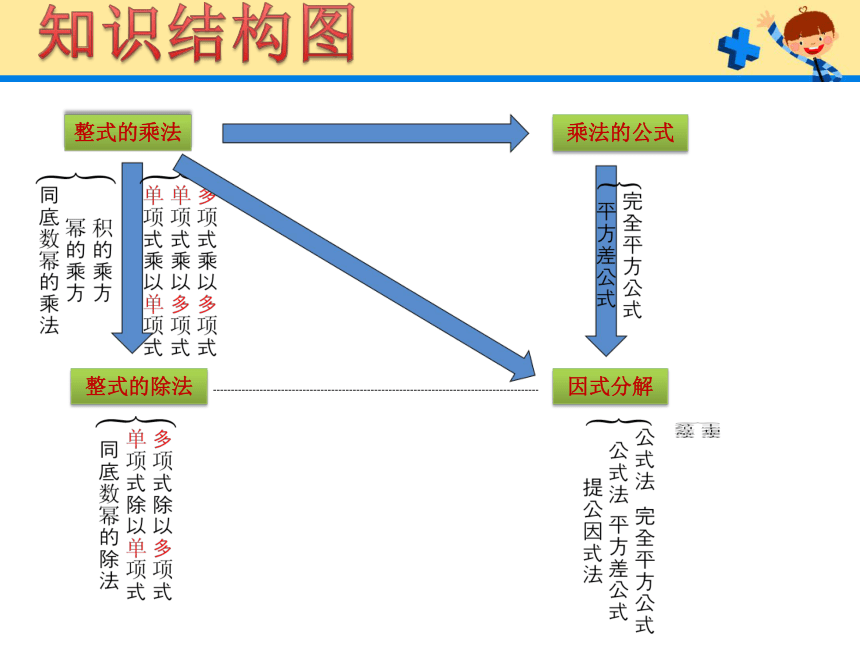
知识结构图
整式的乘法
整式的除法
乘法的公式
因式分解
?
?
?
?
?
知识清单
1、同底数幂乘法法则:am · an = am+n (m、n都是正整数)
同底数幂相乘,底数不变,指数相加
例1 计算:
(2) x2 · x5
(3) a·a6
(4) xm·x3m+1
(1) 23 × 24
解:
(1) 23 × 24 = 23+4 = 27
(2) x2 · x5 = x2+5 = x7
(3) a·a6 = a1+6 = a7
(4) xm·x3m+1 = xm+3m+1 = x4m+1
推广:am· an· ap = am+n+p (m、n、p都是正整数)
知识清单
2、幂的乘方法则:(am)n=amn (m,n都是正整数)
幂的乘方,底数不变,指数相乘
例2 计算:
解:
推广:[(am)n]p = amnp (m,n,p都是正整数)
逆用:
(1) (xn)5 (2)(24)3
(3) [(xy)3] 3m+1 (4) [(x+y)3 ] 2
(1) (xn)5= x5n
(2) (24)3 =24×3=212
(3) [ (xy)3 ]3m+1= (xy)3 ·(3m+1) =(xy)9m+3
(4) [(x+y)3 ] 2 =(x+y)3×2=(x+y)6
知识清单
3、积的乘方法则:(ab)n=anbn(n为正整数)
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
例3 计算:
解:
推广:(abc)n = anbncn(n为正整数)
逆用: anbncn = (abc)n
(1) (2a)3 ; (2) (-5b)3 ;
(3) (xy2)2 ; (4) (-2x3)4.
(1) (2a)3=23?a3 = 8a3;
(2) (-5b)3=(-5)3?b3=-125b3;
(3) (xy2)2=x2?(y2)2=x2y4;
(4) (-2x3)4=(-2)4?(x3)4=16x12.
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
知识清单
4、单项式与单项式相乘的法则:
例4 计算:(1) (-5a2b)(-3a); (2) (2x)3(-5xy2).
解:(1) (-5a2b)(-3a)
= [(-5)×(-3)](a2?a)b
= 15a3b
(2) (2x)3(-5xy2)
=8x3(-5xy2)
=[8×(-5)](x3?x)y2
=-40x4y2
(1) -5a3b2c·3a2b
(2)xy3 ·(-4x)2
(3) (-2xy2)3·(3x2y)2
练习:
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
知识清单
5、单项式与多项式相乘的法则:
例5 计算:
例6 先化简再求值:
答案:(1)
(2)
(3)
(4)
答案:化简得:
值为:
多项式乘以多项式,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
知识清单
6、多项式与多项式相乘的法则:
例7 计算:
练习:
答案:(1)
(3x+1)(x+2) (2) (x-8y)(x-y)
(3)(x+y)(x2-xy+y2)
3x2+7x+2
x2-9xy+8y2
x3+y3
(2)
(3)
(1)(2x+1)(x+3);
(2)(m+2n)(m-3n);
(3)(a+3b)(a-3b).
答案:(1)
(3)
(2)
两个数的和与这两个数的差的积,等于这两个数的平方差.即:
知识清单
7、平方差公式:
例8 用平方差公式计算:(x+2y)(x-2y)
练习:
(a+b)(a?b)=
a2?b2
解:原式= x2 - (2y)2
=x2 - 4y2
运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ;(2) (b+2a)(2a-b); (3) (-x+2y)(-x-2y); (4)2007×2013.
例9 化简:
(x4+y4 )
两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.即:
知识清单
8、完全平方公式:
练习:运用完全平方公式计算:
(1) (4m+n)2; (2) (y- )2 ; (3) 1022 ; (4) 992 .
(a+b)2=a2+2ab+b2, (a-b) 2 = a2-2ab +b2.
例9、运用完全平方公式计算:
(1)(4m+n)2
解: (1)(4m+n)2=
(4m)2
+2?(4m) ?n
+n2
=16m2
+8mn
+n2
(2)(x-2y)2
(2) (x-2y)2=
-2?x ?2y
+(2y)2
-4xy
+4y2
x2
=x2
?
知识清单
9、同底数幂的除法:
?
例10、计算:
?
?
?
?
?
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
知识清单
9、单项式除以单项式:
例11、计算:
?
?
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
10、多项式除以单项式:
?
?
例12、计算:
?
知识清单
11、因式分解:
(1)概念:把一个多项式化成几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
(2)因式分解的方法:提公因式法;公式法;分组分解法;十字相乘法
(3)如何找一个多项式各项的公因式:
系数:所有项的系数的最大公因数;
字母:应提取每一项都有的字母,且字母的指数取最低的;
系数与字母相乘
(4)用提公因式法分解因式的一般步骤:
第一步:找到该多项式的公因式;
第二步:将原式除以公因式,得到一个新多项式;
第三步:把它与公因式相乘。
知识清单
例13 将下列各式分解因式:
提高练习:
知识清单
12、公式法(平方差公式):
两个数的平方差等于这两个数的和与这两个数的差的积.
例14 将下列各式因式分解:
(1) – 4x2 + y2 (2) x4 – 1
解:(1)原式= y2 – 4x2 = (y+2x)(y–2x)
或 原式= – ( 4x2 – y2 ) = – (2x+y)(2x–y)
(2)原式= (x2)2 – 12 = (x2+1)(x2–1)
= (x2+1)(x+1)(x–1)
练习:将下列各式分解因式
(1)x2 – x6 (2)6x3 – 54xy2
知识清单
13、公式法(完全平方公式):
例14 将下列各式因式分解:
(1)16x2+24x+9(2)–4x2+4xy-y2
(3)4x2–8xy+4y2
两个数的平方和加上(或减去)这两个数的积的两倍,等于这两个数的和(或差)的平方。
知识清单
14、分组分解法
例:将下列各式因式分解:
(1) 4x2-4xy-a2+y2
(2)9m2-6m+2n-n2
知识清单
15:十字相乘法分解因式
例将下列各式因式分解:
(1)m?+4m-12
(2)
作业:练习册31-32页
第十二章 整式的乘除与因式分解
知识结构图
整式的乘法
整式的除法
乘法的公式
因式分解
?
?
?
?
?
知识清单
1、同底数幂乘法法则:am · an = am+n (m、n都是正整数)
同底数幂相乘,底数不变,指数相加
例1 计算:
(2) x2 · x5
(3) a·a6
(4) xm·x3m+1
(1) 23 × 24
解:
(1) 23 × 24 = 23+4 = 27
(2) x2 · x5 = x2+5 = x7
(3) a·a6 = a1+6 = a7
(4) xm·x3m+1 = xm+3m+1 = x4m+1
推广:am· an· ap = am+n+p (m、n、p都是正整数)
知识清单
2、幂的乘方法则:(am)n=amn (m,n都是正整数)
幂的乘方,底数不变,指数相乘
例2 计算:
解:
推广:[(am)n]p = amnp (m,n,p都是正整数)
逆用:
(1) (xn)5 (2)(24)3
(3) [(xy)3] 3m+1 (4) [(x+y)3 ] 2
(1) (xn)5= x5n
(2) (24)3 =24×3=212
(3) [ (xy)3 ]3m+1= (xy)3 ·(3m+1) =(xy)9m+3
(4) [(x+y)3 ] 2 =(x+y)3×2=(x+y)6
知识清单
3、积的乘方法则:(ab)n=anbn(n为正整数)
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
例3 计算:
解:
推广:(abc)n = anbncn(n为正整数)
逆用: anbncn = (abc)n
(1) (2a)3 ; (2) (-5b)3 ;
(3) (xy2)2 ; (4) (-2x3)4.
(1) (2a)3=23?a3 = 8a3;
(2) (-5b)3=(-5)3?b3=-125b3;
(3) (xy2)2=x2?(y2)2=x2y4;
(4) (-2x3)4=(-2)4?(x3)4=16x12.
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
知识清单
4、单项式与单项式相乘的法则:
例4 计算:(1) (-5a2b)(-3a); (2) (2x)3(-5xy2).
解:(1) (-5a2b)(-3a)
= [(-5)×(-3)](a2?a)b
= 15a3b
(2) (2x)3(-5xy2)
=8x3(-5xy2)
=[8×(-5)](x3?x)y2
=-40x4y2
(1) -5a3b2c·3a2b
(2)xy3 ·(-4x)2
(3) (-2xy2)3·(3x2y)2
练习:
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
知识清单
5、单项式与多项式相乘的法则:
例5 计算:
例6 先化简再求值:
答案:(1)
(2)
(3)
(4)
答案:化简得:
值为:
多项式乘以多项式,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
知识清单
6、多项式与多项式相乘的法则:
例7 计算:
练习:
答案:(1)
(3x+1)(x+2) (2) (x-8y)(x-y)
(3)(x+y)(x2-xy+y2)
3x2+7x+2
x2-9xy+8y2
x3+y3
(2)
(3)
(1)(2x+1)(x+3);
(2)(m+2n)(m-3n);
(3)(a+3b)(a-3b).
答案:(1)
(3)
(2)
两个数的和与这两个数的差的积,等于这两个数的平方差.即:
知识清单
7、平方差公式:
例8 用平方差公式计算:(x+2y)(x-2y)
练习:
(a+b)(a?b)=
a2?b2
解:原式= x2 - (2y)2
=x2 - 4y2
运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ;(2) (b+2a)(2a-b); (3) (-x+2y)(-x-2y); (4)2007×2013.
例9 化简:
(x4+y4 )
两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.即:
知识清单
8、完全平方公式:
练习:运用完全平方公式计算:
(1) (4m+n)2; (2) (y- )2 ; (3) 1022 ; (4) 992 .
(a+b)2=a2+2ab+b2, (a-b) 2 = a2-2ab +b2.
例9、运用完全平方公式计算:
(1)(4m+n)2
解: (1)(4m+n)2=
(4m)2
+2?(4m) ?n
+n2
=16m2
+8mn
+n2
(2)(x-2y)2
(2) (x-2y)2=
-2?x ?2y
+(2y)2
-4xy
+4y2
x2
=x2
?
知识清单
9、同底数幂的除法:
?
例10、计算:
?
?
?
?
?
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
知识清单
9、单项式除以单项式:
例11、计算:
?
?
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
10、多项式除以单项式:
?
?
例12、计算:
?
知识清单
11、因式分解:
(1)概念:把一个多项式化成几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
(2)因式分解的方法:提公因式法;公式法;分组分解法;十字相乘法
(3)如何找一个多项式各项的公因式:
系数:所有项的系数的最大公因数;
字母:应提取每一项都有的字母,且字母的指数取最低的;
系数与字母相乘
(4)用提公因式法分解因式的一般步骤:
第一步:找到该多项式的公因式;
第二步:将原式除以公因式,得到一个新多项式;
第三步:把它与公因式相乘。
知识清单
例13 将下列各式分解因式:
提高练习:
知识清单
12、公式法(平方差公式):
两个数的平方差等于这两个数的和与这两个数的差的积.
例14 将下列各式因式分解:
(1) – 4x2 + y2 (2) x4 – 1
解:(1)原式= y2 – 4x2 = (y+2x)(y–2x)
或 原式= – ( 4x2 – y2 ) = – (2x+y)(2x–y)
(2)原式= (x2)2 – 12 = (x2+1)(x2–1)
= (x2+1)(x+1)(x–1)
练习:将下列各式分解因式
(1)x2 – x6 (2)6x3 – 54xy2
知识清单
13、公式法(完全平方公式):
例14 将下列各式因式分解:
(1)16x2+24x+9(2)–4x2+4xy-y2
(3)4x2–8xy+4y2
两个数的平方和加上(或减去)这两个数的积的两倍,等于这两个数的和(或差)的平方。
知识清单
14、分组分解法
例:将下列各式因式分解:
(1) 4x2-4xy-a2+y2
(2)9m2-6m+2n-n2
知识清单
15:十字相乘法分解因式
例将下列各式因式分解:
(1)m?+4m-12
(2)
作业:练习册31-32页
