人教版2019-2020学年七年级数学下册 5.3.1 第2课时 平行线的性质与判定的综合应用课件(15张PPT)
文档属性
| 名称 | 人教版2019-2020学年七年级数学下册 5.3.1 第2课时 平行线的性质与判定的综合应用课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 211.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第 五 章 相交线与平行线
5.3平行线的性质
5.3.1 第2课时 平行线的性质与判定的综合应用
学习目标
1.进一步熟悉平行线的判定方法和性质;
2.运用平行线的性质和判定进行简单的
推理和计算;(重点、难点)
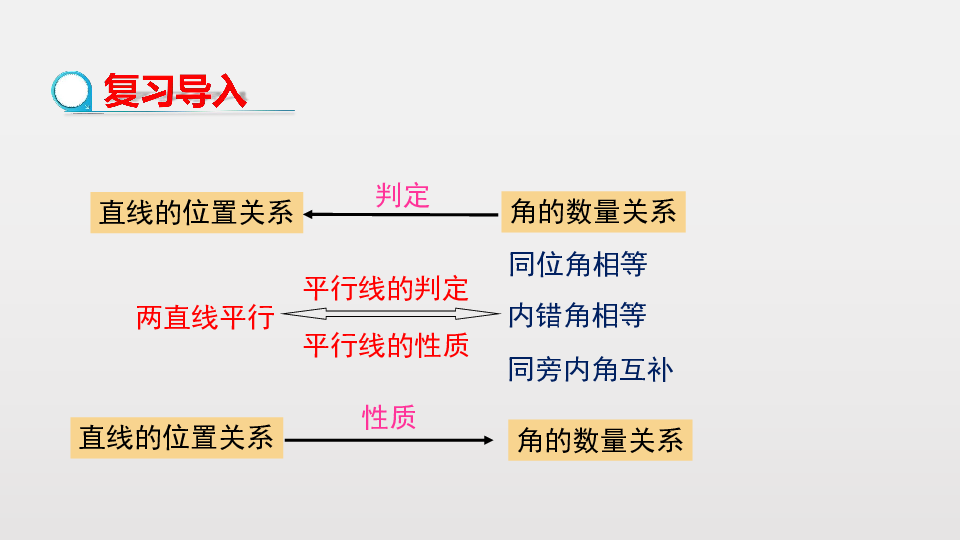
复习导入
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
直线的位置关系
角的数量关系
性质
角的数量关系
直线的位置关系
判定
知识讲解
例1 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=45°,∠B = 45°,∠AED=70°.
(1)DE和BC平行吗?为什么?
解:(1) DE∥BC.理由如下:
∵ ∠ADE=45°,∠B = 45°,
∴ ∠ADE=∠B,
∴ DE∥BC .
(同位角相等,两直线平行 ).
C
A
B
D
E
例1 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=45°,∠B = 45°,∠AED=70°.
(2)∠C是多少度?为什么?
C
A
B
D
E
解:∠C =70°.理由如下:
由(1)得DE∥BC,
∴ ∠C=∠AED .
(两直线平行,同位角相等)
又∵∠AED=70°,
∴ ∠C=∠AED =70°.
例2 如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
B
D
C
E
A
解:过点E 作EF//AB,
∴∠B=∠BEF.
∵AB//CD,
∴EF//CD,
∴∠D =∠DEF,
∴∠B+∠D=∠BEF+∠DEF =∠DEB,
即∠B+∠D=∠DEB.
F
变式1:如图,AB∥CD,则 :
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时: ∠A+∠E+∠C= 360°
当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°
当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
A
B
C
D
E1
E2
E3
…
A
B
C
D
E1
E2
En
当有n个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C = 180°
(n+1)
若有n个拐点,你能找到规律吗?
变式2:如图,若AB∥CD, 则:
A
B
C
D
E
当左边有两个角,右边有一个角时: ∠A+∠C= ∠E
当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当左边有三个角,右边有两个角时:∠A+∠ F1 +∠C = ∠ E1 +∠ E2
C
A
B
D
E1
F1
E2
Em
F2
Fn
∠A+∠F1 + ∠ F2 +…+ ∠Fn= ∠E1 +∠E2 +…+ ∠Em+ ∠D
当左边有n个角,右边有m个角时:
若左边有n个角,右边有m个角;你能找到规律吗?
随堂训练
1.直线a,b与直线c相交,给出下列条件:
①∠1= ∠2; ②∠3= ∠6;
③∠4+∠7=180o; ④∠3+ ∠5=180°,
其中能判断a//b的是( )
A. ①②③④
B .①③④
C. ①③
D. ④
1
2
3
4
5
6
7
8
c
a
b
B
3.如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )
A.80° B.85°
C.95° D.100°
B
4.如图,∠B=∠C,∠A=∠D,下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND,其中正确的结论有( )
A.①②④ B.②③④
C.③④ D.①②③④
A
5.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
解:∵∠1=∠2(已知),
∴AB∥EF
(内错角相等,两直线平行).
∵AB⊥BF,CD⊥BF,
∴AB∥CD
∴EF∥CD
∴ ∠3= ∠E
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,同位角相等).
6.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD
的度数.
解:∵EF∥AD(已知),
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DG∥AB.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
D
A
G
C
B
E
F
1
3
2
再见
第 五 章 相交线与平行线
5.3平行线的性质
5.3.1 第2课时 平行线的性质与判定的综合应用
学习目标
1.进一步熟悉平行线的判定方法和性质;
2.运用平行线的性质和判定进行简单的
推理和计算;(重点、难点)
复习导入
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
直线的位置关系
角的数量关系
性质
角的数量关系
直线的位置关系
判定
知识讲解
例1 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=45°,∠B = 45°,∠AED=70°.
(1)DE和BC平行吗?为什么?
解:(1) DE∥BC.理由如下:
∵ ∠ADE=45°,∠B = 45°,
∴ ∠ADE=∠B,
∴ DE∥BC .
(同位角相等,两直线平行 ).
C
A
B
D
E
例1 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=45°,∠B = 45°,∠AED=70°.
(2)∠C是多少度?为什么?
C
A
B
D
E
解:∠C =70°.理由如下:
由(1)得DE∥BC,
∴ ∠C=∠AED .
(两直线平行,同位角相等)
又∵∠AED=70°,
∴ ∠C=∠AED =70°.
例2 如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
B
D
C
E
A
解:过点E 作EF//AB,
∴∠B=∠BEF.
∵AB//CD,
∴EF//CD,
∴∠D =∠DEF,
∴∠B+∠D=∠BEF+∠DEF =∠DEB,
即∠B+∠D=∠DEB.
F
变式1:如图,AB∥CD,则 :
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时: ∠A+∠E+∠C= 360°
当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°
当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
A
B
C
D
E1
E2
E3
…
A
B
C
D
E1
E2
En
当有n个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C = 180°
(n+1)
若有n个拐点,你能找到规律吗?
变式2:如图,若AB∥CD, 则:
A
B
C
D
E
当左边有两个角,右边有一个角时: ∠A+∠C= ∠E
当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当左边有三个角,右边有两个角时:∠A+∠ F1 +∠C = ∠ E1 +∠ E2
C
A
B
D
E1
F1
E2
Em
F2
Fn
∠A+∠F1 + ∠ F2 +…+ ∠Fn= ∠E1 +∠E2 +…+ ∠Em+ ∠D
当左边有n个角,右边有m个角时:
若左边有n个角,右边有m个角;你能找到规律吗?
随堂训练
1.直线a,b与直线c相交,给出下列条件:
①∠1= ∠2; ②∠3= ∠6;
③∠4+∠7=180o; ④∠3+ ∠5=180°,
其中能判断a//b的是( )
A. ①②③④
B .①③④
C. ①③
D. ④
1
2
3
4
5
6
7
8
c
a
b
B
3.如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )
A.80° B.85°
C.95° D.100°
B
4.如图,∠B=∠C,∠A=∠D,下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND,其中正确的结论有( )
A.①②④ B.②③④
C.③④ D.①②③④
A
5.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
解:∵∠1=∠2(已知),
∴AB∥EF
(内错角相等,两直线平行).
∵AB⊥BF,CD⊥BF,
∴AB∥CD
∴EF∥CD
∴ ∠3= ∠E
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,同位角相等).
6.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD
的度数.
解:∵EF∥AD(已知),
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DG∥AB.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
D
A
G
C
B
E
F
1
3
2
再见
