五年级数学下册课件- ★ 探索图形 -人教新课标 (共15张PPT)
文档属性
| 名称 | 五年级数学下册课件- ★ 探索图形 -人教新课标 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1006.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
探索图形
人教版小学数学五年级(下)
数字接龙
1 12 123 1234
12=1×1=1 22=2×2=4 32=3×3=9
13=1×1×1=1 23=2×2×2=8 33=3×3×3=27
1cm
1cm
1cm
1cm
1cm
1cm
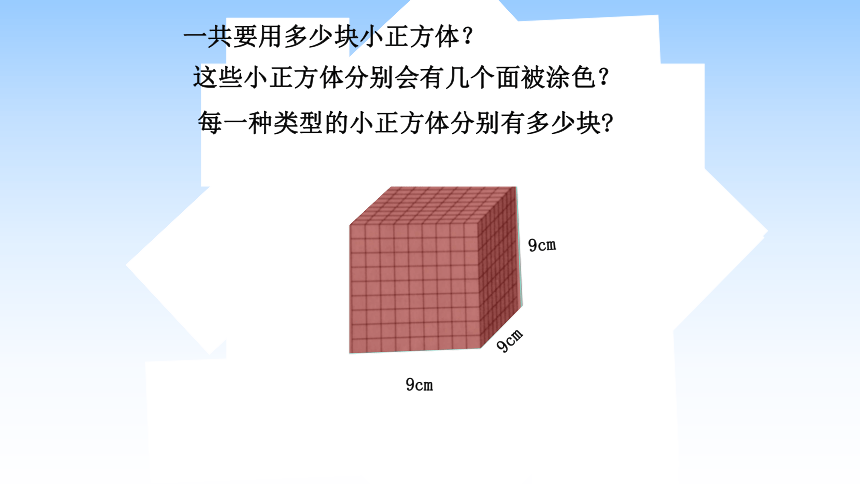
9cm
9cm
9cm
一共要用多少块小正方体?
这些小正方体分别会有几个面被涂色?
每一种类型的小正方体分别有多少块?
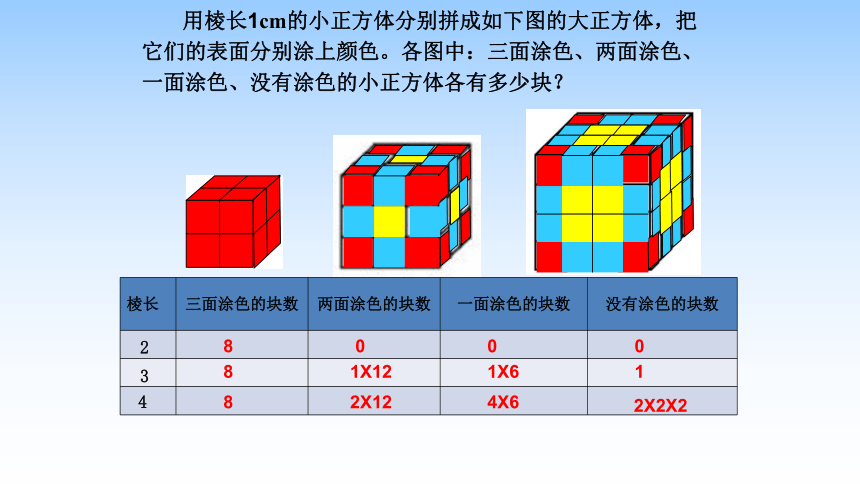
用棱长1cm的小正方体分别拼成如下图的大正方体,把它们的表面分别涂上颜色。各图中:三面涂色、两面涂色、一面涂色、没有涂色的小正方体各有多少块?
棱长 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
?
?
2
3
4
8
0
0
0
用棱长1cm的小正方体分别拼成如下图的大正方体,把它们的表面分别涂上颜色。各图中:三面涂色、两面涂色、一面涂色、没有涂色的小正方体各有多少块?
棱长 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
?
?
4X6
2X2X2
2
3
4
8
8
8
0
0
0
1X12
1X6
1
2X12
按这样的规律摆下去,棱长为5的图中:三面涂色、两面涂色、一面涂色、没有涂色的小正方体各有多少块?
棱长 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
?
?
?
22x6
23
8
3X12
32x6
8
4X12
42x6
2
3
4
5
6
8
8
8
0
0
0
1X12
1X6
1
2X12
33
43
三面涂色的小正方体都在大正方体的 的位置。因为正方体有 ,所以不论棱长是几,三面涂色的小正方体的个数都是 个。
8个顶点
顶点
8
规律1:
在 位置的正方体露出2个面,两面涂色的块数与 有关,即 。
每条棱上除去两端
棱
(n-2)×12
规律2:
在 位置的正方体露出1个面,一面涂色的块数与 有关,即 。
每个面除去四周一圈
面
(n-2)×(n-2)×6
规律3:
没有涂色的小正方体在每个大正方体的 位置,且又组成了 。
除去表面一层的
新正方体
一个棱长为( n-2 )的
规律4:
个数是(n-2)3个。
填表:
棱长 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
7
8
9
8
8
8
60
125
216
84
72
150
216
343
294
如果摆成下面的几何体,你会数吗?
4
10
20
作业:
谢 谢!
探索图形
人教版小学数学五年级(下)
数字接龙
1 12 123 1234
12=1×1=1 22=2×2=4 32=3×3=9
13=1×1×1=1 23=2×2×2=8 33=3×3×3=27
1cm
1cm
1cm
1cm
1cm
1cm
9cm
9cm
9cm
一共要用多少块小正方体?
这些小正方体分别会有几个面被涂色?
每一种类型的小正方体分别有多少块?
用棱长1cm的小正方体分别拼成如下图的大正方体,把它们的表面分别涂上颜色。各图中:三面涂色、两面涂色、一面涂色、没有涂色的小正方体各有多少块?
棱长 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
?
?
2
3
4
8
0
0
0
用棱长1cm的小正方体分别拼成如下图的大正方体,把它们的表面分别涂上颜色。各图中:三面涂色、两面涂色、一面涂色、没有涂色的小正方体各有多少块?
棱长 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
?
?
4X6
2X2X2
2
3
4
8
8
8
0
0
0
1X12
1X6
1
2X12
按这样的规律摆下去,棱长为5的图中:三面涂色、两面涂色、一面涂色、没有涂色的小正方体各有多少块?
棱长 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
?
?
?
22x6
23
8
3X12
32x6
8
4X12
42x6
2
3
4
5
6
8
8
8
0
0
0
1X12
1X6
1
2X12
33
43
三面涂色的小正方体都在大正方体的 的位置。因为正方体有 ,所以不论棱长是几,三面涂色的小正方体的个数都是 个。
8个顶点
顶点
8
规律1:
在 位置的正方体露出2个面,两面涂色的块数与 有关,即 。
每条棱上除去两端
棱
(n-2)×12
规律2:
在 位置的正方体露出1个面,一面涂色的块数与 有关,即 。
每个面除去四周一圈
面
(n-2)×(n-2)×6
规律3:
没有涂色的小正方体在每个大正方体的 位置,且又组成了 。
除去表面一层的
新正方体
一个棱长为( n-2 )的
规律4:
个数是(n-2)3个。
填表:
棱长 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
7
8
9
8
8
8
60
125
216
84
72
150
216
343
294
如果摆成下面的几何体,你会数吗?
4
10
20
作业:
谢 谢!
