鲁教版(五四制)九年级数学上册2.1锐角三角函数 专项练习 (含答案)
文档属性
| 名称 | 鲁教版(五四制)九年级数学上册2.1锐角三角函数 专项练习 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 512.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 00:00:00 | ||
图片预览




文档简介
锐角三角函数 专项练习
第一部分 知识梳理
一、基本知识
(一)锐角三角函数的定义
如图:
注意:三角函数是一个比值,只与角的大小有关,与所在的三角形,边的长短无关。
(二)、特殊角的三角函数值:
α 0° 30° 45° 60° 90°
sinα
cosα
tanα 不存在
结合图形进行求值:
1、含30°的直角三角形三边之比为:1: :2
2、含45°的直角三角形三边之比为:1:1 :
(三)、角度变化与锐角三角函数的关系?
当锐角α在00---900之间变化时,正弦(切)值随着角度的增大而增大;余弦值随着角度的增大而减少。
(四)、同角三角函数之间有哪些关系式?
1、平方关系:sin2A+cos2A=1;2、商的关系:
(五)、互为余角的三角函数关系
1、一个锐角的正弦等于它余角的余弦,一个锐角的余弦等于它余角的正弦
即:sin(900-A)=cosA;cos(900-A)=sinA;名变则角变,角变同时名也变;名变是指由正弦变成余弦或由余弦变正弦,角变成它的余角。
2、互余角的正切互为倒数:tanA.tan(90°-A)=1
第二部分 中考链接
一、三角函数定义
1.(2018日照)如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于( )A. B. C.2 D.
2.(2018?孝感)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于( )
A. B. C. D.
1题图 2题图 3题图 4题图 5题图
3.(2018?柳州)如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB==( )
A. B. C. D.
4.(2018?贵阳)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )A. B.1 C. D.
5.如图,已知点E是矩形ABCD的对角线AC上一动点,正方形EFGH的顶点G、H都在边AD上,若AB=3,BC=4,则tan∠AFE的值( ???)A.?等于?? B.等于??? C.等于?? D.随点E位置的变化而变化
6.(2018?枣庄)如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )A. B. C. D.
6题图 7题图 8题图 10题图 11题图
7. (2018潍坊)如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:
(1)作线段AB,分别以AB为圆心,以AB长为半径作弧,两弧的交点为C;
(2)以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
(3)连接BD,BC, 下列说法不正确的是( )
A.∠CBD=30 ° B. C. 点C是△ABD的外心 D. sin2A+cos2D=1
8.(2019·湖北宜昌)如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为( )A. B. C. D.
9.(2018?滨州)在△ABC中,∠C=90°,若tanA=,则sinB= .
10、(2018?德州)如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正弦值是 .
11.(2018?泰安)如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A'处,若EA'的延长线恰好过点C,则sin∠ABE的值为 .
12、(2018?眉山)如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD= .
12题图 13题图 15题图
13、(2018?广州)如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC= .
14.(2019?淄博)如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC边上的点D(不与点A,C重合)处,折痕是EF.
如图1,当CD=AC时,tanα1=; 如图2,当CD=AC时,tanα2=;
如图3,当CD=AC时,tanα3=; ……
依此类推,当CD=AC(n为正整数)时,tanαn= .
15.(2019·浙江舟山)如图,在△ABC中,若∠A=45°,AC2–BC2AB2,则tanC=__________.
二、特殊角的三角函数值
1、(2018日照)计算:()﹣1+tan30°?sin60°=( )A.﹣ B.2 C. D.
2.(2018?大庆)2cos60°=( )A.1 B. C. D.
3.(2018?天津)cos30°的值等于( )A. B. C.1 D.
4.(2019?天津)2sin60°的值等于( ) A.1 B. C. D.2
5.(2019?湖南怀化)已知∠α为锐角,且sinα=,则∠α=( )A.30°B.45°C.60°D.90°
6.【2019天津市滨海新区】的值等于( )A. B. C. D.
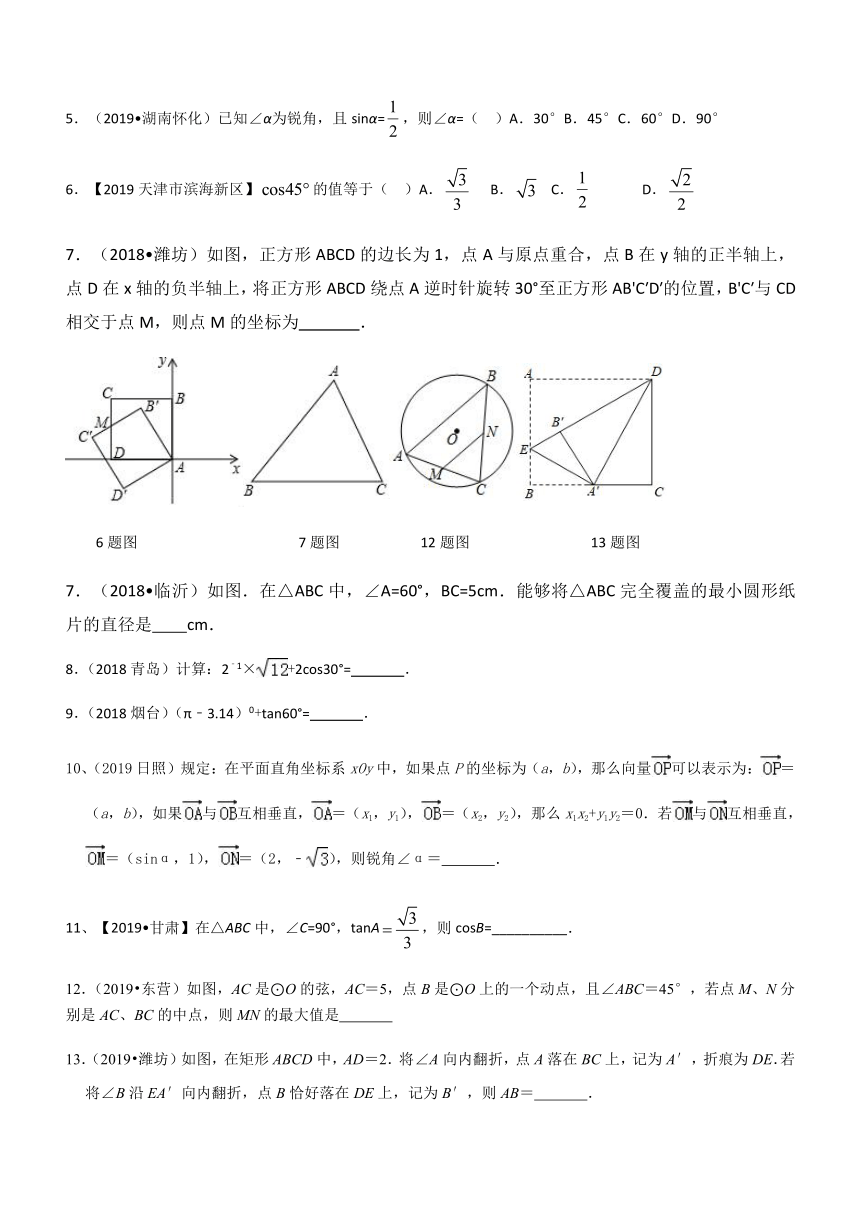
7.(2018?潍坊)如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为 .
6题图 7题图 12题图 13题图
7.(2018?临沂)如图.在△ABC中,∠A=60°,BC=5cm.能够将△ABC完全覆盖的最小圆形纸片的直径是 cm.
8.(2018青岛)计算:2﹣1×+2cos30°= .
9.(2018烟台)(π﹣3.14)0+tan60°= .
10、(2019日照)规定:在平面直角坐标系xOy中,如果点P的坐标为(a,b),那么向量可以表示为:=(a,b),如果与互相垂直,=(x1,y1),=(x2,y2),那么x1x2+y1y2=0.若与互相垂直,=(sinα,1),=(2,﹣),则锐角∠α= .
11、【2019?甘肃】在△ABC中,∠C=90°,tanA,则cosB=__________.
12.(2019?东营)如图,AC是⊙O的弦,AC=5,点B是⊙O上的一个动点,且∠ABC=45°,若点M、N分别是AC、BC的中点,则MN的最大值是
13.(2019?潍坊)如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为A′,折痕为DE.若将∠B沿EA′向内翻折,点B恰好落在DE上,记为B′,则AB= .
14.(2019?湖北荆门)计算+|sin30°﹣π0|+=__________.
15.(2019?湖北随州)计算:(π–2019)0–2cos60°=__________.
16.(2019临沂)计算:×﹣tan45°= .
17.(2018深圳)计算:()﹣1﹣2sin45°+|﹣|+(2018﹣π)0.
18.(2018常州)计算:|﹣1|﹣﹣(1﹣)0+4sin30°.
19.(2018菏泽)计算:.
20.(2018孝感)计算
21.计算:
答案与提示
1、D 2、A 3、A 4、B 5、D 6、A 7、D 8、D
9、 10、 11、 12、2 13、 14、 15、
1、解:∵∠DAB=∠DEB,∴tan∠DAB=tan∠DEB=.
2、由勾股定理得:BC=6 sinA==
3、由勾股定理得:AB=5,sinB==
4、解:连接BC,由网格可得AB=BC=,AC=,即AB2+BC2=AC2,
∴△ABC为等腰直角三角形,∴∠BAC=45°,则tan∠BAC=1,故选:B.
4题图 8题图 9题图 12题图 15题图
6、解:∵四边形ABCD是矩形,∴AD=BC,AD∥BC,
∵点E是边BC的中点,∴BE=BC=AD,∴△BEF∽△DAF,
∴=,∴EF=AF,∴EF=AE,
∵点E是边BC的中点,∴由矩形的对称性得:AE=DE,∴EF=DE,设EF=x,则DE=3x,
∴DF==2x,∴tan∠BDE===;故选:A.
7、解:由作图可知:AC=AB=BC,∴△ABC是等边三角形,由作图可知:CB=CA=CD,
∴点C是△ABD的外心,∠ABD=90°,BD=AB,∴S△ABD=AB2,
∵AC=CD,∴S△BDC=AB2,故A、B、C正确,故选D.
8、如图,过C作CD⊥AB于D,则∠ADC=90°,∴AC===5.∴sin∠BAC==.
9、解:如图所示:∵∠C=90°,tanA=,∴设BC=x,则AC=2x,故AB=x,
则sinB===.故答案为:.
10、解:∵AB2=32+42=25、AC2=22+42=20、BC2=12+22=5,∴AC2+BC2=AB2,
∴△ABC为直角三角形,且∠ACB=90°,则sin∠BAC==,故答案为:.
11、解:由折叠知,A'E=AE,A'B=AB=6,∠BA'E=90°,∴∠BA'C=90°,
在Rt△A'CB中,A'C==8,
设AE=x,则A'E=x,∴DE=10﹣x,CE=A'C+A'E=8+x,
在Rt△CDE中,根据勾股定理得,(10﹣x)2+36=(8+x)2, ∴x=2, ∴AE=2,
在Rt△ABE中,根据勾股定理得,BE==2,
∴sin∠ABE==,故答案为:.
12、解:如图,连接BE,∵四边形BCEK是正方形,
∴KF=CF=CK,BF=BE,CK=BE,BE⊥CK,∴BF=CF,
根据题意得:AC∥BK,∴△ACO∽△BKO,∴KO:CO=BK:AC=1:3,∴KO:KF=1:2,
∴KO=OF=CF=BF,
在Rt△PBF中,tan∠BOF==2,∵∠AOD=∠BOF,∴tan∠AOD=2.故答案为:2
13、解:∵旗杆高AB=8m,旗杆影子长BC=16m,∴tanC=,故答案为:
14、解:观察可知,正切值的分子是3,5,7,9,…,2n+1,
分母与勾股数有关系,分别是勾股数3,4,5;5,12,13;7,24,25;9,40,41;…,2n+1,,中的中间一个.
∴tanαn==.故答案为:.
15、如图,过B作BD⊥AC于D,∵∠A=45°,∴∠ABD=∠A=45°,∴AD=BD.
∵∠ADB=∠CDB=90°,∴AB2=AD2+DB2=2BD2,BC2=DC2+BD2,
∴AC2–BC2=(AD+DC)2–(DC2+BD2)=AD2+DC2+2AD?DC–DC2–BD2=2AD?DC=2BD?DC,
∵AC2–BC2AB2,∴2BD?DC2BD2,
∴DCBD,∴.故答案为:.
二、特殊角的三角函数值
1、C 2、A 3、A 4、C 5、A 6、D 7、(﹣1,)8、 9、2 10、1+ 11、60°12、 13、 14、1﹣ 15、0 16、-1
4、锐角三角函数计算,2sin60°=2×=,故选C.
5、∵∠α为锐角,且sinα=,∴∠α=30°.故选A.
6、解:如图,连接AM,
∵将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB'C′D′,
∴AD=AB′=1,∠BAB′=30°,∴∠B′AD=60°,
在Rt△ADM和Rt△AB′M中,
∵,∴Rt△ADM≌Rt△AB′M(HL),∴∠DAM=∠B′AM=∠B′AD=30°,
∴DM=ADtan∠DAM=1×=,∴点M的坐标为(﹣1,),故答案为:(﹣1,).
6题图 8题图 12题图
8、解:设圆的圆心为点O,能够将△ABC完全覆盖的最小圆是△ABC的外接圆,
∵在△ABC中,∠A=60°,BC=5cm,∴∠BOC=120°,
作OD⊥BC于点D,则∠ODB=90°,∠BOD=60°,∴BD=,∠OBD=30°,
∴OB=,得OB=,∴2OB=,
即△ABC外接圆的直径是cm, 故答案为:.
11、依题意,得2sinα+1×(﹣)=0,解得sinα=.∵α是锐角,∴α=60°.
12.(2019?东营)解:∵点M,N分别是BC,AC的中点,∴MN=AB,
∴当AB取得最大值时,MN就取得最大值,当AB是直径时,AB最大,
连接AO并延长交⊙O于点B′,连接CB′,
∵AB′是⊙O的直径,∴∠ACB′=90°.
∵∠ABC=45°,AC=5,∴∠AB′C=45°,
∴AB′===5,∴MN最大=.故答案为:.
13.(2019?潍坊)解:∵四边形ABCD为矩形,∴∠ADC=∠C=∠B=90°,AB=DC,
由翻折知,△AED≌△A'ED,△A'BE≌△A'B'E,∠A'B'E=∠B=∠A'B'D=90°,
∴∠AED=∠A'ED,∠A'EB=∠A'EB',BE=B'E,∴∠AED=∠A'ED=∠A'EB=×180°=60°,
∴∠ADE=90°﹣∠AED=30°,∠A'DE=90°﹣∠A'EB=30°,
∴∠ADE=∠A'DE=∠A'DC=30°,
又∵∠C=∠A'B'D=90°,DA'=DA',∴△DB'A'≌△DCA'(AAS),∴DC=DB',
在Rt△AED中,∠ADE=30°,AD=2,
∴AE==, 设AB=DC=x,则BE=B'E=x﹣
∵AE2+AD2=DE2, ∴()2+22=(x+x﹣)2,
解得,x1=(负值舍去),x2=, 故答案为:.
14、原式=2﹣+1﹣﹣=1﹣.故答案为:1﹣.
15、原式=1–2×=1–1=0,故答案为:0.
17、=2-2++1=3
18、=1-2-1+4=1-2-1+2=0
19、=-1+4-(2-)-2=5-2+-=3
20、=9+4+2-4=9+4+2-2=13
21、
