北师大版八年级数学下册1.3线段的垂直平分线课件(共18张PPT)
文档属性
| 名称 | 北师大版八年级数学下册1.3线段的垂直平分线课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 652.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
北师大版八年级(下)
1.3线段的垂直平分线
第一章 三角形的证明
第1课时 线段垂直平分线的性质与判定
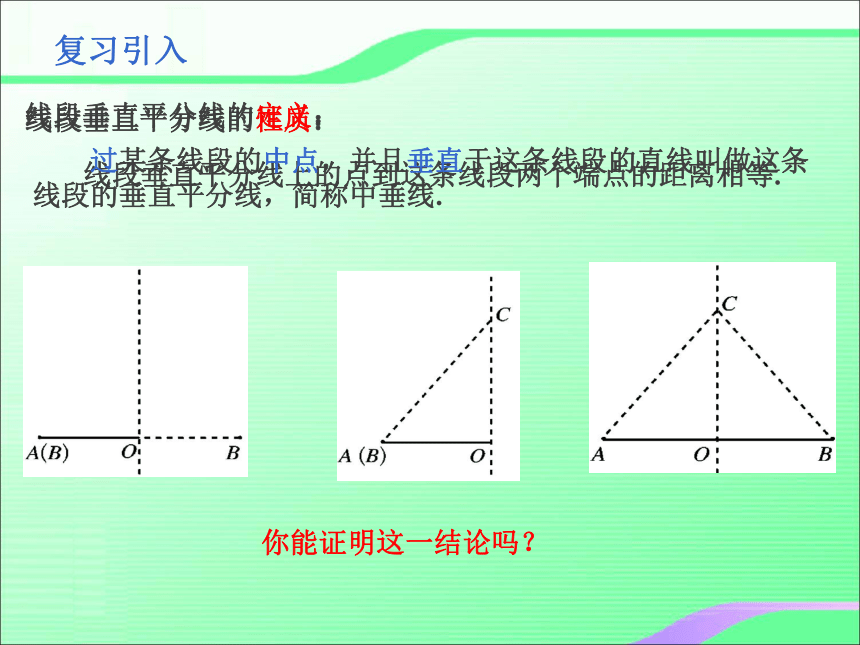
复习引入
线段垂直平分线的性质:
你能证明这一结论吗?
线段垂直平分线上的点到这条线段两个端点的距离相等.
线段垂直平分线的定义:
过某条线段的中点,并且垂直于这条线段的直线叫做这条
线段的垂直平分线,简称中垂线.
北师大版八年级(下)
1.3线段的垂直平分线
第一章 三角形的证明
第1课时 线段垂直平分线的性质与判定
学习目标
1.会证明线段的垂直平分线的性质定理及判定定理。
2.能运用线段垂直平分线的性质定理和判定定理解决问题。
学案讨论
重点讨论
探究二:线段中垂线的判定定理的证明方法.
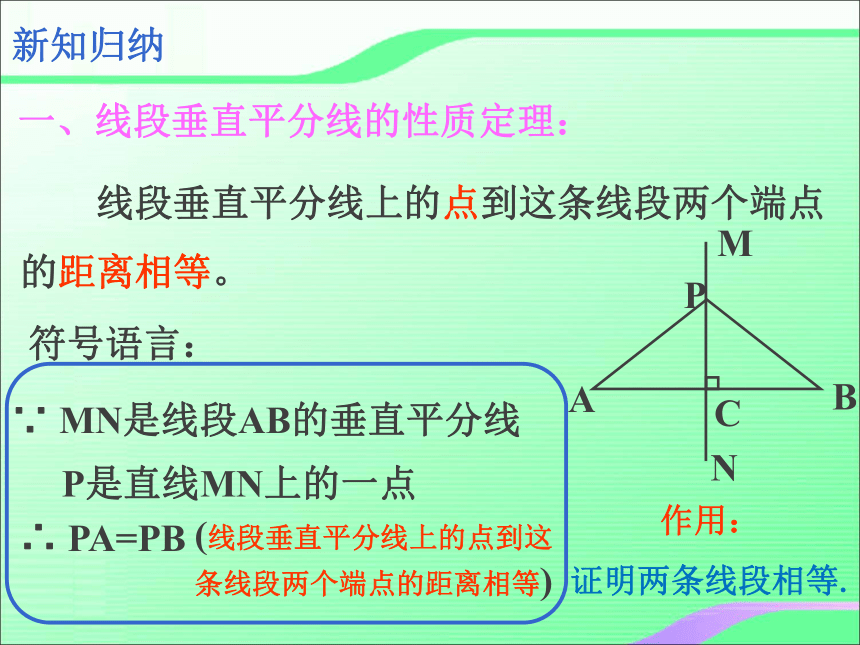
新知归纳
一、线段垂直平分线的性质定理:
线段垂直平分线上的点到这条线段两个端点
的距离相等。
符号语言:
∵ MN是线段AB的垂直平分线
∴ PA=PB
(线段垂直平分线上的点到这
条线段两个端点的距离相等)
作用:
证明两条线段相等.
P是直线MN上的一点
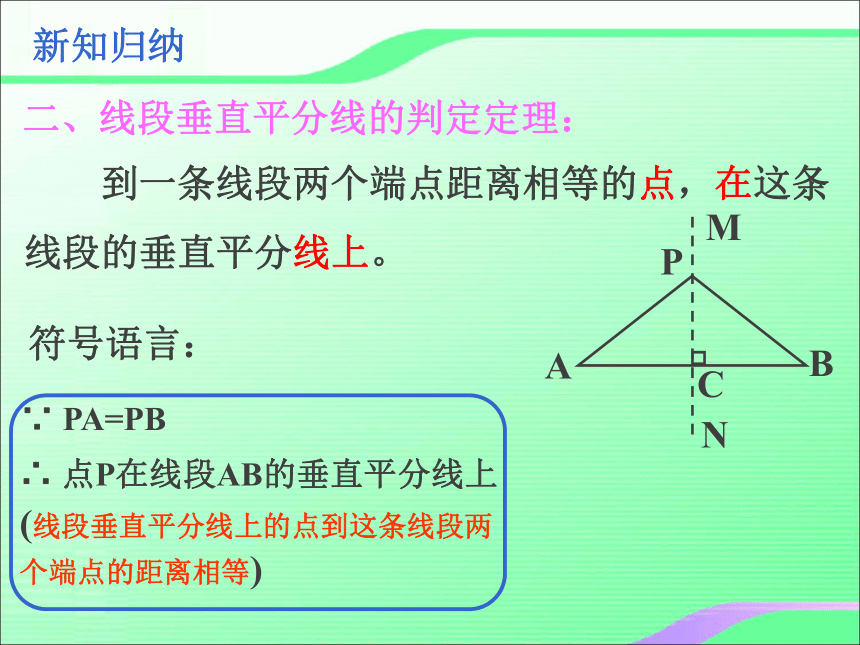
新知归纳
二、线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条
线段的垂直平分线上。
符号语言:
∵ PA=PB
∴ 点P在线段AB的垂直平分线上
(线段垂直平分线上的点到这条线段两
个端点的距离相等)
已知:如图,PA=PB。
求证:点P在线段AB的垂直平分线上。
证明:
新知探究
过点P作PO⊥AB,垂足为O
∵ PO⊥AB
∴ ∠POA=∠POB=90°
在Rt△AOP和Rt△BOP中
PA=PB
PO=PO
∴ Rt△APO≌Rt△BPO(HL)
∴ AO=BO(全等三角形的对应边相等)
∴ P在AB的垂直平分线上.
方法一:做垂线,证中点
已知:如图,PA=PB。
求证:点P在线段AB的垂直平分线上。
证明:
把线段AB的中点记为O,连接PO
∵O为AB的中点
∴AO=BO
在△AOP和△BOP中
新知探究
PA=PB
PO=PO
AO=BO
∴ △APO≌△BPO(SSS)
∴∠POA=∠POB=90°
∴P在AB的垂直平分线上.
∴PO⊥AB
方法二:做中点,证垂直
已知:如图,PA=PB。
求证:点P在线段AB的垂直平分线上。
证明:
过点P作PO⊥AB于点O
∵PA=PB ,PO⊥AB
∴PO平分线段AB
∴PO垂直平分线段AB
即点P在段线AB垂直平分线上
新知探究
方法三:等腰三角形的“三线合一”
新知归纳
二、线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条
线段的垂直平分线上。
符号语言:
∵ PA=PB
∴ 点P在线段AB的垂直平分线上
(线段垂直平分线上的点到这条线段两
个端点的距离相等)
作用:
证明点在直线上
(或直线经过某一点)
例:已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC.
求证:直线OA垂直平分线段BC.
例题剖析
证明:
∵ AB=AC
∴ 点A在线段BC的垂直平分线上
(到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上).
同理,点O在线段BC的垂直平分线上
∴ 直线AO是线段BC的垂直平分
(两点确定一条直线).
1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,
如果EC=7cm,那么ED= cm;
如果∠ECD=60°,那么∠EDC= .
7
60°
随堂练习
2.已知:如图AB=AC,BD=CD,P是AD上一点.
求证:PB=PC.
证明:连接BC,
∵AB=AC,BD=CD,
∴点A,D在线段BC的垂直平分线上;
∴直线AD垂直平分线段BC,
∴PB=PC.
随堂练习
1.如图,在△ABC中,AB=AC,∠BAC=120°,AB
的垂直平分线交AB于点E,交BC于点F,连接AF,
求∠AFC的度数.
巩固提升
2.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长.
解:∵DE为AB的垂直平分线
∴AE=BE
∵△BCE的周长等于50
∴BE+EC+BC=50
即:AE+EC+BC=50
∴AC+BC=50
∵AC=27
∴BC=23
比一比:你的写作过程完整吗?
巩固提升
课堂小结
能力
知 识
收 获
学科思想
当堂检测
北师大版八年级(下)
1.3线段的垂直平分线
第一章 三角形的证明
第1课时 线段垂直平分线的性质与判定
复习引入
线段垂直平分线的性质:
你能证明这一结论吗?
线段垂直平分线上的点到这条线段两个端点的距离相等.
线段垂直平分线的定义:
过某条线段的中点,并且垂直于这条线段的直线叫做这条
线段的垂直平分线,简称中垂线.
北师大版八年级(下)
1.3线段的垂直平分线
第一章 三角形的证明
第1课时 线段垂直平分线的性质与判定
学习目标
1.会证明线段的垂直平分线的性质定理及判定定理。
2.能运用线段垂直平分线的性质定理和判定定理解决问题。
学案讨论
重点讨论
探究二:线段中垂线的判定定理的证明方法.
新知归纳
一、线段垂直平分线的性质定理:
线段垂直平分线上的点到这条线段两个端点
的距离相等。
符号语言:
∵ MN是线段AB的垂直平分线
∴ PA=PB
(线段垂直平分线上的点到这
条线段两个端点的距离相等)
作用:
证明两条线段相等.
P是直线MN上的一点
新知归纳
二、线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条
线段的垂直平分线上。
符号语言:
∵ PA=PB
∴ 点P在线段AB的垂直平分线上
(线段垂直平分线上的点到这条线段两
个端点的距离相等)
已知:如图,PA=PB。
求证:点P在线段AB的垂直平分线上。
证明:
新知探究
过点P作PO⊥AB,垂足为O
∵ PO⊥AB
∴ ∠POA=∠POB=90°
在Rt△AOP和Rt△BOP中
PA=PB
PO=PO
∴ Rt△APO≌Rt△BPO(HL)
∴ AO=BO(全等三角形的对应边相等)
∴ P在AB的垂直平分线上.
方法一:做垂线,证中点
已知:如图,PA=PB。
求证:点P在线段AB的垂直平分线上。
证明:
把线段AB的中点记为O,连接PO
∵O为AB的中点
∴AO=BO
在△AOP和△BOP中
新知探究
PA=PB
PO=PO
AO=BO
∴ △APO≌△BPO(SSS)
∴∠POA=∠POB=90°
∴P在AB的垂直平分线上.
∴PO⊥AB
方法二:做中点,证垂直
已知:如图,PA=PB。
求证:点P在线段AB的垂直平分线上。
证明:
过点P作PO⊥AB于点O
∵PA=PB ,PO⊥AB
∴PO平分线段AB
∴PO垂直平分线段AB
即点P在段线AB垂直平分线上
新知探究
方法三:等腰三角形的“三线合一”
新知归纳
二、线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条
线段的垂直平分线上。
符号语言:
∵ PA=PB
∴ 点P在线段AB的垂直平分线上
(线段垂直平分线上的点到这条线段两
个端点的距离相等)
作用:
证明点在直线上
(或直线经过某一点)
例:已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC.
求证:直线OA垂直平分线段BC.
例题剖析
证明:
∵ AB=AC
∴ 点A在线段BC的垂直平分线上
(到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上).
同理,点O在线段BC的垂直平分线上
∴ 直线AO是线段BC的垂直平分
(两点确定一条直线).
1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,
如果EC=7cm,那么ED= cm;
如果∠ECD=60°,那么∠EDC= .
7
60°
随堂练习
2.已知:如图AB=AC,BD=CD,P是AD上一点.
求证:PB=PC.
证明:连接BC,
∵AB=AC,BD=CD,
∴点A,D在线段BC的垂直平分线上;
∴直线AD垂直平分线段BC,
∴PB=PC.
随堂练习
1.如图,在△ABC中,AB=AC,∠BAC=120°,AB
的垂直平分线交AB于点E,交BC于点F,连接AF,
求∠AFC的度数.
巩固提升
2.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长.
解:∵DE为AB的垂直平分线
∴AE=BE
∵△BCE的周长等于50
∴BE+EC+BC=50
即:AE+EC+BC=50
∴AC+BC=50
∵AC=27
∴BC=23
比一比:你的写作过程完整吗?
巩固提升
课堂小结
能力
知 识
收 获
学科思想
当堂检测
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
