六年级上册数学课件-第1课时 圆的认识(一)人教版(共17张PPT)
文档属性
| 名称 | 六年级上册数学课件-第1课时 圆的认识(一)人教版(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 19:52:42 | ||
图片预览





文档简介
(共14张PPT)
圆的认识(一)
探究新知
基础练习
拓展练习
课堂小结
数学阅读
人教版数学六年级上册 第五单元
复习导入
复习导入
说说生活中的“圆”。
生活中的“圆”随处可见,请同学们自己说一说见过哪些圆形的东西?
(一)画圆中感受“圆”
你能想办法在纸上画一个圆吗?
探究新知
探究新知
用圆规画“圆”
探究新知
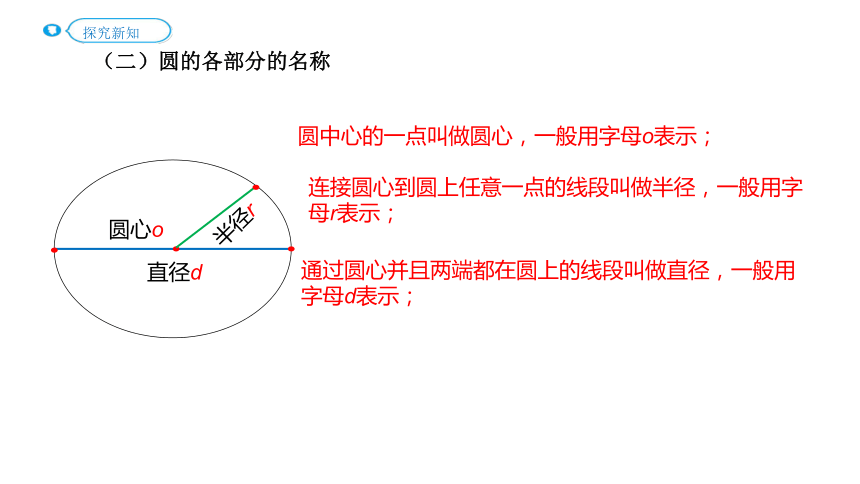
(二)圆的各部分的名称
圆中心的一点叫做圆心,一般用字母o表示;
圆心o
半径r
直径d
连接圆心到圆上任意一点的线段叫做半径,一般用字母r表示;
通过圆心并且两端都在圆上的线段叫做直径,一般用字母d表示;
探究新知
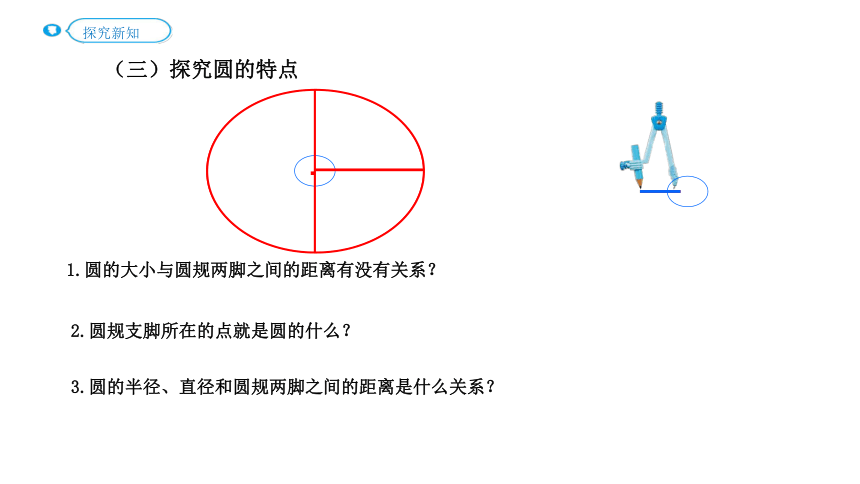
(三)探究圆的特点
.
1.圆的大小与圆规两脚之间的距离有没有关系?
2.圆规支脚所在的点就是圆的什么?
3.圆的半径、直径和圆规两脚之间的距离是什么关系?
把在纸上画好的圆剪下来,对折、打开,再换个方向对折、打开,反复这样折几次。
探究新知
圆心
(2)用尺子量一量,这些折痕的长度一样吗?这些折痕是圆的什么?
(1)这些折痕相交点有什么特点和规律?这个相交点应该是圆的什么?用尺子量一下这个点到圆上的任意一点的距离,你会发现什么?
所有的折痕长度都是一样的,这些折痕就是圆的直径。圆的直径就是通过圆心并且两条交端在圆上的线段。
所有的折痕都会相交在唯一一个点上,这个点就是圆的圆心。这个点到圆上的任意一点的距离是相同的。所以圆心就是圆的中心,是到圆上任意一点距离都相等的一个点。
d
直径
1.认识直径和半径的关系
O
把在纸上画好的圆剪下来,对折、打开,再换个方向对折、打开,反复这样折几次。
探究新知
圆心
一个圆里有无数条半径。
(3)一个圆里,到底有几条直径?
d
直径
只要过圆心并且两端都在圆上的线段, 都是圆的直径,这样的线段有无数条。
(4)连接圆心到圆上任意一点,这条线段是圆的什么?量一下这条线段的长度,再和圆的直径作比较,你会发现什么?
连接圆心到圆上任意一点的线段就是圆的半径,圆的半径长度正好是圆的直径长度的一半。
(5)一个圆里,有多少条半径?
r
半径
O
o
r
2.认识圆心和半径的作用
圆的中心位置由什么决定的?半径决定圆的什么?
圆心确定了,圆的中心位置就确定了。半径决定了圆的大小。
探究新知
基础练习
1.说说圆上各部分的名称及它们的含义。
圆心
O
直径
d
半径
r
(1)到圆上任意一点的距离都相等的点,就是这个圆的圆心。换句话说,圆心到圆上任意一点的距离都相等。圆心只有一个。
(2)过圆心且两端都在圆上的线段,就是圆的直径,一个圆内可以画出无数条直径。而且这些直径全部相等。
(3)连接圆心到圆上的任意一点的线段,就是圆的半径,一个圆内可以画出无数条半径。而且这些半径全部相等。两个半径的长度相当于一个直径的长度,直径长度的二分之一就是半径的长度。
o
6 cm
d =______
o
10cm
d =______
o
高3.5cm
r =______
3 cm
10cm
3.5cm
6 cm
2、看图填空。
r =_____
3 cm
o
基础练习
基础练习
3.判断对错,并说说为什么。
(1)圆的直径是圆的半径的2倍。( )
(2)一个圆的圆心有无数个。( )
(3)一个圆有无数条直径和无数条半径。( )
(4)右图中线段 d是这个圆的直径。( )
(5)右图中线段 r是这个圆的半径。( )
(6)圆心决定圆的位置,半径决定圆的大小。( )
(7)要画直径2厘米的圆,圆规两脚间的距离就是2厘米。( )
×
√
×
×
×
√
×
d
r
请你想办法找出下面圆的圆心。说一说你是怎么找到的。
拓展练习
A
B
1.任意画一条线段AB。
3.找到线段AB的中点并作垂线。
2.再任意画一条线段CD。
C
D
4.找到线段CD 的中点并作垂线。
5.两条垂线相交的点就是圆心。
O
数学阅读
会作圆,但不一定就懂得圆的性质。古代埃及人就认为:圆,是神赐给 人的神圣图形。一直到两千多年前我国的墨子(约公元前468-前376年)才给圆下了一个定义:圆,一中同长也。
意思是说:圆有一个圆心,圆心到圆周的长都相等。这个定义比希腊数学家欧几里得(约公元前330-前275年)给圆下定义要早100年。
圆的概念是怎样形成的
古代人最早是从太阳、阴历十五的月亮得到圆的概念的。
在一万八千年前的山顶洞人曾经在兽牙、砾石和石珠上钻孔,那些孔有的就很像圆。到了陶器时代,许多陶器都是圆的。圆的陶器是将泥土放在一个转盘上制成的。当人们开始纺线,又制出了圆形的石纺锤或陶纺锤。古代人还发现搬运圆的木头时滚着走比较省劲。后来他们在搬运重物的时候,就把几段圆木垫在大树、大石头下面滚着走,这样当然比扛着走省劲得多。
约在6000年前,美索不达米亚人,做出了世界上第一个轮子——圆型的木盘。大约在4000多年前,人们将圆的木盘固定在木架下,这就成了最初的车子。
圆的认识(一)
探究新知
基础练习
拓展练习
课堂小结
数学阅读
人教版数学六年级上册 第五单元
复习导入
复习导入
说说生活中的“圆”。
生活中的“圆”随处可见,请同学们自己说一说见过哪些圆形的东西?
(一)画圆中感受“圆”
你能想办法在纸上画一个圆吗?
探究新知
探究新知
用圆规画“圆”
探究新知
(二)圆的各部分的名称
圆中心的一点叫做圆心,一般用字母o表示;
圆心o
半径r
直径d
连接圆心到圆上任意一点的线段叫做半径,一般用字母r表示;
通过圆心并且两端都在圆上的线段叫做直径,一般用字母d表示;
探究新知
(三)探究圆的特点
.
1.圆的大小与圆规两脚之间的距离有没有关系?
2.圆规支脚所在的点就是圆的什么?
3.圆的半径、直径和圆规两脚之间的距离是什么关系?
把在纸上画好的圆剪下来,对折、打开,再换个方向对折、打开,反复这样折几次。
探究新知
圆心
(2)用尺子量一量,这些折痕的长度一样吗?这些折痕是圆的什么?
(1)这些折痕相交点有什么特点和规律?这个相交点应该是圆的什么?用尺子量一下这个点到圆上的任意一点的距离,你会发现什么?
所有的折痕长度都是一样的,这些折痕就是圆的直径。圆的直径就是通过圆心并且两条交端在圆上的线段。
所有的折痕都会相交在唯一一个点上,这个点就是圆的圆心。这个点到圆上的任意一点的距离是相同的。所以圆心就是圆的中心,是到圆上任意一点距离都相等的一个点。
d
直径
1.认识直径和半径的关系
O
把在纸上画好的圆剪下来,对折、打开,再换个方向对折、打开,反复这样折几次。
探究新知
圆心
一个圆里有无数条半径。
(3)一个圆里,到底有几条直径?
d
直径
只要过圆心并且两端都在圆上的线段, 都是圆的直径,这样的线段有无数条。
(4)连接圆心到圆上任意一点,这条线段是圆的什么?量一下这条线段的长度,再和圆的直径作比较,你会发现什么?
连接圆心到圆上任意一点的线段就是圆的半径,圆的半径长度正好是圆的直径长度的一半。
(5)一个圆里,有多少条半径?
r
半径
O
o
r
2.认识圆心和半径的作用
圆的中心位置由什么决定的?半径决定圆的什么?
圆心确定了,圆的中心位置就确定了。半径决定了圆的大小。
探究新知
基础练习
1.说说圆上各部分的名称及它们的含义。
圆心
O
直径
d
半径
r
(1)到圆上任意一点的距离都相等的点,就是这个圆的圆心。换句话说,圆心到圆上任意一点的距离都相等。圆心只有一个。
(2)过圆心且两端都在圆上的线段,就是圆的直径,一个圆内可以画出无数条直径。而且这些直径全部相等。
(3)连接圆心到圆上的任意一点的线段,就是圆的半径,一个圆内可以画出无数条半径。而且这些半径全部相等。两个半径的长度相当于一个直径的长度,直径长度的二分之一就是半径的长度。
o
6 cm
d =______
o
10cm
d =______
o
高3.5cm
r =______
3 cm
10cm
3.5cm
6 cm
2、看图填空。
r =_____
3 cm
o
基础练习
基础练习
3.判断对错,并说说为什么。
(1)圆的直径是圆的半径的2倍。( )
(2)一个圆的圆心有无数个。( )
(3)一个圆有无数条直径和无数条半径。( )
(4)右图中线段 d是这个圆的直径。( )
(5)右图中线段 r是这个圆的半径。( )
(6)圆心决定圆的位置,半径决定圆的大小。( )
(7)要画直径2厘米的圆,圆规两脚间的距离就是2厘米。( )
×
√
×
×
×
√
×
d
r
请你想办法找出下面圆的圆心。说一说你是怎么找到的。
拓展练习
A
B
1.任意画一条线段AB。
3.找到线段AB的中点并作垂线。
2.再任意画一条线段CD。
C
D
4.找到线段CD 的中点并作垂线。
5.两条垂线相交的点就是圆心。
O
数学阅读
会作圆,但不一定就懂得圆的性质。古代埃及人就认为:圆,是神赐给 人的神圣图形。一直到两千多年前我国的墨子(约公元前468-前376年)才给圆下了一个定义:圆,一中同长也。
意思是说:圆有一个圆心,圆心到圆周的长都相等。这个定义比希腊数学家欧几里得(约公元前330-前275年)给圆下定义要早100年。
圆的概念是怎样形成的
古代人最早是从太阳、阴历十五的月亮得到圆的概念的。
在一万八千年前的山顶洞人曾经在兽牙、砾石和石珠上钻孔,那些孔有的就很像圆。到了陶器时代,许多陶器都是圆的。圆的陶器是将泥土放在一个转盘上制成的。当人们开始纺线,又制出了圆形的石纺锤或陶纺锤。古代人还发现搬运圆的木头时滚着走比较省劲。后来他们在搬运重物的时候,就把几段圆木垫在大树、大石头下面滚着走,这样当然比扛着走省劲得多。
约在6000年前,美索不达米亚人,做出了世界上第一个轮子——圆型的木盘。大约在4000多年前,人们将圆的木盘固定在木架下,这就成了最初的车子。
