2020版新教材高中数学第二章等式与不等式2.1.1等式的性质与方程的解集课件新人教B版必修1:67张PPT
文档属性
| 名称 | 2020版新教材高中数学第二章等式与不等式2.1.1等式的性质与方程的解集课件新人教B版必修1:67张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览



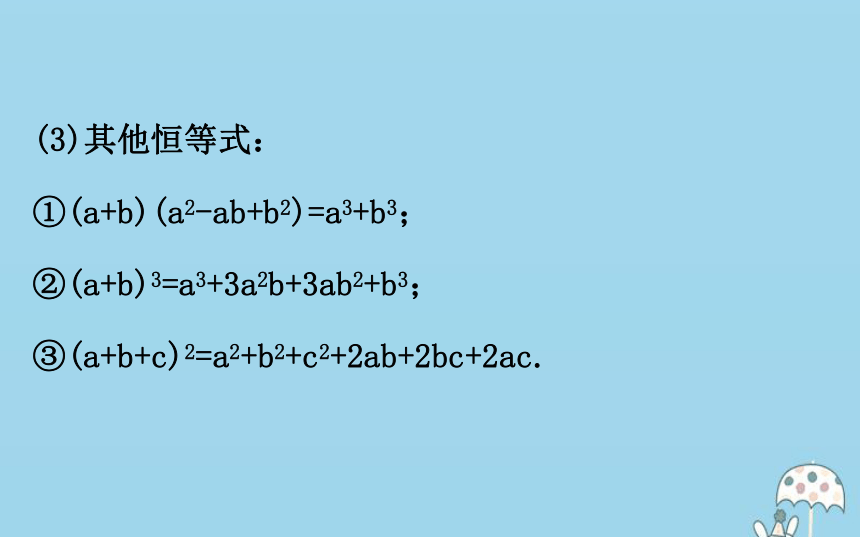








文档简介
课件67张PPT。第二章 等式与不等式
2.1 等 式
2.1.1 等式的性质与方程的解集 1.常用乘法公式
(1)平方差公式:(a+b)(a-b)=a2-b2,两个数的和与这两个数的差的积等于这两个数的平方差.
(2)完全平方公式:(a±b)2=a2±2ab+b2,两数和(或差)的平方,等于这两数的平方和,加上(或减去)这两数积的2倍.(3)其他恒等式:
①(a+b)(a2-ab+b2)=a3+b3;
②(a+b)3=a3+3a2b+3ab2+b3;
③(a+b+c)2=a2+b2+c2+2ab+2bc+2ac.【思考】
(1)平方差公式的左右两边分别有什么特点?
提示:公式的左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;右边是相同项的平方减去相反项的平方.(2)完全平方公式的左右两边分别有什么特点?
提示:公式左边都是二项式的平方,右边是一个二次三项式;公式右边第一、三项分别是左边第一、第二项的平方;第二项是左边两项积的2倍.2.十字相乘法
(1)二次项系数为1时:
x2+(a+b)x+ab=(x+a)(x+b)
(2)二次系数不为1时:
acx2+(ad+bc)x+bd=(ax+b)(cx+d)
(3)记忆口诀:拆两头,凑中间.【思考】
十字相乘法分解因式的关键是什么?
提示:把二次项和常数项分解,交叉相乘,得到两个因数,再把两个因式相加,看它们的和是不是正好等于一次项系数.3.方程的解集:
(1)方程的解(根):能使方程左右两边相等的未知数的值.
(2)方程的解集:一个方程所有的解组成的集合.【思考】
把方程通过适当变换后,求出的未知数的值都是这个方程的解(根)吗?
提示:把方程通过变换,求出的未知数的值不一定是这个方程的根,也可能是这个方程的增根.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)计算(2a+5)(2a-5)=2a2-25. ( )
(2)因式分解过程为:x2-3xy-4y2=(x+y)(x-4). ( )
(3)用因式分解法解方程时部分过程为:
(x+2)(x-3)=6,所以x+2=3或x-3=2. ( )提示:(1)×.(2a+5)(2a-5)=(2a)2-25=4a2-25.
(2)×.x2-3xy-4y2=(x+y)(x-4y).
(3)×.若(x+2)(x-3)=0,可化为x+2=0或x-3=0.2.方程x(x-1)=x的根是 ( )
A.x=2 B.x=-2
C.x1=-2,x2=0 D.x1=2,x2=0
【解析】选D.因为x(x-1)=x,所以x2-x=x,
所以x2-2x=0,所以x(x-2)=0,所以x1=2,x2=0.3.(多选题)下列等式中,是恒等式的是 ( )
A.(x-2)(x+2)=x2-4
B.(a-b)2=a2-2ab+b2
C.(-3+m)·(3+m)=m2-9
D.16x2-9=24x【解析】选A、B、C.A中,(x-2)·(x+2)=x2-4,
使用平方差公式化简,是恒等式;B中,(a-b)2
=a2-2ab+b2,使用完全平方公式化简,是恒等式;
C中,(-3+m)(3+m)=(m-3)(m+3)=m2-9,
平方差公式化简,是恒等式;
D中,16x2-9=24x是方程,不是恒等式.类型一 常用乘法公式的应用
【典例】1.化简(m2+1)(m+1)(m-1)-(m4+1)的值
是 ( )
A.-2m2 B.0 C.-2 D.-12.计算(x+3y)2-(3x+y)2的结果是 ( )
A.8x2-8y2 B.8y2-8x2
C.8(x+y)2 D.8(x-y)2【思维·引】
1.先把第一项中的(m+1)(m-1)用平方差公式化简,再和m2+1利用平方差公式化简,最后去括号,合并同类项,化简.2.方法一:先用完全平方公式化简,然后去括号,合并同类项即可;方法二:把x+3y和3x+y分别看作一个整体,利用平方差公式化简.【解析】选C.1.(m2+1)(m+1)(m-1)-(m4+1)
=(m2+1)(m2-1)-(m4+1)
=(m4-1)-(m4+1)=m4-1-m4-1=-2.2.选B.方法一:(x+3y)2-(3x+y)2
=x2+6xy+9y2-(9x2+6xy+y2)
=x2+6xy+9y2-9x2-6xy-y2
=8y2-8x2.方法二:
(x+3y)2-(3x+y)2
=[(x+3y)+(3x+y)][(x+3y)-(3x+y)]
=(x+3y+3x+y)(x+3y-3x-y)
=(4x+4y)(-2x+2y)=4(x+y)×2(-x+y)
=8y2-8x2.【内化·悟】
1.利用数学公式化简,公式中的a,b是一个代数式时,怎么处理?
提示:当公式中的a,b是一个代数式时,利用整体代入思想,把代数式看作一个整体代入即可.2.一个题目中要应用多个公式时,怎样选择公式使用顺序?
提示:当一个题目中要使用多个数学公式时,我们要根据题目特点适当选择公式,尽可能将运算简化.【类题·通】
(1)使用公式化简时,一定要分清公式中的a,b分别对应题目中的哪个数或哪个整式.
(2)利用公式化简时,要注意选择公式,公式选择恰当,可以有效地简化运算.【习练·破】
1.如果(a-b-3)(a-b+3)=40,那么a-b的值为 ( )
A.49 B.7 C.-7 D.7或-7
【解析】选D.(a-b-3)(a-b+3)=(a-b)2-9=40,
即(a-b)2=49,则a-b=±7.2.已知a2+b2+2a-4b+5=0,则2a2+4b-3的值为________.?
【解析】a2+b2+2a-4b+5=(a2+2a+1)+(b2-4b+4)
=(a+1)2+(b-2)2=0,所以a=-1,b=2,
所以2a2+4b-3=2×(-1)2+4×2-3=7.
答案:7类型二 十字相乘法分解因式
【典例】把下列各式因式分解.
(1)x2+3x+2
(2)6x2-7x-5
(3)5x2+6xy-8y2【思维·引】
(1)x2+3x+2的二次项的系数是1,常数项2=1×2,一次项系数3=1+2,这是一个x2+(p+q)x+pq型式子.(2)6x2-7x-5的二次项系数是6=2×3,常数项-5
=1×(-5),一次项系数-7=2×(-5)+3×1,这是一个acx2+(ad+bc)x+bd型式子,因此可用公式acx2+(ad+bc)x+bd=(ax+b)(cx+d)分解因式.(3)5x2+6xy-8y2的二次项系数是5=1×5,常数项
-8y2=2y×(-4y),一次项系数6y=1×(-4y)+5×(2y),这也是一个acx2+(ad+bc)x+bd型式子,因此可用公式acx2+(ad+bc)x+bd=(ax+b)(cx+d)分解因式.【解析】(1)x2+3x+2=(x+1)(x+2)
1×2+1×1=3(2)6x2-7x-5=(2x+1)(3x-5)
2×(-5)+3×1=-7(3)5x2+6xy-8y2=(x+2y)(5x-4y)
1×(-4y)+5×(2y)=6y【内化·悟】
利用十字相乘法分解因式时,怎样把二次项和常数项分解?提示:当二次项系数为负数时,先提出负号,使二次项系数为正数,然后再看常数项;常数项为正数时,应分解为两同号因数,它们的符号与一次项系数的符号相同;常数项为负数时,应将它分解为两异号因数,使十字连线上两数之积绝对值较大的一组与一次项系数的符号相同.【类题·通】
十字相乘法因式分解的形式
尝试把某些二次三项式如ax2+bx+c分解因式,先把a分解成a=a1a2,把c分解成c=c1c2,并且排列如下:这里按斜线交叉相乘的积的和就是a1c2+a2c1,如果它正好等于二次三项式ax2+bx+c中一次项的系数b,那么ax2+bx+c就可以分解成(a1x+c1)(a2x+c2),其中a1,c1是上图中上面一行的两个数,a2,c2是下面一行的两个数.【习练·破】
1.x2+10x+16分解因式为 ( )
A.(x+2)(x+8) B.(x-2)(x+8)
C.(x+2)(x-8) D.(x-2)(x-8)【解析】选A.x2+10x+16=(x+2)(x+8).
1×8+1×2=102.x2-13xy-30y2分解因式为 ( )
A.(x-3y)(x-10y) B.(x+15y)(x-2y)
C.(x+10y)(x+3y) D.(x-15y)(x+2y)【解析】选D.x2-13xy-30y2=(x-15y)(x+2y)
1×2y+1×(-15y)=-13y3.6x2-29x+35分解因式为 ( )
A.(2x-7)(3x-5) B.(3x-7)(2x-5)
C.(3x-7)(2x+5) D.(2x-7)(3x+5)【解析】选B.6x2-29x+35=(3x-7)(2x-5)
3×(-5)+2×(-7)=-29【加练·固】
1.因式分解(x2-7x)2+10(x2-7x)-24.
【解析】(x2-7x)2+10(x2-7x)-24=(x2-7x+12)(x2-7x-2)
=(x-3)(x-4)(x2-7x-2).2.已知a2-ab-6b2=0(a≠0,b≠0),求 的值.【解析】因为a2-ab-6b2=0,所以(a-3b)(a+2b)=0,
所以a=3b或a=-2b,
当a=3b时,
当a=-2b时,
=-2 .类型三 方程的解集
角度1 一元一次方程的解集
【典例】(多选题)下列方程中,解集为{-3}的方程
是 ( )
A. x+1=0 B.2x+1=-8-x
C.3-3x=1 D.2x+6=0【思维·引】
解一元一次方程时,通过移项、合并同类项、系数化为1等过程,解方程.
【解析】选ABD.把x=-3分别代入各选项,只有C选项左右两边的值不相等.角度2 一元二次方程的解集
【典例】求下列方程的解集:
(1)x(x-2)+x-2=0.
(2)x2+5x-6=0.【思维·引】
(1)提取公因式x-2把原方程化为两个因式的积的形式,解方程.
(2)对于二次三项式,一般先采用十字相乘法分解因式,分解因式后再解方程即可.【解析】(1)因式分解,得:(x-2)(x+1)=0.
于是得x-2=0或x+1=0,即x=2或x=-1,因此方程的解集为{-1,2}.(2)分解因式得:x2+5x-6=(x-1)(x+6),1×(-1)+1×6=5因为x2+5x-6=0,
所以(x-1)(x+6)=0,
所以x-1=0或x+6=0,
即x=1或x=-6.
因此方程的解集为{-6,1}. 【类题·通】
利用因式分解法解一元二次方程的步骤:
①将方程的右边化为0;
②将方程的左边进行因式分解;
③令每个因式为0,得到两个一元一次方程;
④解一元一次方程,得到方程的解.【发散·拓】对于二次三项式,采用十字相乘法分解因式时,要注意把二次项系数和常数项分解,交叉相乘,两个因式的和正好等于一次项系数.注意,交叉相乘横着写.【习练·破】
求下列方程的解集:
(1)5x2-2x- =x2-2x+ .
(2)12x2+5x-2=0.【解析】(1)移项、合并同类项,得4x2-1=0.
因式分解,得(2x+1)(2x-1)=0.
于是得2x+1=0或2x-1=0,即x=- 或x= ,
因此方程的解集为 (2)分解因式得:
12x2+5x-2=(3x+2)(4x-1)3×(-1)+4×2=5因为12x2+5x-2=0,
所以(3x+2)(4x-1)=0,
所以3x+2=0或4x-1=0,
即x=- 或x= ,因此方程的解集为 角度3 分类讨论思想的应用
【典例】解方程ax2-(a+1)x+1=0.
【思维·引】把二次项系数分为a=0和a≠0两种情况讨论,第一种情况是解一元一次方程,第二种情况是解一元二次方程.【解析】当a=0时,原方程可化为-x+1=0,
所以x=1,当a≠0时,对于ax2-(a+1)x+1来说,因为a×1=a,
(-1)×(-1)=1,a×(-1)+1×(-1)=-(a+1).如图所示
ax2-(a+1)x+1=(ax-1)(x-1),所以原方程可化为
(ax-1)(x-1)=0,
所以ax-1=0或x-1=0,
所以x= 或x=1.【类题·通】
形如ax2+bx+c=0(含参)的方程的解法
方程的二次项系数中含有参数时,要讨论二次项系数是否可以等于零,当二次项系数等于零时,讨论方程变为一元一次方程或其他情况,当二次项系数不为0时,解一元二次方程.【习练·破】
解方程12x2-ax-a2=0.【解析】当a=0时,原方程可化为:
12x2=0,所以x=0,当a≠0时,因为3×4=12,-a×a
=-a2,3×a+4×(-a)=3a-4a=-a,如图所示所以12x2-ax-a2=(3x-a)(4x+a),
所以原方程可化为(3x-a)(4x+a)=0.
所以3x-a=0或4x+a=0,
所以x1= ,x2=- .
2.1 等 式
2.1.1 等式的性质与方程的解集 1.常用乘法公式
(1)平方差公式:(a+b)(a-b)=a2-b2,两个数的和与这两个数的差的积等于这两个数的平方差.
(2)完全平方公式:(a±b)2=a2±2ab+b2,两数和(或差)的平方,等于这两数的平方和,加上(或减去)这两数积的2倍.(3)其他恒等式:
①(a+b)(a2-ab+b2)=a3+b3;
②(a+b)3=a3+3a2b+3ab2+b3;
③(a+b+c)2=a2+b2+c2+2ab+2bc+2ac.【思考】
(1)平方差公式的左右两边分别有什么特点?
提示:公式的左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;右边是相同项的平方减去相反项的平方.(2)完全平方公式的左右两边分别有什么特点?
提示:公式左边都是二项式的平方,右边是一个二次三项式;公式右边第一、三项分别是左边第一、第二项的平方;第二项是左边两项积的2倍.2.十字相乘法
(1)二次项系数为1时:
x2+(a+b)x+ab=(x+a)(x+b)
(2)二次系数不为1时:
acx2+(ad+bc)x+bd=(ax+b)(cx+d)
(3)记忆口诀:拆两头,凑中间.【思考】
十字相乘法分解因式的关键是什么?
提示:把二次项和常数项分解,交叉相乘,得到两个因数,再把两个因式相加,看它们的和是不是正好等于一次项系数.3.方程的解集:
(1)方程的解(根):能使方程左右两边相等的未知数的值.
(2)方程的解集:一个方程所有的解组成的集合.【思考】
把方程通过适当变换后,求出的未知数的值都是这个方程的解(根)吗?
提示:把方程通过变换,求出的未知数的值不一定是这个方程的根,也可能是这个方程的增根.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)计算(2a+5)(2a-5)=2a2-25. ( )
(2)因式分解过程为:x2-3xy-4y2=(x+y)(x-4). ( )
(3)用因式分解法解方程时部分过程为:
(x+2)(x-3)=6,所以x+2=3或x-3=2. ( )提示:(1)×.(2a+5)(2a-5)=(2a)2-25=4a2-25.
(2)×.x2-3xy-4y2=(x+y)(x-4y).
(3)×.若(x+2)(x-3)=0,可化为x+2=0或x-3=0.2.方程x(x-1)=x的根是 ( )
A.x=2 B.x=-2
C.x1=-2,x2=0 D.x1=2,x2=0
【解析】选D.因为x(x-1)=x,所以x2-x=x,
所以x2-2x=0,所以x(x-2)=0,所以x1=2,x2=0.3.(多选题)下列等式中,是恒等式的是 ( )
A.(x-2)(x+2)=x2-4
B.(a-b)2=a2-2ab+b2
C.(-3+m)·(3+m)=m2-9
D.16x2-9=24x【解析】选A、B、C.A中,(x-2)·(x+2)=x2-4,
使用平方差公式化简,是恒等式;B中,(a-b)2
=a2-2ab+b2,使用完全平方公式化简,是恒等式;
C中,(-3+m)(3+m)=(m-3)(m+3)=m2-9,
平方差公式化简,是恒等式;
D中,16x2-9=24x是方程,不是恒等式.类型一 常用乘法公式的应用
【典例】1.化简(m2+1)(m+1)(m-1)-(m4+1)的值
是 ( )
A.-2m2 B.0 C.-2 D.-12.计算(x+3y)2-(3x+y)2的结果是 ( )
A.8x2-8y2 B.8y2-8x2
C.8(x+y)2 D.8(x-y)2【思维·引】
1.先把第一项中的(m+1)(m-1)用平方差公式化简,再和m2+1利用平方差公式化简,最后去括号,合并同类项,化简.2.方法一:先用完全平方公式化简,然后去括号,合并同类项即可;方法二:把x+3y和3x+y分别看作一个整体,利用平方差公式化简.【解析】选C.1.(m2+1)(m+1)(m-1)-(m4+1)
=(m2+1)(m2-1)-(m4+1)
=(m4-1)-(m4+1)=m4-1-m4-1=-2.2.选B.方法一:(x+3y)2-(3x+y)2
=x2+6xy+9y2-(9x2+6xy+y2)
=x2+6xy+9y2-9x2-6xy-y2
=8y2-8x2.方法二:
(x+3y)2-(3x+y)2
=[(x+3y)+(3x+y)][(x+3y)-(3x+y)]
=(x+3y+3x+y)(x+3y-3x-y)
=(4x+4y)(-2x+2y)=4(x+y)×2(-x+y)
=8y2-8x2.【内化·悟】
1.利用数学公式化简,公式中的a,b是一个代数式时,怎么处理?
提示:当公式中的a,b是一个代数式时,利用整体代入思想,把代数式看作一个整体代入即可.2.一个题目中要应用多个公式时,怎样选择公式使用顺序?
提示:当一个题目中要使用多个数学公式时,我们要根据题目特点适当选择公式,尽可能将运算简化.【类题·通】
(1)使用公式化简时,一定要分清公式中的a,b分别对应题目中的哪个数或哪个整式.
(2)利用公式化简时,要注意选择公式,公式选择恰当,可以有效地简化运算.【习练·破】
1.如果(a-b-3)(a-b+3)=40,那么a-b的值为 ( )
A.49 B.7 C.-7 D.7或-7
【解析】选D.(a-b-3)(a-b+3)=(a-b)2-9=40,
即(a-b)2=49,则a-b=±7.2.已知a2+b2+2a-4b+5=0,则2a2+4b-3的值为________.?
【解析】a2+b2+2a-4b+5=(a2+2a+1)+(b2-4b+4)
=(a+1)2+(b-2)2=0,所以a=-1,b=2,
所以2a2+4b-3=2×(-1)2+4×2-3=7.
答案:7类型二 十字相乘法分解因式
【典例】把下列各式因式分解.
(1)x2+3x+2
(2)6x2-7x-5
(3)5x2+6xy-8y2【思维·引】
(1)x2+3x+2的二次项的系数是1,常数项2=1×2,一次项系数3=1+2,这是一个x2+(p+q)x+pq型式子.(2)6x2-7x-5的二次项系数是6=2×3,常数项-5
=1×(-5),一次项系数-7=2×(-5)+3×1,这是一个acx2+(ad+bc)x+bd型式子,因此可用公式acx2+(ad+bc)x+bd=(ax+b)(cx+d)分解因式.(3)5x2+6xy-8y2的二次项系数是5=1×5,常数项
-8y2=2y×(-4y),一次项系数6y=1×(-4y)+5×(2y),这也是一个acx2+(ad+bc)x+bd型式子,因此可用公式acx2+(ad+bc)x+bd=(ax+b)(cx+d)分解因式.【解析】(1)x2+3x+2=(x+1)(x+2)
1×2+1×1=3(2)6x2-7x-5=(2x+1)(3x-5)
2×(-5)+3×1=-7(3)5x2+6xy-8y2=(x+2y)(5x-4y)
1×(-4y)+5×(2y)=6y【内化·悟】
利用十字相乘法分解因式时,怎样把二次项和常数项分解?提示:当二次项系数为负数时,先提出负号,使二次项系数为正数,然后再看常数项;常数项为正数时,应分解为两同号因数,它们的符号与一次项系数的符号相同;常数项为负数时,应将它分解为两异号因数,使十字连线上两数之积绝对值较大的一组与一次项系数的符号相同.【类题·通】
十字相乘法因式分解的形式
尝试把某些二次三项式如ax2+bx+c分解因式,先把a分解成a=a1a2,把c分解成c=c1c2,并且排列如下:这里按斜线交叉相乘的积的和就是a1c2+a2c1,如果它正好等于二次三项式ax2+bx+c中一次项的系数b,那么ax2+bx+c就可以分解成(a1x+c1)(a2x+c2),其中a1,c1是上图中上面一行的两个数,a2,c2是下面一行的两个数.【习练·破】
1.x2+10x+16分解因式为 ( )
A.(x+2)(x+8) B.(x-2)(x+8)
C.(x+2)(x-8) D.(x-2)(x-8)【解析】选A.x2+10x+16=(x+2)(x+8).
1×8+1×2=102.x2-13xy-30y2分解因式为 ( )
A.(x-3y)(x-10y) B.(x+15y)(x-2y)
C.(x+10y)(x+3y) D.(x-15y)(x+2y)【解析】选D.x2-13xy-30y2=(x-15y)(x+2y)
1×2y+1×(-15y)=-13y3.6x2-29x+35分解因式为 ( )
A.(2x-7)(3x-5) B.(3x-7)(2x-5)
C.(3x-7)(2x+5) D.(2x-7)(3x+5)【解析】选B.6x2-29x+35=(3x-7)(2x-5)
3×(-5)+2×(-7)=-29【加练·固】
1.因式分解(x2-7x)2+10(x2-7x)-24.
【解析】(x2-7x)2+10(x2-7x)-24=(x2-7x+12)(x2-7x-2)
=(x-3)(x-4)(x2-7x-2).2.已知a2-ab-6b2=0(a≠0,b≠0),求 的值.【解析】因为a2-ab-6b2=0,所以(a-3b)(a+2b)=0,
所以a=3b或a=-2b,
当a=3b时,
当a=-2b时,
=-2 .类型三 方程的解集
角度1 一元一次方程的解集
【典例】(多选题)下列方程中,解集为{-3}的方程
是 ( )
A. x+1=0 B.2x+1=-8-x
C.3-3x=1 D.2x+6=0【思维·引】
解一元一次方程时,通过移项、合并同类项、系数化为1等过程,解方程.
【解析】选ABD.把x=-3分别代入各选项,只有C选项左右两边的值不相等.角度2 一元二次方程的解集
【典例】求下列方程的解集:
(1)x(x-2)+x-2=0.
(2)x2+5x-6=0.【思维·引】
(1)提取公因式x-2把原方程化为两个因式的积的形式,解方程.
(2)对于二次三项式,一般先采用十字相乘法分解因式,分解因式后再解方程即可.【解析】(1)因式分解,得:(x-2)(x+1)=0.
于是得x-2=0或x+1=0,即x=2或x=-1,因此方程的解集为{-1,2}.(2)分解因式得:x2+5x-6=(x-1)(x+6),1×(-1)+1×6=5因为x2+5x-6=0,
所以(x-1)(x+6)=0,
所以x-1=0或x+6=0,
即x=1或x=-6.
因此方程的解集为{-6,1}. 【类题·通】
利用因式分解法解一元二次方程的步骤:
①将方程的右边化为0;
②将方程的左边进行因式分解;
③令每个因式为0,得到两个一元一次方程;
④解一元一次方程,得到方程的解.【发散·拓】对于二次三项式,采用十字相乘法分解因式时,要注意把二次项系数和常数项分解,交叉相乘,两个因式的和正好等于一次项系数.注意,交叉相乘横着写.【习练·破】
求下列方程的解集:
(1)5x2-2x- =x2-2x+ .
(2)12x2+5x-2=0.【解析】(1)移项、合并同类项,得4x2-1=0.
因式分解,得(2x+1)(2x-1)=0.
于是得2x+1=0或2x-1=0,即x=- 或x= ,
因此方程的解集为 (2)分解因式得:
12x2+5x-2=(3x+2)(4x-1)3×(-1)+4×2=5因为12x2+5x-2=0,
所以(3x+2)(4x-1)=0,
所以3x+2=0或4x-1=0,
即x=- 或x= ,因此方程的解集为 角度3 分类讨论思想的应用
【典例】解方程ax2-(a+1)x+1=0.
【思维·引】把二次项系数分为a=0和a≠0两种情况讨论,第一种情况是解一元一次方程,第二种情况是解一元二次方程.【解析】当a=0时,原方程可化为-x+1=0,
所以x=1,当a≠0时,对于ax2-(a+1)x+1来说,因为a×1=a,
(-1)×(-1)=1,a×(-1)+1×(-1)=-(a+1).如图所示
ax2-(a+1)x+1=(ax-1)(x-1),所以原方程可化为
(ax-1)(x-1)=0,
所以ax-1=0或x-1=0,
所以x= 或x=1.【类题·通】
形如ax2+bx+c=0(含参)的方程的解法
方程的二次项系数中含有参数时,要讨论二次项系数是否可以等于零,当二次项系数等于零时,讨论方程变为一元一次方程或其他情况,当二次项系数不为0时,解一元二次方程.【习练·破】
解方程12x2-ax-a2=0.【解析】当a=0时,原方程可化为:
12x2=0,所以x=0,当a≠0时,因为3×4=12,-a×a
=-a2,3×a+4×(-a)=3a-4a=-a,如图所示所以12x2-ax-a2=(3x-a)(4x+a),
所以原方程可化为(3x-a)(4x+a)=0.
所以3x-a=0或4x+a=0,
所以x1= ,x2=- .
