2020版新教材高中数学第三章函数3.1.1.1函数的概念课件新人教B版必修1:55张PPT
文档属性
| 名称 | 2020版新教材高中数学第三章函数3.1.1.1函数的概念课件新人教B版必修1:55张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览



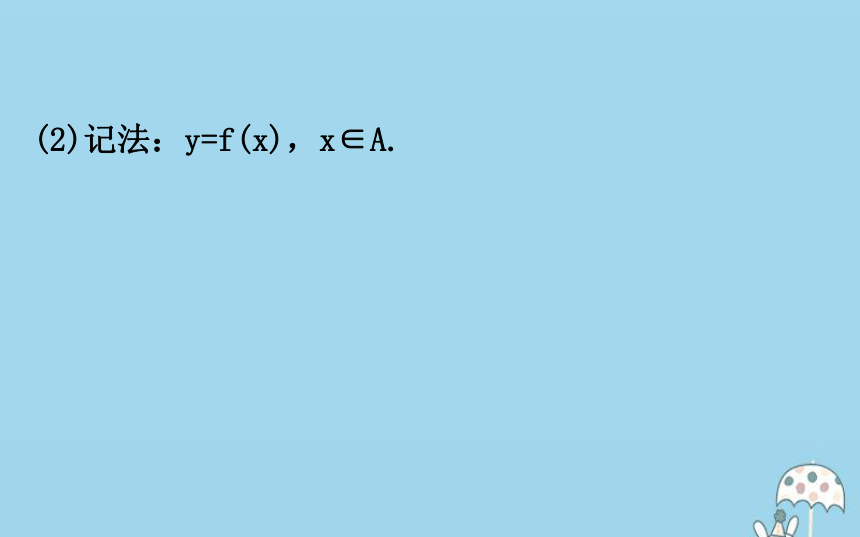








文档简介
课件55张PPT。第三章 函 数
3.1 函数的概念与性质
3.1.1 函数及其表示方法
第1课时 函数的概念函数的概念
(1)定义:给定两个非空数集A与B,以及对应关系f,如果对于集合A中的每一个实数x,在集合B中都有唯一确定的实数y与x对应,则称f为定义在集合A上的一个函数.(2)记法:y=f(x),x∈A.(3)定义:【思考】
(1)对应关系还可以用哪些字母表示?
提示:对应关系还可以用小写英文字母如g,h等表示.(2)函数的值域与集合B是什么关系?
提示:函数的值域{y∈B|y=f(x),x∈A}?B.(3)y=f(x)表示的是“y等于f与x的乘积”吗?
提示:符号y=f(x)是“y是x的函数”的数学表示,应理解为x是自变量,它是关系所施加的对象.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)任何两个集合都可以建立函数关系. ( )
(2)集合A中的两个实数x可以对应集合B中的一个实数y.
( )
(3)函数的值域即为集合B. ( )提示:(1)×.集合A,B应为非空数集.
(2)√.符合函数的定义.
(3)×.值域是集合B的子集.2.若函数定义在集合A={-1,0,1}上,f为“乘2”,则函数的值域B=________.?
【解析】B={-2,0,2}.
答案:{-2,0,2}3.用区间表示函数f(x)= 的定义域是________.?
【解析】由题意得x-1>0,所以x>1,
定义域为(1,+∞).
答案:(1,+∞)类型一 函数关系的判断
【典例】1.(2019·泰安高一检测)下列四个图像中,不可能是函数图像的是 ( )2.在下列从集合A到集合B的对应关系中,能确定y是x的函数的是 ( )
①A={x|x∈Z},B={y|y∈Z},f为“除以3”;
②A={x|x>0,x∈R},B={y|y∈R},f为“求3x的平方根”;③A=R,B=R,f为“求平方”;
④A={x|-1≤x≤1,x∈R},B={0},f为“乘以0”.
A.①④ B.②③④
C.②③ D.③④【思维·引】
1.作与x轴垂直的直线,此直线与函数的图像至多有一个公共点.
2.先看集合A、B是否为非空数集,再判断非空数集A中任取一个数,在非空数集B中是否有唯一的数与之对应,若不是,则不是函数.【解析】1.选B.根据题意,对于选项A,对于任意的x ,有唯一确定的y与其对应,故成立,对于B,由于一个x,可有两个y对应,不成立,对于C,由于满足对于任意的x ,有唯一确定的y与其对应,因此是函数图像,对于D,也是作一条垂直于x轴的直线,交点至多一个即可.2.选D.①在对应关系f下,A中不能被3整除的数在B中没有唯一确定的数与它对应,所以不能确定y是x的函数;②在对应关系f下,A中的数在B中有两个数与之对应,所以不能确定y是x的函数;③④符合函数的定义.【内化·悟】
理解函数的概念,需要把握哪几个要点?提示:(1)集合A,B是非空数集;(2)强调“三性”:任意性、存在性、唯一性,即对于非空数集A中的任意一个(任意性)元素x,在非空数集B中都有(存在性)唯一(唯一性)的元素y与之对应.这三性只要有一个不满足,便不能构成函数.【类题·通】
1.判断一个对应是否是函数的方法2.根据图形判断对应是否为函数的步骤
(1)任取一条垂直于x轴的直线l.
(2)在定义域内平行移动直线l.
(3)若l与图形有且只有一个交点,则是函数;若在定义域内没有交点或有两个或两个以上的交点,则不是函数.如图所示:【习练·破】
已知集合A={1,2,3,4},B={5,6,7},在下列A到B的四种对应关系中,存在函数关系的个数是 ( )A. 1 B. 2 C. 3 D. 4【解析】选B.根据函数的定义可知,集合A中每一个实数在B中都有唯一确定的实数与之对应,其中①③均满足函数的定义.【加练·固】
如图可作为函数y=f(x)的图像的是 ( )【解析】选D.观察图像可知,A,B,C中任取一个x的值,y有可能有多个值与之对应,所以不是函数图像.D中图像是函数图像.类型二 求函数的定义域
【典例】1.函数y= 的定义域为 ( )
A.(-∞,-5)∪(-5,5)∪(5,+∞)
B.[4,+∞)
C.(4,5)
D.[4,5)∪(5,+∞)2.设全集为R,函数f(x)= 的定义域为M,则?RM
=世纪金榜导学号( )
A.{x|x≥2或x=-1}
B.{x|x<2且x≠-1}
C.{x|x≥2}
D.{x|x>2或x=-1}【思维·引】1.根据被开方数大于等于0,分母不等于0求范围.
2.根据被开方数大于等于0,分母不等于0,0次幂的底数不等于0求范围.【解析】1.选D.因为函数有意义当且仅当
解得4≤x<5或x>5,
故函数y= 的定义域为[4,5)∪(5,+∞).2.选A.因为函数有意义当且仅当
解得x<2且x≠-1,
所以M={x|x<2且x≠-1},
所以?RM={x|x≥2或x=-1}.【内化·悟】
求函数的定义域时需要关注哪些方面?
提示:关注解析式中是否含有分式、根号、零次幂.【类题·通】
已知函数的解析式,求函数的定义域
(1)本质:求使得函数解析式有意义的自变量的取值范围.(2)常见题型
①如果f(x)是整式,那么函数的定义域是实数集R.
②如果f(x)是分式,那么函数的定义域是使分母不等于零的实数的集合.
③如果f(x)是二次根式,那么函数的定义域是使根号内的式子大于或等于零的实数的集合.④y=x0要求x≠0.
⑤如果f(x)是由几个部分的数学式子构成的,那么函数定义域是使各部分式子都有意义的实数集合(即求各部分定义域的交集).【习练·破】
1.函数f(x)= 的定义域为 ( )
A.[-3,-1)∪(-1,+∞)
B.(-3,-1)∪(-1,+∞)
C.[-1,+∞)
D.[-3,+∞)【解析】选A.因为函数有意义当且仅当
解得x≥-3,且x≠-1,
所以f(x)的定义域为:[-3,-1)∪(-1,+∞).2.函数y= 的定义域为________.?【解析】令-x2+2x+3≥0,
即x2-2x-3≤0,
解得-1≤x≤3,
所以函数的定义为[-1,3].
答案:[-1,3]【加练·固】
函数y= 的定义域为 ( )【解析】选B.由题意得:2x+1≥0,
解得x≥
故函数的定义域是 类型三 函数对应关系的应用
角度1 对应关系的选取
【典例】已知A={x|0≤x≤9},B={y|0≤x≤3},下列
对应关系不表示定义在A上的函数的是 ( )
A.f为“乘 ” B.f为“乘 ”
C.f为“乘 ” D.f为“求算术平方根”【思维·引】根据函数的定义判断.
【解析】选A.对于对应f:“乘 ”,x=9∈A时,
y=4.5?B,所以此对应关系不是定义在集合A上的函
数,B,C,D均是定义在集合A上的函数.【素养·探】
在判断函数关系时,常常用到核心素养中的逻辑推理,根据函数的定义判断对应关系是否构成函数关系.
本例中,若f为“求平方根”,则f是否是定义在集合A上的函数?【解析】因为任何一个正数都有两个平方根,故集合A中的任何一个正数都对应两个实数,不符合函数的定义,故f不是定义在集合A上的函数.角度2 利用对应关系求值
【典例】已知f为“平方加1”是定义在集合A上的函数,那么值域中的元素5在集合A中对应的元素是
( )
世纪金榜导学号
A.26 B.2 C.-2 D.±2【思维·引】设对应的元素为x,列方程求值.【解析】选D.因为f为“平方加1”,设集合A中对应的元素为x,由5=x2+1,得x=±2,
所以值域中元素5在A中对应的元素为±2.【类题·通】
1.关于对应关系的选择
根本的方法是依据函数的定义进行判断,判断时可以借助区间的端点值、区间中的特殊值进行验证、排除,另外值域一定是集合B的子集.2.关于利用对应关系求值
利用对应关系建立定义域A中的x与值域中的y之间的方程,通过解方程求值,其中x可以是一个或多个,而y值只能是一个.【习练·破】
已知A=B=R,x∈A,y∈B,对应关系f为“乘以a加b”是定义在集合A上的函数,若集合A中的3和10分别对应集合B中的1和8,则5对应的元素是 ( )
A.3 B.4 C.5 D.6【解析】选A.A=B=R,x∈A,y∈B,f为“乘以a加
b”,所以有 解得:
即f为“乘以1减2”,5在f下的函数值f(5)=1×5-2=3.
3.1 函数的概念与性质
3.1.1 函数及其表示方法
第1课时 函数的概念函数的概念
(1)定义:给定两个非空数集A与B,以及对应关系f,如果对于集合A中的每一个实数x,在集合B中都有唯一确定的实数y与x对应,则称f为定义在集合A上的一个函数.(2)记法:y=f(x),x∈A.(3)定义:【思考】
(1)对应关系还可以用哪些字母表示?
提示:对应关系还可以用小写英文字母如g,h等表示.(2)函数的值域与集合B是什么关系?
提示:函数的值域{y∈B|y=f(x),x∈A}?B.(3)y=f(x)表示的是“y等于f与x的乘积”吗?
提示:符号y=f(x)是“y是x的函数”的数学表示,应理解为x是自变量,它是关系所施加的对象.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)任何两个集合都可以建立函数关系. ( )
(2)集合A中的两个实数x可以对应集合B中的一个实数y.
( )
(3)函数的值域即为集合B. ( )提示:(1)×.集合A,B应为非空数集.
(2)√.符合函数的定义.
(3)×.值域是集合B的子集.2.若函数定义在集合A={-1,0,1}上,f为“乘2”,则函数的值域B=________.?
【解析】B={-2,0,2}.
答案:{-2,0,2}3.用区间表示函数f(x)= 的定义域是________.?
【解析】由题意得x-1>0,所以x>1,
定义域为(1,+∞).
答案:(1,+∞)类型一 函数关系的判断
【典例】1.(2019·泰安高一检测)下列四个图像中,不可能是函数图像的是 ( )2.在下列从集合A到集合B的对应关系中,能确定y是x的函数的是 ( )
①A={x|x∈Z},B={y|y∈Z},f为“除以3”;
②A={x|x>0,x∈R},B={y|y∈R},f为“求3x的平方根”;③A=R,B=R,f为“求平方”;
④A={x|-1≤x≤1,x∈R},B={0},f为“乘以0”.
A.①④ B.②③④
C.②③ D.③④【思维·引】
1.作与x轴垂直的直线,此直线与函数的图像至多有一个公共点.
2.先看集合A、B是否为非空数集,再判断非空数集A中任取一个数,在非空数集B中是否有唯一的数与之对应,若不是,则不是函数.【解析】1.选B.根据题意,对于选项A,对于任意的x ,有唯一确定的y与其对应,故成立,对于B,由于一个x,可有两个y对应,不成立,对于C,由于满足对于任意的x ,有唯一确定的y与其对应,因此是函数图像,对于D,也是作一条垂直于x轴的直线,交点至多一个即可.2.选D.①在对应关系f下,A中不能被3整除的数在B中没有唯一确定的数与它对应,所以不能确定y是x的函数;②在对应关系f下,A中的数在B中有两个数与之对应,所以不能确定y是x的函数;③④符合函数的定义.【内化·悟】
理解函数的概念,需要把握哪几个要点?提示:(1)集合A,B是非空数集;(2)强调“三性”:任意性、存在性、唯一性,即对于非空数集A中的任意一个(任意性)元素x,在非空数集B中都有(存在性)唯一(唯一性)的元素y与之对应.这三性只要有一个不满足,便不能构成函数.【类题·通】
1.判断一个对应是否是函数的方法2.根据图形判断对应是否为函数的步骤
(1)任取一条垂直于x轴的直线l.
(2)在定义域内平行移动直线l.
(3)若l与图形有且只有一个交点,则是函数;若在定义域内没有交点或有两个或两个以上的交点,则不是函数.如图所示:【习练·破】
已知集合A={1,2,3,4},B={5,6,7},在下列A到B的四种对应关系中,存在函数关系的个数是 ( )A. 1 B. 2 C. 3 D. 4【解析】选B.根据函数的定义可知,集合A中每一个实数在B中都有唯一确定的实数与之对应,其中①③均满足函数的定义.【加练·固】
如图可作为函数y=f(x)的图像的是 ( )【解析】选D.观察图像可知,A,B,C中任取一个x的值,y有可能有多个值与之对应,所以不是函数图像.D中图像是函数图像.类型二 求函数的定义域
【典例】1.函数y= 的定义域为 ( )
A.(-∞,-5)∪(-5,5)∪(5,+∞)
B.[4,+∞)
C.(4,5)
D.[4,5)∪(5,+∞)2.设全集为R,函数f(x)= 的定义域为M,则?RM
=世纪金榜导学号( )
A.{x|x≥2或x=-1}
B.{x|x<2且x≠-1}
C.{x|x≥2}
D.{x|x>2或x=-1}【思维·引】1.根据被开方数大于等于0,分母不等于0求范围.
2.根据被开方数大于等于0,分母不等于0,0次幂的底数不等于0求范围.【解析】1.选D.因为函数有意义当且仅当
解得4≤x<5或x>5,
故函数y= 的定义域为[4,5)∪(5,+∞).2.选A.因为函数有意义当且仅当
解得x<2且x≠-1,
所以M={x|x<2且x≠-1},
所以?RM={x|x≥2或x=-1}.【内化·悟】
求函数的定义域时需要关注哪些方面?
提示:关注解析式中是否含有分式、根号、零次幂.【类题·通】
已知函数的解析式,求函数的定义域
(1)本质:求使得函数解析式有意义的自变量的取值范围.(2)常见题型
①如果f(x)是整式,那么函数的定义域是实数集R.
②如果f(x)是分式,那么函数的定义域是使分母不等于零的实数的集合.
③如果f(x)是二次根式,那么函数的定义域是使根号内的式子大于或等于零的实数的集合.④y=x0要求x≠0.
⑤如果f(x)是由几个部分的数学式子构成的,那么函数定义域是使各部分式子都有意义的实数集合(即求各部分定义域的交集).【习练·破】
1.函数f(x)= 的定义域为 ( )
A.[-3,-1)∪(-1,+∞)
B.(-3,-1)∪(-1,+∞)
C.[-1,+∞)
D.[-3,+∞)【解析】选A.因为函数有意义当且仅当
解得x≥-3,且x≠-1,
所以f(x)的定义域为:[-3,-1)∪(-1,+∞).2.函数y= 的定义域为________.?【解析】令-x2+2x+3≥0,
即x2-2x-3≤0,
解得-1≤x≤3,
所以函数的定义为[-1,3].
答案:[-1,3]【加练·固】
函数y= 的定义域为 ( )【解析】选B.由题意得:2x+1≥0,
解得x≥
故函数的定义域是 类型三 函数对应关系的应用
角度1 对应关系的选取
【典例】已知A={x|0≤x≤9},B={y|0≤x≤3},下列
对应关系不表示定义在A上的函数的是 ( )
A.f为“乘 ” B.f为“乘 ”
C.f为“乘 ” D.f为“求算术平方根”【思维·引】根据函数的定义判断.
【解析】选A.对于对应f:“乘 ”,x=9∈A时,
y=4.5?B,所以此对应关系不是定义在集合A上的函
数,B,C,D均是定义在集合A上的函数.【素养·探】
在判断函数关系时,常常用到核心素养中的逻辑推理,根据函数的定义判断对应关系是否构成函数关系.
本例中,若f为“求平方根”,则f是否是定义在集合A上的函数?【解析】因为任何一个正数都有两个平方根,故集合A中的任何一个正数都对应两个实数,不符合函数的定义,故f不是定义在集合A上的函数.角度2 利用对应关系求值
【典例】已知f为“平方加1”是定义在集合A上的函数,那么值域中的元素5在集合A中对应的元素是
( )
世纪金榜导学号
A.26 B.2 C.-2 D.±2【思维·引】设对应的元素为x,列方程求值.【解析】选D.因为f为“平方加1”,设集合A中对应的元素为x,由5=x2+1,得x=±2,
所以值域中元素5在A中对应的元素为±2.【类题·通】
1.关于对应关系的选择
根本的方法是依据函数的定义进行判断,判断时可以借助区间的端点值、区间中的特殊值进行验证、排除,另外值域一定是集合B的子集.2.关于利用对应关系求值
利用对应关系建立定义域A中的x与值域中的y之间的方程,通过解方程求值,其中x可以是一个或多个,而y值只能是一个.【习练·破】
已知A=B=R,x∈A,y∈B,对应关系f为“乘以a加b”是定义在集合A上的函数,若集合A中的3和10分别对应集合B中的1和8,则5对应的元素是 ( )
A.3 B.4 C.5 D.6【解析】选A.A=B=R,x∈A,y∈B,f为“乘以a加
b”,所以有 解得:
即f为“乘以1减2”,5在f下的函数值f(5)=1×5-2=3.
