2020版新教材高中数学第三章函数3.1.1.2函数概念的综合应用课件新人教B版必修1:69张PPT
文档属性
| 名称 | 2020版新教材高中数学第三章函数3.1.1.2函数概念的综合应用课件新人教B版必修1:69张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 23:03:32 | ||
图片预览











文档简介
课件69张PPT。第2课时
函数概念的综合应用1.同一个函数【思考】
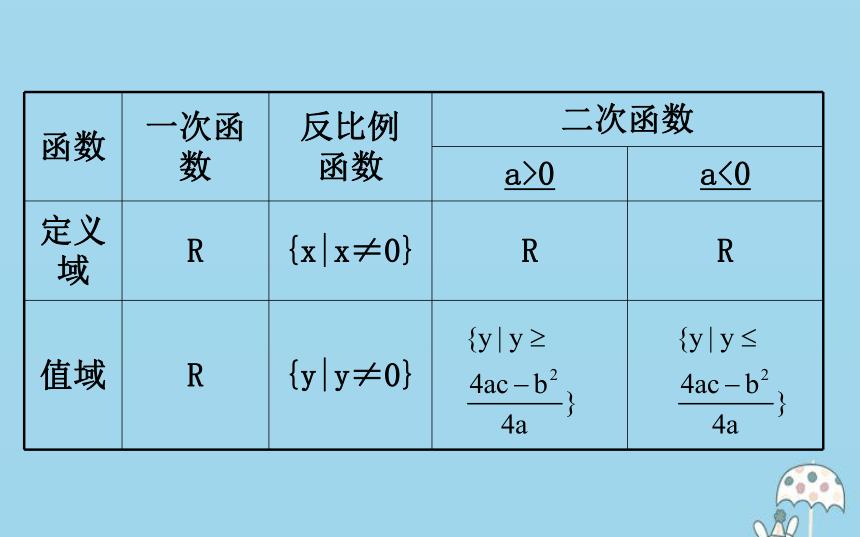
函数有定义域、对应关系和值域三要素,为什么判断两个函数是否是同一个函数,只看定义域和对应关系?提示:由函数的定义域和对应关系可以求出函数的值域,所以判断两个函数是否是同一个函数,只看定义域和对应关系即可.2.常见函数的定义域和值域【思考】
求二次函数y=ax2+bx+c(a≠0)的值域时为什么分a>0和a<0两种情况?提示:当a>0时,二次函数的图像是开口向上的抛物
线,观察图像得值域为
当a<0时,二次函数的图像是开口向下的抛物线,观察
图像得值域为 【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)若两个函数的定义域与值域都相同,则这两个函数是同一个函数. ( )(2)函数f(x)=x2-x与g(t)=t2-t不是同一个函数.
( )
(3)函数f(x)= +1的值域是(-∞,1)∪(1,+∞).
( )提示:(1)×.例如f(x)= 与g(x)= 的定义域与值
域相同,但这两个函数不是同一个函数.
(2)×.函数f(x)=x2-x与g(t)=t2-t的定义域都是R,对
应关系完全一致,所以这两个函数是同一个函数.
(3)√.因为 ≠0,所以 +1≠1.2.若函数y=x2-3x的定义域为{-1,0,2,3},则其值
域为 ( )
A.{-2,0,4} B.{-2,0,2,4}
C. D.[0,3]【解析】选A.依题意,当x=-1时,y=4;
当x=0时,y=0;
当x=2时,y=-2;
当x=3时,y=0.
所以函数y=x2-3x的值域为{-2,0,4}.3.设函数f(x)=2x+3的值域是[-1,5],则其定义域为_______.?
【解析】由-1≤2x+3≤5,解得-2≤x≤1,即函数定义域为[-2,1].
答案:[-2,1]类型一 判断两个函数是否是同一个函数
【典例】1.若函数f(x)=( )2与g(x)=x(x∈D)是同一
个函数,则D可以是 ( )
A.(-∞,0) B.(0,+∞)
C.[0,+∞) D.(-∞,0]2.判断下列各组中的两个函数是同一个函数的为
( )
世纪金榜导学号
(1)y1= y2=x-5.
(2)y1= (3)f(x)=x,g(x)=
(4)f(x)= F(x)=
A.(1)、(2) B.(2)、(3)
C.(4) D.(3)【思维·引】
1.根据相等函数的定义域相同求D.
2.先求定义域,若定义域不同,则不相等;若定义域相同,再化简函数的解析式,看对应关系是否相同.【解析】1.选C.函数f(x)的定义域为[0,+∞),
即D=[0,+∞).2.选C.对于(1),两个函数的定义域不同,所以不是同
一个函数;对于(2),两个函数的定义域不同,如当
x=-1时函数y1= 无意义,但y2=
有意义,所以不是同一个函数;对于(3),g(x)=
=|x|,两个函数的对应关系不同,所以不是同一个函
数;对于(4),f(x)= 所以两个
函数定义域相同,对应关系相同,是同一个函数.【内化·悟】
判断两个函数是否是同一个函数的步骤是什么?
提示:先分别求出两个函数的定义域,若定义域相同则考查解析式是否相同.【类题·通】
判断函数是同一函数的三个步骤和两个注意点
(1)判断函数是否是同一函数的三个步骤.(2)两个注意点.
①在化简解析式时,必须是等价变形;
②与用哪个字母表示解析式无关.【习练·破】
下列各组函数中表示同一个函数的是 ( )
A.y= 与y=x+3
B.y= 与y=x-1C.y=x0(x≠0)与y=1(x≠0)
D.y=2x+1,x∈Z与y=2x-1,x∈Z
【解析】选C.选项A中两函数的定义域不同;选项B,D中两函数的对应关系不同.【加练·固】
判断下列各组函数是否是同一个函数,并说明理由.
(1)f(x)=2x+1(x∈R),g(x)=2x+1(x∈N*).
(2)f(x)=x2,g(x)=
(3)y= y=x-1.【解析】(1)对应关系一致,但定义域不同,因而不是同一个函数.
(2)定义域相同,但对应关系不一致,因而不是同一个函数.(3)y= =|x-1|,与函数y=x-1的对应关系不
一致,所以两个函数不是同一个函数.类型二 利用函数的解析式求值(式)
【典例】已知f(x)= g(x)=x2+2.
(1)求f(2),g(2),f(g(2));(2)求f(g(x)).【思维·引】
(1)将x分别替换成2求出f(2),g(2),再求f(g(2)).
(2)将x替换成 代入化简.【解析】(1)f(2)= g(2)=22+2=6,
把g(2)=22+2=6代入f(x)=
得f(g(2))=f(6)=
(2)f(g(x))=f(x2+2)= 【内化·悟】
函数f(x)中的x只能是数字吗?
提示:可以是数字,也可以是字母、式子.【类题·通】
利用函数的解析式求值
函数解析式中的x可以是数字、字母、式子,只要将数字、字母、式子整体代入,即可化简求值,代入遵循从里向外的代入顺序.【习练·破】
设f(x)= 其中x≠0,且x≠1.则f(f(x))=______.?【解析】由f(x)= 则f(f(x))=
答案: 【加练·固】
设函数f(x)=3x2-1,则f(a)-f(-a)的值是 ( )
A. 0 B. 3a2-1 C. 6a2-2 D. 6a2【解析】选A.f(a)-f(-a)
=3a2-1-[3(-a)2-1]=0.类型三 求函数的值域
角度1 利用不等式的性质求值域
【典例】1.已知函数f(x)= 则f(x)的值域是( )2.求函数f(x)= 的值域. 世纪金榜导学号【思维·引】
1.利用不等式的性质推导 的范围或变形后利用
方程有解求值域.
2.对解析式变形后利用不等式的性质求值域.【解析】1.选C.方法一:因为x2+2≥2,所以
所以f(x)的值域为 方法二:设t是所求值域中的元素,则关于x的方程
应该有解,即x2= -2应该有解,所以 -2≥0,
即 解得0因为f(x)= 因为x≠1,所以 ≠0,所以f(x)≠5,
所以函数f(x)= 的值域为(-∞,5)∪(5,+∞).【素养·探】
利用不等式求值域时,常常用到核心素养中的数学运
算,利用解析式的变形,推导解析式的范围.
将本例2中的函数变为f(x)= 试求值域.【解析】f(x)= 的定义域为
因为f(x)=
所以f(x)≠ 所以函数的值域为 角度2 配方法求值域
【典例】求下列函数的值域 世纪金榜导学号
(1)f(x)=x2-2x+2.(2) f(x)= 【思维·引】
(1)先配方再求值域.
(2)先换元,再配方求值域.【解析】(1)函数的定义域为R,
因为f(x)=x2-2x+2=(x-1)2+1≥1,
所以函数的值域为[1,+∞).(2)因为函数有意义当且仅当x+1≥0,
即x≥-1,
故函数的定义域是[-1,+∞).
设t= 则x=t2-1(t≥0),于是g(t)=
又因为t≥0,故g(t)≥
所以函数的值域是 【类题·通】
求函数值域的常用方法
(1)利用不等式的性质:结合定义域,利用x的变形,推导解析式的范围.
(2)利用方程有解:设值域内的元素t,用t表示x,根据x的范围求t的范围,即值域.(3)配方法:是求“二次函数”类值域的基本方法.
(4)换元法:运用新元代换,将所给函数化成值域易确
定的函数,从而求得原函数的值域.对于f(x)=ax+b+
(其中a,b,c,d为常数,且ac≠0)型的函数常
用换元法.(5)分离常数法:此方法主要是针对分子分母同次的分式,即将分式转化为“反比例函数类”的形式,便于求值域.【发散·拓】
对于形如y= 的函数,还可以把已知函
数转化为关于变量的二次方程,再利用方程有解,即
判别式非负.从而求得原函数值域的方法叫判别式法.【延伸·练】
试用此法求函数y= 的值域.【解析】易知函数的定义域是R,
由y= 得yx2-x+y=0,
当y=0时,x=0,所以y可以为0;当y≠0时,Δ=1-4y2≥0,
所以
综上可得,所求函数的值域为 【习练·破】
(2019·天津高一检测)求下列函数的值域.
(1)f(x)= (2)y= 【解析】(1)f(x)= 的定义域为R,
x2+x+1=
所以
所以f(x)= 的值域为 (2)令t= (t≥0),则x=1-t2,换元可得函数的解
析式:g(t)=1-t2+4t
=-(t-2)2+5,又因为t≥0,故g(t)≤5,.
所以函数的值域是(-∞,5].【加练·固】
求下列函数的值域.
(1)y=
(2)y=
(3)y=3x2-x+2.【解析】(1)方法一:由x2≥0及4-x2≥0,
观察得 ∈[0,2],
故此函数的值域为[0,2].方法二:由 x2≥0得-x2≤0,得4-x2≤4,
所以0≤ ≤2,
故此函数的值域为[0,2].(2)y=
因为 所以y≠
所以函数的值域为 (3)函数y=
值域为
函数概念的综合应用1.同一个函数【思考】
函数有定义域、对应关系和值域三要素,为什么判断两个函数是否是同一个函数,只看定义域和对应关系?提示:由函数的定义域和对应关系可以求出函数的值域,所以判断两个函数是否是同一个函数,只看定义域和对应关系即可.2.常见函数的定义域和值域【思考】
求二次函数y=ax2+bx+c(a≠0)的值域时为什么分a>0和a<0两种情况?提示:当a>0时,二次函数的图像是开口向上的抛物
线,观察图像得值域为
当a<0时,二次函数的图像是开口向下的抛物线,观察
图像得值域为 【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)若两个函数的定义域与值域都相同,则这两个函数是同一个函数. ( )(2)函数f(x)=x2-x与g(t)=t2-t不是同一个函数.
( )
(3)函数f(x)= +1的值域是(-∞,1)∪(1,+∞).
( )提示:(1)×.例如f(x)= 与g(x)= 的定义域与值
域相同,但这两个函数不是同一个函数.
(2)×.函数f(x)=x2-x与g(t)=t2-t的定义域都是R,对
应关系完全一致,所以这两个函数是同一个函数.
(3)√.因为 ≠0,所以 +1≠1.2.若函数y=x2-3x的定义域为{-1,0,2,3},则其值
域为 ( )
A.{-2,0,4} B.{-2,0,2,4}
C. D.[0,3]【解析】选A.依题意,当x=-1时,y=4;
当x=0时,y=0;
当x=2时,y=-2;
当x=3时,y=0.
所以函数y=x2-3x的值域为{-2,0,4}.3.设函数f(x)=2x+3的值域是[-1,5],则其定义域为_______.?
【解析】由-1≤2x+3≤5,解得-2≤x≤1,即函数定义域为[-2,1].
答案:[-2,1]类型一 判断两个函数是否是同一个函数
【典例】1.若函数f(x)=( )2与g(x)=x(x∈D)是同一
个函数,则D可以是 ( )
A.(-∞,0) B.(0,+∞)
C.[0,+∞) D.(-∞,0]2.判断下列各组中的两个函数是同一个函数的为
( )
世纪金榜导学号
(1)y1= y2=x-5.
(2)y1= (3)f(x)=x,g(x)=
(4)f(x)= F(x)=
A.(1)、(2) B.(2)、(3)
C.(4) D.(3)【思维·引】
1.根据相等函数的定义域相同求D.
2.先求定义域,若定义域不同,则不相等;若定义域相同,再化简函数的解析式,看对应关系是否相同.【解析】1.选C.函数f(x)的定义域为[0,+∞),
即D=[0,+∞).2.选C.对于(1),两个函数的定义域不同,所以不是同
一个函数;对于(2),两个函数的定义域不同,如当
x=-1时函数y1= 无意义,但y2=
有意义,所以不是同一个函数;对于(3),g(x)=
=|x|,两个函数的对应关系不同,所以不是同一个函
数;对于(4),f(x)= 所以两个
函数定义域相同,对应关系相同,是同一个函数.【内化·悟】
判断两个函数是否是同一个函数的步骤是什么?
提示:先分别求出两个函数的定义域,若定义域相同则考查解析式是否相同.【类题·通】
判断函数是同一函数的三个步骤和两个注意点
(1)判断函数是否是同一函数的三个步骤.(2)两个注意点.
①在化简解析式时,必须是等价变形;
②与用哪个字母表示解析式无关.【习练·破】
下列各组函数中表示同一个函数的是 ( )
A.y= 与y=x+3
B.y= 与y=x-1C.y=x0(x≠0)与y=1(x≠0)
D.y=2x+1,x∈Z与y=2x-1,x∈Z
【解析】选C.选项A中两函数的定义域不同;选项B,D中两函数的对应关系不同.【加练·固】
判断下列各组函数是否是同一个函数,并说明理由.
(1)f(x)=2x+1(x∈R),g(x)=2x+1(x∈N*).
(2)f(x)=x2,g(x)=
(3)y= y=x-1.【解析】(1)对应关系一致,但定义域不同,因而不是同一个函数.
(2)定义域相同,但对应关系不一致,因而不是同一个函数.(3)y= =|x-1|,与函数y=x-1的对应关系不
一致,所以两个函数不是同一个函数.类型二 利用函数的解析式求值(式)
【典例】已知f(x)= g(x)=x2+2.
(1)求f(2),g(2),f(g(2));(2)求f(g(x)).【思维·引】
(1)将x分别替换成2求出f(2),g(2),再求f(g(2)).
(2)将x替换成 代入化简.【解析】(1)f(2)= g(2)=22+2=6,
把g(2)=22+2=6代入f(x)=
得f(g(2))=f(6)=
(2)f(g(x))=f(x2+2)= 【内化·悟】
函数f(x)中的x只能是数字吗?
提示:可以是数字,也可以是字母、式子.【类题·通】
利用函数的解析式求值
函数解析式中的x可以是数字、字母、式子,只要将数字、字母、式子整体代入,即可化简求值,代入遵循从里向外的代入顺序.【习练·破】
设f(x)= 其中x≠0,且x≠1.则f(f(x))=______.?【解析】由f(x)= 则f(f(x))=
答案: 【加练·固】
设函数f(x)=3x2-1,则f(a)-f(-a)的值是 ( )
A. 0 B. 3a2-1 C. 6a2-2 D. 6a2【解析】选A.f(a)-f(-a)
=3a2-1-[3(-a)2-1]=0.类型三 求函数的值域
角度1 利用不等式的性质求值域
【典例】1.已知函数f(x)= 则f(x)的值域是( )2.求函数f(x)= 的值域. 世纪金榜导学号【思维·引】
1.利用不等式的性质推导 的范围或变形后利用
方程有解求值域.
2.对解析式变形后利用不等式的性质求值域.【解析】1.选C.方法一:因为x2+2≥2,所以
所以f(x)的值域为 方法二:设t是所求值域中的元素,则关于x的方程
应该有解,即x2= -2应该有解,所以 -2≥0,
即 解得0
所以函数f(x)= 的值域为(-∞,5)∪(5,+∞).【素养·探】
利用不等式求值域时,常常用到核心素养中的数学运
算,利用解析式的变形,推导解析式的范围.
将本例2中的函数变为f(x)= 试求值域.【解析】f(x)= 的定义域为
因为f(x)=
所以f(x)≠ 所以函数的值域为 角度2 配方法求值域
【典例】求下列函数的值域 世纪金榜导学号
(1)f(x)=x2-2x+2.(2) f(x)= 【思维·引】
(1)先配方再求值域.
(2)先换元,再配方求值域.【解析】(1)函数的定义域为R,
因为f(x)=x2-2x+2=(x-1)2+1≥1,
所以函数的值域为[1,+∞).(2)因为函数有意义当且仅当x+1≥0,
即x≥-1,
故函数的定义域是[-1,+∞).
设t= 则x=t2-1(t≥0),于是g(t)=
又因为t≥0,故g(t)≥
所以函数的值域是 【类题·通】
求函数值域的常用方法
(1)利用不等式的性质:结合定义域,利用x的变形,推导解析式的范围.
(2)利用方程有解:设值域内的元素t,用t表示x,根据x的范围求t的范围,即值域.(3)配方法:是求“二次函数”类值域的基本方法.
(4)换元法:运用新元代换,将所给函数化成值域易确
定的函数,从而求得原函数的值域.对于f(x)=ax+b+
(其中a,b,c,d为常数,且ac≠0)型的函数常
用换元法.(5)分离常数法:此方法主要是针对分子分母同次的分式,即将分式转化为“反比例函数类”的形式,便于求值域.【发散·拓】
对于形如y= 的函数,还可以把已知函
数转化为关于变量的二次方程,再利用方程有解,即
判别式非负.从而求得原函数值域的方法叫判别式法.【延伸·练】
试用此法求函数y= 的值域.【解析】易知函数的定义域是R,
由y= 得yx2-x+y=0,
当y=0时,x=0,所以y可以为0;当y≠0时,Δ=1-4y2≥0,
所以
综上可得,所求函数的值域为 【习练·破】
(2019·天津高一检测)求下列函数的值域.
(1)f(x)= (2)y= 【解析】(1)f(x)= 的定义域为R,
x2+x+1=
所以
所以f(x)= 的值域为 (2)令t= (t≥0),则x=1-t2,换元可得函数的解
析式:g(t)=1-t2+4t
=-(t-2)2+5,又因为t≥0,故g(t)≤5,.
所以函数的值域是(-∞,5].【加练·固】
求下列函数的值域.
(1)y=
(2)y=
(3)y=3x2-x+2.【解析】(1)方法一:由x2≥0及4-x2≥0,
观察得 ∈[0,2],
故此函数的值域为[0,2].方法二:由 x2≥0得-x2≤0,得4-x2≤4,
所以0≤ ≤2,
故此函数的值域为[0,2].(2)y=
因为 所以y≠
所以函数的值域为 (3)函数y=
值域为
