2020版新教材高中数学第三章函数3.1.2.1函数的单调性课件新人教B版必修1:63张PPT
文档属性
| 名称 | 2020版新教材高中数学第三章函数3.1.2.1函数的单调性课件新人教B版必修1:63张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 23:05:15 | ||
图片预览










文档简介
课件63张PPT。3.1.2 函数的单调性
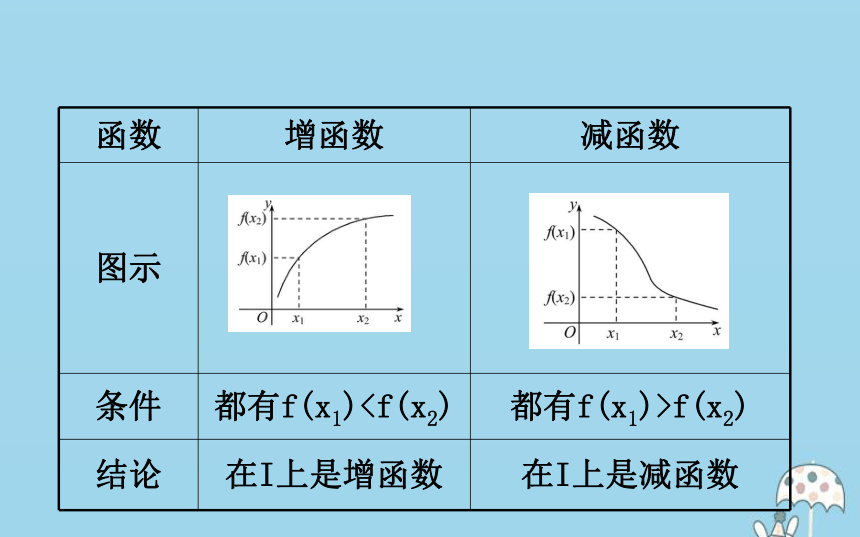
第1课时 函数的单调性1.函数单调性的定义
设函数y=f(x)的定义域为D,且I?D,如果对任意x1,x2∈I,当x1函数单调性的定义中,能否去掉“任意”?
提示:不能,不能用特殊代替一般.2.函数的单调性与单调区间
函数y=f(x)在区间I上是增函数或减函数,则函数在区间I上具有单调性,区间I叫函数的单调区间,分别称为单调递增区间或单调递减区间.【思考】
区间I一定是函数的定义域吗?
提示:不一定,可能是定义域的一个子区间,单调性是局部概念,不是整体概念.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)函数f(x)=2x2,若f(-1) ( )
(3)函数f(x)在定义域或其某一个子区间上一定有严格
的单调性. ( )提示:(1)×.函数f(x)=2x2在(0,+∞)上是增函数.
(2)×.函数f(x)= 的单调递减区间为(-∞,0),
(0,+∞),不能用“并”表示.
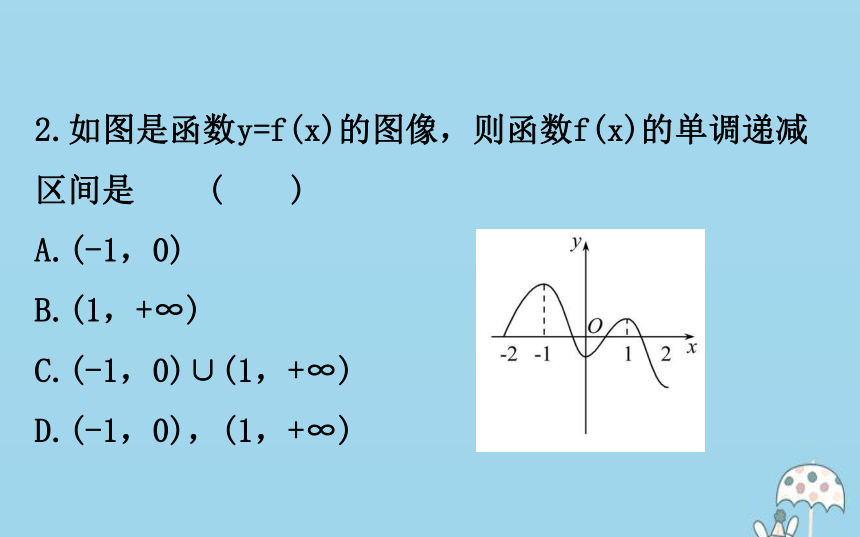
(3)×.常数函数不具有严格的单调性.2.如图是函数y=f(x)的图像,则函数f(x)的单调递减区间是 ( )
A.(-1,0)
B.(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-1,0),(1,+∞)【解析】选D.若函数单调递减,则对应图像为下降的,由图像知,函数在(-1,0),(1,+∞)上分别下降,则对应的单调递减区间为(-1,0),(1,+∞).3.若y=f(x)是定义在(-∞,+∞)上是减函数,且f(x)
所以由f(x)得x>2x-2,所以x<2,
所以x的取值范围为(-∞,2).
答案:(-∞,2)类型一 利用图像求函数的单调区间
【典例】1.如图是定义在区间[-2,2]的函数y=f(x),则f(x)的单调递减区间是________.?2.函数f(x)=x|x|-2x的单调递增区间为________.?【思维·引】
1.图像从左到右下降的区间为单调递减区间.
2.分情况去掉绝对值,作出图像确定单调递增区间.【解析】1.由图像可以看出f(x)的单调递减区间是
[-1,1].
答案:[-1,1]2.x≥0时,f(x)=x2-2x,对称轴为x=1,开口向上,在(1,+∞)单调递增,x<0时f(x)=-x2-2x,对称轴x=
-1,开口向下,在(-∞,-1)单调递增,
所以函数的单调递增区间是(-∞,-1)和(1,+∞).
答案:(-∞,-1)和(1,+∞)【内化·悟】
怎样求函数的单调区间?
提示:作出函数的图像,利用图像的上升、下降确定单调区间.【类题·通】
图像法求函数单调区间的步骤
①作图:作出函数的图像;
②结论:上升图像对应单调递增区间,下降图像对应单调递减区间.【习练·破】
函数f(x)=|x+2|的单调递增区间是________.?【解析】f(x)=|x+2|=
所以x≥-2时,f(x)=x+2单调递增,
所以f(x)的单调递增区间为[-2,+∞).
答案:[-2,+∞)【加练·固】
画出函数y=|x|(x-2)的图像,并指出函数的单调区间.【解析】y=|x|(x-2)=
函数的图像如图所示.由函数的图像知:函数的单调递增区间为(-∞,0]和[1,+∞),单调递减区间为(0,1).
类型二 利用定义证明函数的单调性
【典例】1.下列函数中,在R上是增函数的是 ( )
A.y=|x| B.y=x
C.y=x2 D.y= 2.证明函数f(x)=x- 在(0,+∞)上是增函数.
世纪金榜导学号【思维·引】1.考查当x增大时,函数值y的变化.
2.利用单调性的定义证明.【解析】1.选B.根据题意,依次分析选项:
对于A选项,y=|x|= 在R上不是增函数,不
符合题意;对于B选项,y=x,为正比例函数,在R上是增函数,符
合题意;
对于C选项,y=x2,为二次函数,在R上不是增函数,
不符合题意;
对于D选项,y= ,为反比例函数,在R上不是增函
数,不符合题意.2.任取x1,x2∈(0,+∞)且x1那么f(x1)-f(x2)= 因为x1,x2∈(0,+∞),
所以x1x2>0,所以1+ >0,
又x1-x2<0,所以f(x1)-f(x2)<0,即f(x1)所以f(x)在(0,+∞)上单调递增.【内化·悟】
如果函数是增函数,x与y的关系是什么?减函数呢?
提示:如果函数是增函数,当x增大时,y增大;
如果函数是减函数,当x增大时,y减小.【类题·通】
利用定义证明函数单调性的步骤【习练·破】
已知函数f(x)= (m<0),证明在(-∞,2)上是增
函数.【证明】任取x1,x2∈(-∞,2)且x1那么f(x1)-f(x2)=
由x1故f(x1)-f(x2)<0,即f(x1)故f(x)在(-∞,2)上单调递增.【加练·固】
证明:函数f(x)= 在(-∞,1)上是减函数.【证明】任取x1,x2∈(-∞,1)且x1则f(x1)-f(x2)=
因为x10,
又x1-x2<0,所以x2-x1>0,故f(x1)-f(x2)>0,即
f(x1)>f(x2),故f(x)在(-∞,1)上单调递减.类型三 函数单调性的简单应用
角度1 利用单调性解函数不等式
【典例】已知函数f(x)的定义域为[-2,2],且f(x)在区间[-2,2]上是增函数,f(1-m)所以 解得-1≤m≤2,
因为f(x)是增函数,所以1-m所以m>0.5,所以0.5答案:0.5 单调性的应用时,常常用到核心素养中的逻辑思维,利用单调性转化不等式,从而求出变量的范围.
本例的条件若改为“减函数”,试求m的取值范围.【解析】因为f(x)的定义域为[-2,2],
所以 解得-1≤m≤2,
因为f(x)是减函数,所以1-m>m,
所以m<0.5,所以-1≤m<0.5.
答案:-1≤m<0.5角度2 分段函数的单调性
【典例】若函数f(x)=
在R上为增函数,则实数b的取值范围为 ( )
世纪金榜导学号
A.[1,2] B.
C.(1,2] D. 【思维·引】分别考虑x>0,x<0,分界点三个方面的因素求范围.【解析】选A.因为函数f(x)=
在R上为增函数,所以 解得1≤b≤2.【类题·通】
由函数单调性求参数范围的类型及处理方法
(1)由函数解析式求参数(2)分段函数的单调性
首先分析每段上的单调性,其次是分界点处函数值的大小,如果是增函数,则界点左侧值小于等于右侧值,如果是减函数,则界点左侧值大于等于右侧值.【发散·拓】
关于“对勾”函数f(x)=x+ (a>0)的单调性.
函数y=x+ (a>0)的图像如图所示:则函数y=x+ 的单调增区间是(-∞,- ]和[ ,
+∞),单调减区间是(- ,0)和(0, ).【延伸·练】(2019·银川高一检测)函数f(x)=x+
(x>0)的单调减区间是 ( )
A.(2,+∞) B.(0,2)
C.( ,+∞) D.(0, )【解析】选D.函数f(x)=x+ (x>0),根据对勾函数图
像及性质可知,函数f(x)=x+ (x>0)在( ,+∞)单
调递增,函数f(x)在(0, )单调递减.【习练·破】
1.函数f(x)=kx2+(3k-2)x-5在[1,+∞)上单调递增,
则k的取值范围是 ( )
A.(0,+∞) B.
C. D. 【解析】选D.当k=0时,f(x)=-2x-5在R上单调递减,
不符合题意,当k≠0时,因为函数f(x)=kx2+(3k-2)x
-5在[1,+∞)上单调递增,所以 解得:
k≥ 综上所述,k的取值范围是 .2.若函数f(x)= 是(-∞,+∞)上的减
函数,则实数a的取值范围是________.?【解析】由题意,因为f(x)在R上是减函数,
x<0时f(x)=x2-ax+1,其过定点(0,1),
且x<0时是减函数,所以对称轴x= ≥0,①又因为x≥0时,f(x)=-x+3a,是减函数,且在R上是减
函数,所以3a≤1,②
由①②得0≤a≤
答案: 【加练·固】
已知函数f(x)=x2+ax+b.
(1)若函数f(x)的图像过点(1,4)和(2,5),求f(x)的解析式.
(2)若函数f(x)在区间[1,2]上不单调,求实数a的取值范围.【解析】(1)因为函数f(x)的图像过点(1,4)和(2,5),
所以 解得
所以f(x)=x2-2x+5.(2)函数f(x)的对称轴方程为x= 要使函数f(x)在
区间[1,2]上不单调,则1< <2,解得-4
第1课时 函数的单调性1.函数单调性的定义
设函数y=f(x)的定义域为D,且I?D,如果对任意x1,x2∈I,当x1
提示:不能,不能用特殊代替一般.2.函数的单调性与单调区间
函数y=f(x)在区间I上是增函数或减函数,则函数在区间I上具有单调性,区间I叫函数的单调区间,分别称为单调递增区间或单调递减区间.【思考】
区间I一定是函数的定义域吗?
提示:不一定,可能是定义域的一个子区间,单调性是局部概念,不是整体概念.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)函数f(x)=2x2,若f(-1)
(3)函数f(x)在定义域或其某一个子区间上一定有严格
的单调性. ( )提示:(1)×.函数f(x)=2x2在(0,+∞)上是增函数.
(2)×.函数f(x)= 的单调递减区间为(-∞,0),
(0,+∞),不能用“并”表示.
(3)×.常数函数不具有严格的单调性.2.如图是函数y=f(x)的图像,则函数f(x)的单调递减区间是 ( )
A.(-1,0)
B.(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-1,0),(1,+∞)【解析】选D.若函数单调递减,则对应图像为下降的,由图像知,函数在(-1,0),(1,+∞)上分别下降,则对应的单调递减区间为(-1,0),(1,+∞).3.若y=f(x)是定义在(-∞,+∞)上是减函数,且f(x)
所以x的取值范围为(-∞,2).
答案:(-∞,2)类型一 利用图像求函数的单调区间
【典例】1.如图是定义在区间[-2,2]的函数y=f(x),则f(x)的单调递减区间是________.?2.函数f(x)=x|x|-2x的单调递增区间为________.?【思维·引】
1.图像从左到右下降的区间为单调递减区间.
2.分情况去掉绝对值,作出图像确定单调递增区间.【解析】1.由图像可以看出f(x)的单调递减区间是
[-1,1].
答案:[-1,1]2.x≥0时,f(x)=x2-2x,对称轴为x=1,开口向上,在(1,+∞)单调递增,x<0时f(x)=-x2-2x,对称轴x=
-1,开口向下,在(-∞,-1)单调递增,
所以函数的单调递增区间是(-∞,-1)和(1,+∞).
答案:(-∞,-1)和(1,+∞)【内化·悟】
怎样求函数的单调区间?
提示:作出函数的图像,利用图像的上升、下降确定单调区间.【类题·通】
图像法求函数单调区间的步骤
①作图:作出函数的图像;
②结论:上升图像对应单调递增区间,下降图像对应单调递减区间.【习练·破】
函数f(x)=|x+2|的单调递增区间是________.?【解析】f(x)=|x+2|=
所以x≥-2时,f(x)=x+2单调递增,
所以f(x)的单调递增区间为[-2,+∞).
答案:[-2,+∞)【加练·固】
画出函数y=|x|(x-2)的图像,并指出函数的单调区间.【解析】y=|x|(x-2)=
函数的图像如图所示.由函数的图像知:函数的单调递增区间为(-∞,0]和[1,+∞),单调递减区间为(0,1).
类型二 利用定义证明函数的单调性
【典例】1.下列函数中,在R上是增函数的是 ( )
A.y=|x| B.y=x
C.y=x2 D.y= 2.证明函数f(x)=x- 在(0,+∞)上是增函数.
世纪金榜导学号【思维·引】1.考查当x增大时,函数值y的变化.
2.利用单调性的定义证明.【解析】1.选B.根据题意,依次分析选项:
对于A选项,y=|x|= 在R上不是增函数,不
符合题意;对于B选项,y=x,为正比例函数,在R上是增函数,符
合题意;
对于C选项,y=x2,为二次函数,在R上不是增函数,
不符合题意;
对于D选项,y= ,为反比例函数,在R上不是增函
数,不符合题意.2.任取x1,x2∈(0,+∞)且x1
所以x1x2>0,所以1+ >0,
又x1-x2<0,所以f(x1)-f(x2)<0,即f(x1)
如果函数是增函数,x与y的关系是什么?减函数呢?
提示:如果函数是增函数,当x增大时,y增大;
如果函数是减函数,当x增大时,y减小.【类题·通】
利用定义证明函数单调性的步骤【习练·破】
已知函数f(x)= (m<0),证明在(-∞,2)上是增
函数.【证明】任取x1,x2∈(-∞,2)且x1
由x1
证明:函数f(x)= 在(-∞,1)上是减函数.【证明】任取x1,x2∈(-∞,1)且x1
因为x1
又x1-x2<0,所以x2-x1>0,故f(x1)-f(x2)>0,即
f(x1)>f(x2),故f(x)在(-∞,1)上单调递减.类型三 函数单调性的简单应用
角度1 利用单调性解函数不等式
【典例】已知函数f(x)的定义域为[-2,2],且f(x)在区间[-2,2]上是增函数,f(1-m)
因为f(x)是增函数,所以1-m
本例的条件若改为“减函数”,试求m的取值范围.【解析】因为f(x)的定义域为[-2,2],
所以 解得-1≤m≤2,
因为f(x)是减函数,所以1-m>m,
所以m<0.5,所以-1≤m<0.5.
答案:-1≤m<0.5角度2 分段函数的单调性
【典例】若函数f(x)=
在R上为增函数,则实数b的取值范围为 ( )
世纪金榜导学号
A.[1,2] B.
C.(1,2] D. 【思维·引】分别考虑x>0,x<0,分界点三个方面的因素求范围.【解析】选A.因为函数f(x)=
在R上为增函数,所以 解得1≤b≤2.【类题·通】
由函数单调性求参数范围的类型及处理方法
(1)由函数解析式求参数(2)分段函数的单调性
首先分析每段上的单调性,其次是分界点处函数值的大小,如果是增函数,则界点左侧值小于等于右侧值,如果是减函数,则界点左侧值大于等于右侧值.【发散·拓】
关于“对勾”函数f(x)=x+ (a>0)的单调性.
函数y=x+ (a>0)的图像如图所示:则函数y=x+ 的单调增区间是(-∞,- ]和[ ,
+∞),单调减区间是(- ,0)和(0, ).【延伸·练】(2019·银川高一检测)函数f(x)=x+
(x>0)的单调减区间是 ( )
A.(2,+∞) B.(0,2)
C.( ,+∞) D.(0, )【解析】选D.函数f(x)=x+ (x>0),根据对勾函数图
像及性质可知,函数f(x)=x+ (x>0)在( ,+∞)单
调递增,函数f(x)在(0, )单调递减.【习练·破】
1.函数f(x)=kx2+(3k-2)x-5在[1,+∞)上单调递增,
则k的取值范围是 ( )
A.(0,+∞) B.
C. D. 【解析】选D.当k=0时,f(x)=-2x-5在R上单调递减,
不符合题意,当k≠0时,因为函数f(x)=kx2+(3k-2)x
-5在[1,+∞)上单调递增,所以 解得:
k≥ 综上所述,k的取值范围是 .2.若函数f(x)= 是(-∞,+∞)上的减
函数,则实数a的取值范围是________.?【解析】由题意,因为f(x)在R上是减函数,
x<0时f(x)=x2-ax+1,其过定点(0,1),
且x<0时是减函数,所以对称轴x= ≥0,①又因为x≥0时,f(x)=-x+3a,是减函数,且在R上是减
函数,所以3a≤1,②
由①②得0≤a≤
答案: 【加练·固】
已知函数f(x)=x2+ax+b.
(1)若函数f(x)的图像过点(1,4)和(2,5),求f(x)的解析式.
(2)若函数f(x)在区间[1,2]上不单调,求实数a的取值范围.【解析】(1)因为函数f(x)的图像过点(1,4)和(2,5),
所以 解得
所以f(x)=x2-2x+5.(2)函数f(x)的对称轴方程为x= 要使函数f(x)在
区间[1,2]上不单调,则1< <2,解得-4
