2020版新教材高中数学第三章函数3.1.3.1函数的奇偶性课件新人教B版必修1:62张PPT
文档属性
| 名称 | 2020版新教材高中数学第三章函数3.1.3.1函数的奇偶性课件新人教B版必修1:62张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览











文档简介
课件62张PPT。3.1.3 函数的奇偶性
第1课时 函数的奇偶性 1.函数的奇偶性【思考】
函数的奇偶性定义中,“对于定义域D内任意一个x,都有-x∈D”,那么奇偶函数的定义域有什么特征?
提示:奇偶函数的定义域关于原点对称.2.奇偶函数的图像特征
(1)函数是偶函数?图像关于y轴对称;
(2)函数是奇函数?图像关于原点对称.【思考】
(1)如果奇函数在原点处有定义,则其图像有什么特征?
提示:图像过原点,即f(0)=0.(2)有没有一个函数既是奇函数,又是偶函数?
提示:有.如f(x)=0的图像为x轴,即关于y轴对称,又关于原点对称,因此既是奇函数,又是偶函数.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)奇函数的图像一定过原点. ( )
(2)如果定义域内存在x0,满足f(-x0)=f(x0),
函数f(x)是偶函数. ( )(3)若对于定义域内的任意一个x,都有f(x)+
f(-x)=0,则函数f(x)是奇函数. ( )提示:(1)×.不一定,如函数f(x)= .
(2)×.不符合定义,必须对于定义域内的任意一个
x都成立.
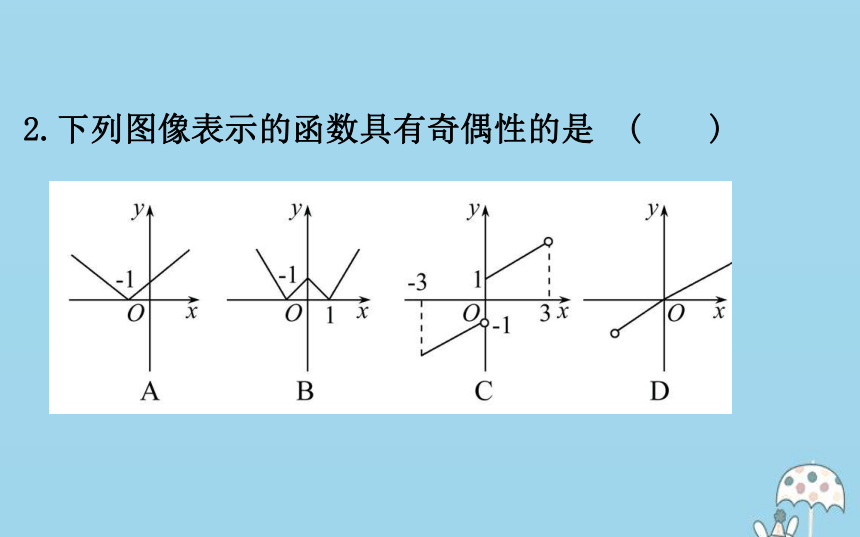
(3)√.若f(x)+f(-x)=0,则f(-x)=-f(x).2.下列图像表示的函数具有奇偶性的是 ( )【解析】选B.B选项的图像关于y轴对称,是偶函数,其余选项都不具有奇偶性.3.若f(x)为R上的奇函数,且f(2)=3,则f(-2)
=________. ?
【解析】因为f(x)为R上的奇函数,
所以f(-2)=-f(2)=-3.
答案:-3类型一 函数奇偶性的判断
【典例】1.函数f(x)= -2x的图像关于 ( )
A.y轴对称 B.坐标原点对称
C.直线y=-x对称 D.直线y=x对称2.判断下列函数的奇偶性: 世纪金榜导学号
(1)f(x)=|2x-1|-|2x+1|.
(2)f(x)= 【思维·引】1.先判断函数的奇偶性,再判断图像的对称性.
2.根据函数奇偶性的定义判断.【解析】1.选B.函数的定义域A={x|x≠0},
所以x∈A时,-x∈A,且f(-x)=- +2x
=- =-f(x),
所以f(x)为奇函数,故图像关于坐标原点对称.2.(1)因为x∈R,f(-x)=|-2x-1|-|-2x+1|
=-(|2x-1|-|2x+1|)=-f(x),所以f(x)是奇函数.(2)方法一:作出函数图像如图:
关于原点对称,所以函数是奇函数.方法二:当x>0时,f(x)=1-x2,此时-x<0,
所以f(-x)=(-x)2-1=x2-1,
所以f(-x)=-f(x);当x<0时,f(x)=x2-1,此时-x>0,
f(-x)=1-(-x)2=1-x2,
所以f(-x)=-f(x);当x=0时,f(-0)=-f(0)=0.
综上,对x∈R,总有f(-x)=-f(x),所以f(x)为R上
的奇函数.【内化·悟】
函数具有奇偶性的前提是什么?
提示:定义域关于原点对称.【类题·通】
判断函数奇偶性的两种方法
(1)定义法: (2)图像法:【发散·拓】
如果两个函数f(x),g(x)具有奇偶性,且有共同的
定义域,那么f(x)±g(x)、f(x)·g(x)、
(g(x)≠0)有以下规律:偶±偶=偶、奇±奇=奇、
偶×偶=偶、偶×奇=奇、奇×奇=偶,相除时类似于
相乘的情况.【延伸·练】
设f(x)是R上的任意函数,则下列叙述正确的是( )
A.f(x)f(-x)是奇函数
B.f(x)|f(-x)|是奇函数
C.f(x)-f(-x)是偶函数
D.f(x)+f(-x)是偶函数【解析】选D.当x∈R时,-x∈R,A中,
设g(x)=f(x)f(-x),则g(-x)=f(-x)·f(x)=g(x),
为偶函数;
B中,设g(x)=f(x)|f(-x)|,则g(-x)=f(-x)·
|f(x)|非奇非偶函数;C中,设g(x)=f(x)-f(-x),则g(-x)=f(-x)-f(x)
=-g(x),为奇函数;
D中,设g(x)=f(x)+f(-x),则g(-x)=f(-x)+f(x)
=g(x),所以f(x)+f(-x)是偶函数.【习练·破】
判断下列函数的奇偶性:
(1)f(x)= (2)f(x)=x3+x.
(3)f(x)= 【解析】(1)f(x)= 的定义域是A=(-∞,1)∪
(1,+∞),-1∈A,但1?A,所以f(x)为非奇非偶函数.
(2)f(x)=x3+x的定义域是R,当x∈R时,-x∈R,且
f(-x)=-f(x),所以f(x)为奇函数.(3)函数的定义域为R,当x∈R时,-x∈R,
当x>0时,-x<0,则f(-x)=-(-x)+1=x+1=f(x);
当x=0时,f(-x)=f(x)=1;
当x<0时,-x>0,f(-x)=-x+1=f(x).
综上,对任意x∈R,都有f(-x)=f(x),所以f(x)
为偶函数.【加练·固】
函数f(x)= -x2的图像关于 ( )
A.y轴对称
B.直线y=-x对称
C.坐标原点对称
D.直线y=x对称【解析】选A.f(x)的定义域为{x|x≠0},
又f(-x)= -(-x)2= -x2=f(x).
所以f(x)是偶函数,所以其图像关于y轴对称.类型二 奇偶函数图像的应用
【典例】1.如图,给出了奇函数f(x)的局部图像,
那么f(1)等于 ( )
A.-4 B.-2
C.2 D.42.设偶函数f(x)的定义域为[-5,5],且f(3)=0,当x∈[0,5]时,f(x)的图像如图所示,则不等式xf(x)<0的解集是________. 世纪金榜导学号?【思维·引】1.奇函数关于原点对称,点(-1,f(-1))的对称点为(1,-f(-1)).
2.利用偶函数的图像性质作出x∈[-5,0]上的图像,分两种情况讨论求不等式的解集.【解析】1.选B.由函数的图像可得f(-1)=2,又由函数为奇函数,则f(1)=-f(-1)=-2.2.因为f(x)为偶函数,且由图像可得在[0,3)上,
f(x)<0,在(3,5]上,f(x)>0,
则在[-5,-3)上,f(x)>0,在(-3,0]上,f(x)<0,
xf(x)<0? 所以-5≤x<-3或
0答案:[-5,-3)∪(0,3)【内化·悟】
怎样作具有奇偶性的函数的图像?
提示:先判断函数的奇偶性,作函数在y轴右侧的图像,根据奇偶性得到函数左侧的图像.【类题·通】
巧用奇偶性作函数图像的步骤
(1)确定函数的奇偶性.
(2)作出函数在[0,+∞)(或(-∞,0])上对应的图像.
(3)根据奇(偶)函数关于原点(y轴)对称得出在
(-∞,0](或[0,+∞))上对应的函数图像.【习练·破】
已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图像,如图所示.(1)请补出完整函数y=f(x)的图像.
(2)根据图像写出函数y=f(x)的增区间、值域.【解析】(1)由题意作出函数图像如图:(2)据图可知,单调增区间为(-1,0),(1,+∞),值域为[-1,+∞).【加练·固】
定义在R上的奇函数f(x)在[0,+∞)上的图像如图所示.
(1)画出f(x)的图像.
(2)写出函数的单调减区间.【解析】(1)先描出(1,1),(2,0)关于原点的对称点(-1,-1),(-2,0),连线可得f(x)的图像如图:(2)单调减区间为(-∞,-1],[1,+∞).类型三 利用奇偶性求参数值
角度1 利用奇偶性求参数值
【典例】已知函数f(x)=x3+(a+1)x2的图像关于原点对称,则a= 世纪金榜导学号( )
A.1 B.-1 C.-2 D.2【思维·引】根据图像,先得到奇偶性,再根据定义
求值.
【解析】选B.因为函数图像关于原点对称,
所以函数是奇函数,则f(-x)=-f(x),得-x3+(a+1)x2
=-x3-(a+1)x2,即(a+1)x2=0,即a+1=0,得a=-1.【素养·探】
在利用奇偶性的过程中,需要用到核心素养中的逻辑推理,将奇偶性转化为相应的等式,通过逻辑推理、计算求参数的值.
若将本例中的条件改为函数f(x)=ax2+(a-1)x+2是偶函数,试求a的值.【解析】若f(x)是偶函数,则f(-x)=f(x),
即k(-x)2-(k-1)x+2=kx2+(k-1)x+2,即(k-1)x=0
对于x∈R恒成立,则k-1=0,k=1.角度2 利用奇偶性求函数值
【典例】1.已知函数f(x)=ax3+bx-2,f(2 019)=3,
则f(-2 019)= 世纪金榜导学号( )
A.-7 B.-5 C.-3 D.-22.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x+1,则f(1)+g(1)=( )
A.-3 B.-1 C.1 D.3【思维·引】1.利用f(2 019)=3求出未知式子的值,再求f(-2 019)的值.
2.利用奇偶函数的定义,构造f(x)+g(x)后求值.【解析】1.选A.因为f(2 019)=3,
所以f(2 019)=2 0193a+2 019b-2=3,
所以2 0193a+2 019b=5,
所以f(-2 019)=-2 0193a-2 019b-2=-5-2=-7.2.选B.由f(x)-g(x)=x3+x+1,将所有x替换成-x,得
f(-x)-g(-x)=-x3-x+1,根据f(x)=f(-x),g(-x)=
-g(x),得f(x)+g(x)=-x3-x+1,再令x=1,计算得,
f(1)+g(1)=-1.【类题·通】
利用奇偶性求参数的常见类型及策略
(1)定义域含参数:奇、偶函数f(x)的定义域为
[a,b],根据定义域关于原点对称,a+b=0求参数.
(2)解析式含参数:根据f(-x)=-f(x)或f(-x)=f(x)
列式,比较系数即可求解.【习练·破】
1.已知函数f(x)是定义在R上的奇函数,且当x>1时,
f(x)= -1,则f(-2)= ( )
【解析】选B.根据题意,当x>1时,f(x)= -1,
则f(2)= -1= ,又由函数f(x)为奇函数,
则f(-2)=-f(2)=- .2.已知函数f(x)=ax2+bx+c(-2a-3≤x≤1)是偶函数,则a=________,b=________.?【解析】因为f(x)是偶函数,所以其定义域关于y轴对
称.所以-2a-3=-1.所以a=-1.所以f(x)=-x2+bx+c.因为
f(-x)=f(x),所以-(-x)2+b(-x)+c=-x2+bx+c.所以
-b=b,所以b=0.
答案:-1 0【加练·固】
若f(x)=ax2+bx+c(a≠0)是偶函数,则g(x)=ax3+bx2+cx是 ( )
A.奇函数 B.偶函数
C.非奇非偶函数 D.既是奇函数又是偶函数【解析】选A.因为f(x)=ax2+bx+c(a≠0)是偶函数,
所以f(x)=f(-x),即ax2+bx+c=ax2-bx+c,所以b=0,
所以g(x)=ax3+bx2+cx=ax3+cx,所以g(-x)=-(ax3+cx)
=-g(x),所以g(x)是奇函数.
第1课时 函数的奇偶性 1.函数的奇偶性【思考】
函数的奇偶性定义中,“对于定义域D内任意一个x,都有-x∈D”,那么奇偶函数的定义域有什么特征?
提示:奇偶函数的定义域关于原点对称.2.奇偶函数的图像特征
(1)函数是偶函数?图像关于y轴对称;
(2)函数是奇函数?图像关于原点对称.【思考】
(1)如果奇函数在原点处有定义,则其图像有什么特征?
提示:图像过原点,即f(0)=0.(2)有没有一个函数既是奇函数,又是偶函数?
提示:有.如f(x)=0的图像为x轴,即关于y轴对称,又关于原点对称,因此既是奇函数,又是偶函数.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)奇函数的图像一定过原点. ( )
(2)如果定义域内存在x0,满足f(-x0)=f(x0),
函数f(x)是偶函数. ( )(3)若对于定义域内的任意一个x,都有f(x)+
f(-x)=0,则函数f(x)是奇函数. ( )提示:(1)×.不一定,如函数f(x)= .
(2)×.不符合定义,必须对于定义域内的任意一个
x都成立.
(3)√.若f(x)+f(-x)=0,则f(-x)=-f(x).2.下列图像表示的函数具有奇偶性的是 ( )【解析】选B.B选项的图像关于y轴对称,是偶函数,其余选项都不具有奇偶性.3.若f(x)为R上的奇函数,且f(2)=3,则f(-2)
=________. ?
【解析】因为f(x)为R上的奇函数,
所以f(-2)=-f(2)=-3.
答案:-3类型一 函数奇偶性的判断
【典例】1.函数f(x)= -2x的图像关于 ( )
A.y轴对称 B.坐标原点对称
C.直线y=-x对称 D.直线y=x对称2.判断下列函数的奇偶性: 世纪金榜导学号
(1)f(x)=|2x-1|-|2x+1|.
(2)f(x)= 【思维·引】1.先判断函数的奇偶性,再判断图像的对称性.
2.根据函数奇偶性的定义判断.【解析】1.选B.函数的定义域A={x|x≠0},
所以x∈A时,-x∈A,且f(-x)=- +2x
=- =-f(x),
所以f(x)为奇函数,故图像关于坐标原点对称.2.(1)因为x∈R,f(-x)=|-2x-1|-|-2x+1|
=-(|2x-1|-|2x+1|)=-f(x),所以f(x)是奇函数.(2)方法一:作出函数图像如图:
关于原点对称,所以函数是奇函数.方法二:当x>0时,f(x)=1-x2,此时-x<0,
所以f(-x)=(-x)2-1=x2-1,
所以f(-x)=-f(x);当x<0时,f(x)=x2-1,此时-x>0,
f(-x)=1-(-x)2=1-x2,
所以f(-x)=-f(x);当x=0时,f(-0)=-f(0)=0.
综上,对x∈R,总有f(-x)=-f(x),所以f(x)为R上
的奇函数.【内化·悟】
函数具有奇偶性的前提是什么?
提示:定义域关于原点对称.【类题·通】
判断函数奇偶性的两种方法
(1)定义法: (2)图像法:【发散·拓】
如果两个函数f(x),g(x)具有奇偶性,且有共同的
定义域,那么f(x)±g(x)、f(x)·g(x)、
(g(x)≠0)有以下规律:偶±偶=偶、奇±奇=奇、
偶×偶=偶、偶×奇=奇、奇×奇=偶,相除时类似于
相乘的情况.【延伸·练】
设f(x)是R上的任意函数,则下列叙述正确的是( )
A.f(x)f(-x)是奇函数
B.f(x)|f(-x)|是奇函数
C.f(x)-f(-x)是偶函数
D.f(x)+f(-x)是偶函数【解析】选D.当x∈R时,-x∈R,A中,
设g(x)=f(x)f(-x),则g(-x)=f(-x)·f(x)=g(x),
为偶函数;
B中,设g(x)=f(x)|f(-x)|,则g(-x)=f(-x)·
|f(x)|非奇非偶函数;C中,设g(x)=f(x)-f(-x),则g(-x)=f(-x)-f(x)
=-g(x),为奇函数;
D中,设g(x)=f(x)+f(-x),则g(-x)=f(-x)+f(x)
=g(x),所以f(x)+f(-x)是偶函数.【习练·破】
判断下列函数的奇偶性:
(1)f(x)= (2)f(x)=x3+x.
(3)f(x)= 【解析】(1)f(x)= 的定义域是A=(-∞,1)∪
(1,+∞),-1∈A,但1?A,所以f(x)为非奇非偶函数.
(2)f(x)=x3+x的定义域是R,当x∈R时,-x∈R,且
f(-x)=-f(x),所以f(x)为奇函数.(3)函数的定义域为R,当x∈R时,-x∈R,
当x>0时,-x<0,则f(-x)=-(-x)+1=x+1=f(x);
当x=0时,f(-x)=f(x)=1;
当x<0时,-x>0,f(-x)=-x+1=f(x).
综上,对任意x∈R,都有f(-x)=f(x),所以f(x)
为偶函数.【加练·固】
函数f(x)= -x2的图像关于 ( )
A.y轴对称
B.直线y=-x对称
C.坐标原点对称
D.直线y=x对称【解析】选A.f(x)的定义域为{x|x≠0},
又f(-x)= -(-x)2= -x2=f(x).
所以f(x)是偶函数,所以其图像关于y轴对称.类型二 奇偶函数图像的应用
【典例】1.如图,给出了奇函数f(x)的局部图像,
那么f(1)等于 ( )
A.-4 B.-2
C.2 D.42.设偶函数f(x)的定义域为[-5,5],且f(3)=0,当x∈[0,5]时,f(x)的图像如图所示,则不等式xf(x)<0的解集是________. 世纪金榜导学号?【思维·引】1.奇函数关于原点对称,点(-1,f(-1))的对称点为(1,-f(-1)).
2.利用偶函数的图像性质作出x∈[-5,0]上的图像,分两种情况讨论求不等式的解集.【解析】1.选B.由函数的图像可得f(-1)=2,又由函数为奇函数,则f(1)=-f(-1)=-2.2.因为f(x)为偶函数,且由图像可得在[0,3)上,
f(x)<0,在(3,5]上,f(x)>0,
则在[-5,-3)上,f(x)>0,在(-3,0]上,f(x)<0,
xf(x)<0? 所以-5≤x<-3或
0
怎样作具有奇偶性的函数的图像?
提示:先判断函数的奇偶性,作函数在y轴右侧的图像,根据奇偶性得到函数左侧的图像.【类题·通】
巧用奇偶性作函数图像的步骤
(1)确定函数的奇偶性.
(2)作出函数在[0,+∞)(或(-∞,0])上对应的图像.
(3)根据奇(偶)函数关于原点(y轴)对称得出在
(-∞,0](或[0,+∞))上对应的函数图像.【习练·破】
已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图像,如图所示.(1)请补出完整函数y=f(x)的图像.
(2)根据图像写出函数y=f(x)的增区间、值域.【解析】(1)由题意作出函数图像如图:(2)据图可知,单调增区间为(-1,0),(1,+∞),值域为[-1,+∞).【加练·固】
定义在R上的奇函数f(x)在[0,+∞)上的图像如图所示.
(1)画出f(x)的图像.
(2)写出函数的单调减区间.【解析】(1)先描出(1,1),(2,0)关于原点的对称点(-1,-1),(-2,0),连线可得f(x)的图像如图:(2)单调减区间为(-∞,-1],[1,+∞).类型三 利用奇偶性求参数值
角度1 利用奇偶性求参数值
【典例】已知函数f(x)=x3+(a+1)x2的图像关于原点对称,则a= 世纪金榜导学号( )
A.1 B.-1 C.-2 D.2【思维·引】根据图像,先得到奇偶性,再根据定义
求值.
【解析】选B.因为函数图像关于原点对称,
所以函数是奇函数,则f(-x)=-f(x),得-x3+(a+1)x2
=-x3-(a+1)x2,即(a+1)x2=0,即a+1=0,得a=-1.【素养·探】
在利用奇偶性的过程中,需要用到核心素养中的逻辑推理,将奇偶性转化为相应的等式,通过逻辑推理、计算求参数的值.
若将本例中的条件改为函数f(x)=ax2+(a-1)x+2是偶函数,试求a的值.【解析】若f(x)是偶函数,则f(-x)=f(x),
即k(-x)2-(k-1)x+2=kx2+(k-1)x+2,即(k-1)x=0
对于x∈R恒成立,则k-1=0,k=1.角度2 利用奇偶性求函数值
【典例】1.已知函数f(x)=ax3+bx-2,f(2 019)=3,
则f(-2 019)= 世纪金榜导学号( )
A.-7 B.-5 C.-3 D.-22.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x+1,则f(1)+g(1)=( )
A.-3 B.-1 C.1 D.3【思维·引】1.利用f(2 019)=3求出未知式子的值,再求f(-2 019)的值.
2.利用奇偶函数的定义,构造f(x)+g(x)后求值.【解析】1.选A.因为f(2 019)=3,
所以f(2 019)=2 0193a+2 019b-2=3,
所以2 0193a+2 019b=5,
所以f(-2 019)=-2 0193a-2 019b-2=-5-2=-7.2.选B.由f(x)-g(x)=x3+x+1,将所有x替换成-x,得
f(-x)-g(-x)=-x3-x+1,根据f(x)=f(-x),g(-x)=
-g(x),得f(x)+g(x)=-x3-x+1,再令x=1,计算得,
f(1)+g(1)=-1.【类题·通】
利用奇偶性求参数的常见类型及策略
(1)定义域含参数:奇、偶函数f(x)的定义域为
[a,b],根据定义域关于原点对称,a+b=0求参数.
(2)解析式含参数:根据f(-x)=-f(x)或f(-x)=f(x)
列式,比较系数即可求解.【习练·破】
1.已知函数f(x)是定义在R上的奇函数,且当x>1时,
f(x)= -1,则f(-2)= ( )
【解析】选B.根据题意,当x>1时,f(x)= -1,
则f(2)= -1= ,又由函数f(x)为奇函数,
则f(-2)=-f(2)=- .2.已知函数f(x)=ax2+bx+c(-2a-3≤x≤1)是偶函数,则a=________,b=________.?【解析】因为f(x)是偶函数,所以其定义域关于y轴对
称.所以-2a-3=-1.所以a=-1.所以f(x)=-x2+bx+c.因为
f(-x)=f(x),所以-(-x)2+b(-x)+c=-x2+bx+c.所以
-b=b,所以b=0.
答案:-1 0【加练·固】
若f(x)=ax2+bx+c(a≠0)是偶函数,则g(x)=ax3+bx2+cx是 ( )
A.奇函数 B.偶函数
C.非奇非偶函数 D.既是奇函数又是偶函数【解析】选A.因为f(x)=ax2+bx+c(a≠0)是偶函数,
所以f(x)=f(-x),即ax2+bx+c=ax2-bx+c,所以b=0,
所以g(x)=ax3+bx2+cx=ax3+cx,所以g(-x)=-(ax3+cx)
=-g(x),所以g(x)是奇函数.
