2020版新教材高中数学第一章集合与常用逻辑用语1.1.3.1交集、并集课件新人教B版必修1:81张PPT
文档属性
| 名称 | 2020版新教材高中数学第一章集合与常用逻辑用语1.1.3.1交集、并集课件新人教B版必修1:81张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 23:11:20 | ||
图片预览










文档简介
课件81张PPT。1.1.3 集合的基本运算
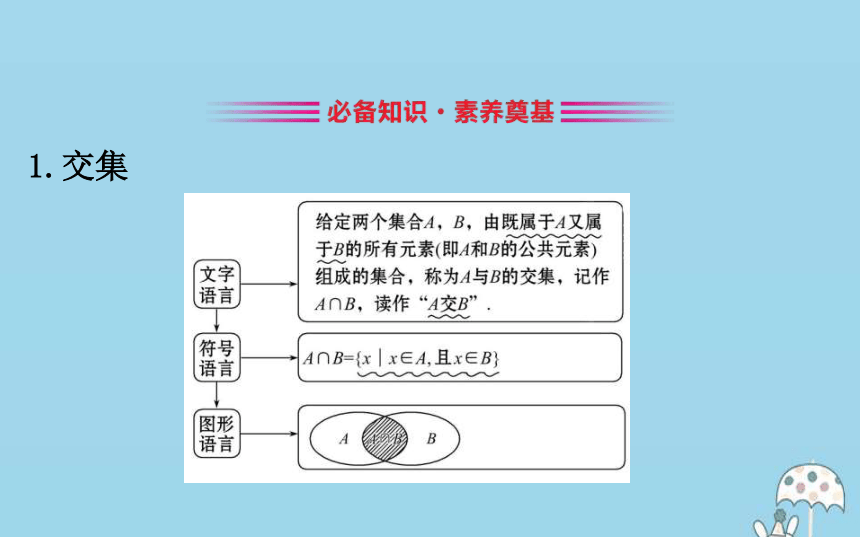
第1课时 交集、并集 1.交集【思考】
当集合A,B无公共元素时,A与B有交集吗?
提示:当集合A,B无公共元素时,A与B有交集,它们的交集是空集.2.并集【思考】
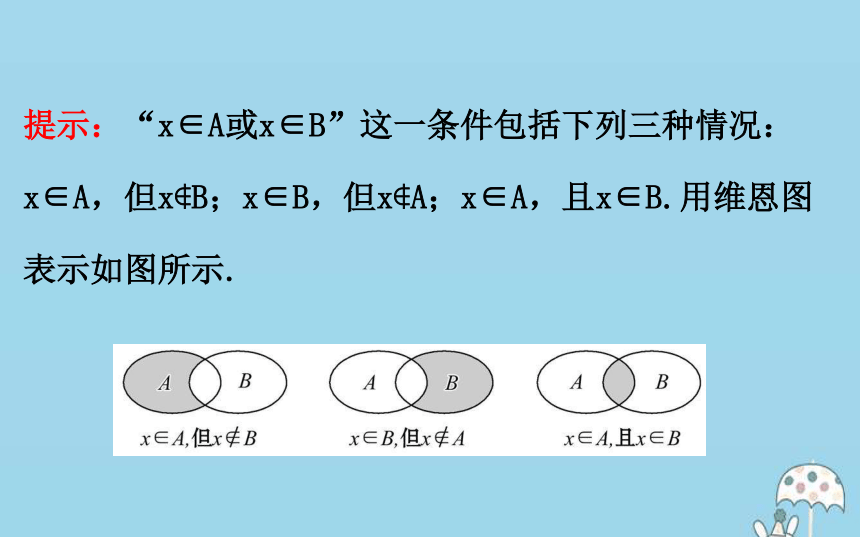
(1)“x∈A或x∈B”包含哪几种情况?如何用维恩图表示?提示:“x∈A或x∈B”这一条件包括下列三种情况:x∈A,但x?B;x∈B,但x?A;x∈A,且x∈B.用维恩图表示如图所示.(2)集合A∪B的元素个数是否等于集合A与集合B的元素个数和?提示:不一定等于.A∪B的元素个数小于或等于集合A与集合B的元素个数和.3.交集与并集的运算性质【思考】
对于任意两个集合A,B,A∩B与A有什么关系?A∪B 与A有什么关系??
提示:(A∩B)?A,A?(A∪B).【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)集合A和集合B的公共元素组成的集合就是集合A与B的交集. ( )
(2)若A∩B=?,则A,B均为空集. ( )(3)A,B中分别有3个元素,则A∪B中必有6个元素.
( )
(4)若x∈A∩B,则x∈A∪B. ( )提示:(1)√.根据交集的定义可知此说法正确.
(2)×.当A∩B=?时,A,B可以为?,也可以不为?,如A={1,2},B={3,4},A∩B=?.(3)×.求两个集合的并集时,这两个集合的公共元素在并集中只能出现一次,需要满足集合中元素的互异性.所以A,B中分别有3个元素,则A∪B中的元素个数可能是3,4,5,6个.
(4)√.因为(A∩B)?(A∪B).2.已知集合M={-1,0,1},N={0,1,2},则M∪N=
( )
A.{0,1} B.{-1,0,2}
C.{-1,0,1,2} D.{-1,0,1}【解析】选C.M∪N={-1,0,1,2}.3.设集合M=(-3,2),N=[1,3],则M∩N= ( )
A.[1,2) B.[1,2]
C.(2,3] D.[2,3]【解析】选A.因为M=(-3,2)且N=[1,3],
所以M∩N=[1,2).类型一 交集概念及其应用
【典例】1.(2018·全国卷Ⅰ)已知集合A={0,2},B={-2,-1,0,1,2},则A∩B= ( )
A.{0,2} B.{1,2}
C.{0} D.{-2,-1,0,1,2}2.已知A={x|x≤-2或x>5},B={x|13.集合A=[-2,5],集合B =[m+1,2m-1],世纪金榜导学号
(1)若B?A,求实数m的取值范围.
(2)若A∩B≠?,求实数m的取值范围.【思维·引】1.找集合A,B的公共元素,写出A∩B.
2.在数轴上表示集合A,B,观察图形,根据交集的定义写出A∩B.3.(1)分当B=?和B≠?两种情况讨论.
(2)先求出A∩B=?时实数m的取值范围,再写出A∩B≠?时实数m的取值范围.【解析】1.选A.A∩B={0,2}.2.将集合A和B在数轴上表示出来.根据交集的定义,图中阴影部分即为所求,所以A∩B=(5,7].
答案:(5,7]3.(1)当B=?时,B?A,此时m+1>2m-1,
解得m<2,
当B≠?时,为使B?A,m需满足解得2≤m≤3,
综上知实数m的取值范围为(-∞,3].(2)先求A∩B=?,当B=?时由(1)知m<2,当B≠?时,为
使A∩B=?,m需满足
或 ,解得m>4,
综上知当m<2或m>4时A∩B=?,
所以若A∩B≠?,实数m的取值范围是[2,4].【内化·悟】
画数轴求两个集合的交集时,要注意哪些问题?
提示:(1)两个集合的交集是表示两个集合的图形所覆盖的公共范围.(2)注意端点处的“实”与“虚”.【类题·通】
1.求集合A∩B的步骤
(1)要清楚集合A,B的元素是什么.
(2)把所求交集用集合符号表示出来,写成“A∩B”的形式.(3)把化简后的集合A,B的所有公共元素都写出来即可(相同元素只写一个).2.求集合A∩B的常用方法
(1)若A,B的代表元素是方程的根,则应先解方程求出方程的根后,再求两集合的交集.(2)若集合的代表元素是有序数对,则A∩B是指两个方程组成的方程组的解集,解集是点集.
(3)若A,B是无限数集,可以利用数轴来求解,但要注意“实”“虚”点.【习练·破】
1.已知集合P=(-∞,0),Q=(-∞,1],则P∩Q=________.?【解析】因为P=(-∞,0),Q=(-∞,1],
故P∩Q=(-∞,0).
答案:(-∞,0)2.已知集合A={a2,a+1,-3},B={a-3,2a-1,a2+1},若A∩B={-3},求实数a的值.【解析】因为A∩B={-3},所以-3∈B.
而a2+1≠-3,所以a-3=-3或2a-1=-3.(1)当a-3=-3时,a=0.
A={0,1,-3},B={-3,-1,1},于是A∩B={-3,1},这样与A∩B={-3}矛盾;
(2)当2a-1=-3时,a=-1,符合A∩B={-3},综上知a=-1.【加练·固】
已知集合M=(-∞,a],N=(-2,0),若M∩N=?,则a的取值范围为 ( )
A.(0,+∞) B.[0,+∞)
C.(-∞,-2) D.(-∞,-2]【解析】选D.画数轴可知,当M∩N=?时,a的取值范围是(-∞,-2].类型二 并集概念及其应用
【典例】1.设集合M={x|x2+2x=0,x∈R},N={x|x2-2x=0,x∈R},则M∪N= ( )
A.{0} B.{0,2}
C.{-2,0} D.{-2,0,2}2.已知集合M={x|-35},则M∪N= ( )
A.{x|x<-5或x>-3} B.{x|-5C.{x|-35}3.设S={x|x<-1或x>5},T={x|a世纪金榜导学号
A.-3C.a≤-3或a>-1 D.a<-3或a>-1【思维·引】1.列举法表示集合M,N,根据并集的定义写出M∪N.
2.在数轴上表示集合M,N,观察图形根据并集的定义写出M∪N.
3.在数轴上表示集合S,T,观察图形并根据S∪T=R列出不等式组,求解得实数a应满足的条件.【解析】1.选D.M={x|x2+2x=0,x∈R}={0,-2},N={x|x2-2x=0,x∈R}={0,2},故M∪N={-2,0,2}.2.选A.在数轴上表示集合M,N,如图所示, 则M∪N={x|x<-5或x>-3}.3.选A.在数轴上表示集合S,T如图所示.因为S∪T=R,由数轴可得
解得-31.用数轴如何表示下列集合?
(1){x|xb}.
(3){x|xb(ab}(3){x|xb(a提示:(1)两个集合的并集是表示两个集合的图形所覆盖的全部范围.
(2)注意当端点不在集合中时,应用“空心点”表示,当端点在集合中时,应用“实心点”表示.【类题·通】
求集合并集的方法
(1)两集合用列举法给出:①依定义,直接观察求并集;②借助维恩图写并集.
(2)两集合用描述法给出:①直接观察,写出并集;
②借助数轴,求出并集.(3)一个集合用描述法,另一个用列举法:①直接观察,找出并集;②借助图形,观察写出并集.
提醒:若两个集合中有相同元素,在求其并集时,只能算作一个.【习练·破】
1.满足条件{1,2}∪M={1,2,3}的所有集合M的个数是 ( )
A.1 B.2
C.3 D.4【解析】选D.因为{1,2}∪M={1,2,3},
所以3∈M,则满足条件的M可以是{3}或{1,3}或{2,3}或{1,2,3},共有4个.2.若集合A=(-∞,1],B=[0,+∞),则A∪B=_______.?【解析】如图所以A∪B=R.
答案:R【加练·固】
点集A={(x,y)|x<0},B={(x,y)|y<0},则A∪B中的元素不可能在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限【解析】选A.由题意得,A∪B中的元素是由横坐标小于0或纵坐标小于0的点构成的集合,所以A∪B中的元素不可能在第一象限.类型三 集合交、并运算的性质及综合应用
【典例】已知A={x|a≤x≤a+3},B={x|x<-1或x>5}.
世纪金榜导学号
(1)若A∩B=?,求实数a的取值范围.
(2)若A∪B=B,求实数a的取值范围.【思维·引】(1)根据A∩B=?列不等式组,求实数a的取值范围.
(2)由A∪B=B,推出A?B,列不等式求实数a的取值范围.【解析】(1)因为A∩B=?,所以
解得-1≤a≤2,所以实数a的取值范围是[-1,2].(2)因为A∪B=B,所以A?B,
所以a>5或a+3<-1,
即a的取值范围为a>5或a<-4,
所以实数a的取值范围是(-∞,-4)∪(5,+∞).【素养·探】
交集、并集运算性质的应用问题中,经常利用核心素养中的直观想象,常利用维恩图或数轴直观展示,根据集合运算结果分析集合之间的关系并列出不等式(组),求参数的值或范围.本例中若将条件改为A={x|-3(1)当B=?,即k+1>2k-1时,k<2,满足B?A;(2)当B≠?时,要使B?A,只需
解得2≤k≤ .综合(1)(2)可知k的取值范围是【类题·通】
1.集合运算常用的性质
(1)A∪B=B?A?B.(2)A∩B=A?A?B.
(3)A∩B=A∪B?A=B.2.利用集合交集、并集的性质解题的方法及关注点
(1)方法:利用集合的交集、并集性质解题时,常常遇到A∪B=B,A∩B=A等问题,解答时常借助于交集、并集的定义及已知集合间的关系去转化为集合间的关系求解.(2)关注点:当集合A?B时,若集合A不确定,运算时要考虑A=?的情况,否则易漏解.【习练·破】
1.(2018·天津高考)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C=( )
A.{-1,1} B.{0,1}
C.{-1,0,1} D.{2,3,4}【解析】选C.因为集合A={1,2,3,4},
B={-1,0,2,3},A∪B={-1,0,1,2,3,4},
所以(A∪B)∩C={-1,0,1}.2. 集合A={x|x2-3x+2=0},B={x|x2-2x+a-1=0},A∩B=B,求a的取值范围.【解析】由题意,得A={1,2},因为A∩B=B,
当B=?时,(-2)2-4(a-1)<0,解得a>2;
当1∈B时,1-2+a-1=0,
解得a=2,且此时B={1},符合题意;当2∈B时,4-4+a-1=0,
解得a=1,此时B={0,2},不合题意;
当1∈B且2∈B时,此时a无解.综上所述,a的取值范围是[2,+∞).
第1课时 交集、并集 1.交集【思考】
当集合A,B无公共元素时,A与B有交集吗?
提示:当集合A,B无公共元素时,A与B有交集,它们的交集是空集.2.并集【思考】
(1)“x∈A或x∈B”包含哪几种情况?如何用维恩图表示?提示:“x∈A或x∈B”这一条件包括下列三种情况:x∈A,但x?B;x∈B,但x?A;x∈A,且x∈B.用维恩图表示如图所示.(2)集合A∪B的元素个数是否等于集合A与集合B的元素个数和?提示:不一定等于.A∪B的元素个数小于或等于集合A与集合B的元素个数和.3.交集与并集的运算性质【思考】
对于任意两个集合A,B,A∩B与A有什么关系?A∪B 与A有什么关系??
提示:(A∩B)?A,A?(A∪B).【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)集合A和集合B的公共元素组成的集合就是集合A与B的交集. ( )
(2)若A∩B=?,则A,B均为空集. ( )(3)A,B中分别有3个元素,则A∪B中必有6个元素.
( )
(4)若x∈A∩B,则x∈A∪B. ( )提示:(1)√.根据交集的定义可知此说法正确.
(2)×.当A∩B=?时,A,B可以为?,也可以不为?,如A={1,2},B={3,4},A∩B=?.(3)×.求两个集合的并集时,这两个集合的公共元素在并集中只能出现一次,需要满足集合中元素的互异性.所以A,B中分别有3个元素,则A∪B中的元素个数可能是3,4,5,6个.
(4)√.因为(A∩B)?(A∪B).2.已知集合M={-1,0,1},N={0,1,2},则M∪N=
( )
A.{0,1} B.{-1,0,2}
C.{-1,0,1,2} D.{-1,0,1}【解析】选C.M∪N={-1,0,1,2}.3.设集合M=(-3,2),N=[1,3],则M∩N= ( )
A.[1,2) B.[1,2]
C.(2,3] D.[2,3]【解析】选A.因为M=(-3,2)且N=[1,3],
所以M∩N=[1,2).类型一 交集概念及其应用
【典例】1.(2018·全国卷Ⅰ)已知集合A={0,2},B={-2,-1,0,1,2},则A∩B= ( )
A.{0,2} B.{1,2}
C.{0} D.{-2,-1,0,1,2}2.已知A={x|x≤-2或x>5},B={x|1
(1)若B?A,求实数m的取值范围.
(2)若A∩B≠?,求实数m的取值范围.【思维·引】1.找集合A,B的公共元素,写出A∩B.
2.在数轴上表示集合A,B,观察图形,根据交集的定义写出A∩B.3.(1)分当B=?和B≠?两种情况讨论.
(2)先求出A∩B=?时实数m的取值范围,再写出A∩B≠?时实数m的取值范围.【解析】1.选A.A∩B={0,2}.2.将集合A和B在数轴上表示出来.根据交集的定义,图中阴影部分即为所求,所以A∩B=(5,7].
答案:(5,7]3.(1)当B=?时,B?A,此时m+1>2m-1,
解得m<2,
当B≠?时,为使B?A,m需满足解得2≤m≤3,
综上知实数m的取值范围为(-∞,3].(2)先求A∩B=?,当B=?时由(1)知m<2,当B≠?时,为
使A∩B=?,m需满足
或 ,解得m>4,
综上知当m<2或m>4时A∩B=?,
所以若A∩B≠?,实数m的取值范围是[2,4].【内化·悟】
画数轴求两个集合的交集时,要注意哪些问题?
提示:(1)两个集合的交集是表示两个集合的图形所覆盖的公共范围.(2)注意端点处的“实”与“虚”.【类题·通】
1.求集合A∩B的步骤
(1)要清楚集合A,B的元素是什么.
(2)把所求交集用集合符号表示出来,写成“A∩B”的形式.(3)把化简后的集合A,B的所有公共元素都写出来即可(相同元素只写一个).2.求集合A∩B的常用方法
(1)若A,B的代表元素是方程的根,则应先解方程求出方程的根后,再求两集合的交集.(2)若集合的代表元素是有序数对,则A∩B是指两个方程组成的方程组的解集,解集是点集.
(3)若A,B是无限数集,可以利用数轴来求解,但要注意“实”“虚”点.【习练·破】
1.已知集合P=(-∞,0),Q=(-∞,1],则P∩Q=________.?【解析】因为P=(-∞,0),Q=(-∞,1],
故P∩Q=(-∞,0).
答案:(-∞,0)2.已知集合A={a2,a+1,-3},B={a-3,2a-1,a2+1},若A∩B={-3},求实数a的值.【解析】因为A∩B={-3},所以-3∈B.
而a2+1≠-3,所以a-3=-3或2a-1=-3.(1)当a-3=-3时,a=0.
A={0,1,-3},B={-3,-1,1},于是A∩B={-3,1},这样与A∩B={-3}矛盾;
(2)当2a-1=-3时,a=-1,符合A∩B={-3},综上知a=-1.【加练·固】
已知集合M=(-∞,a],N=(-2,0),若M∩N=?,则a的取值范围为 ( )
A.(0,+∞) B.[0,+∞)
C.(-∞,-2) D.(-∞,-2]【解析】选D.画数轴可知,当M∩N=?时,a的取值范围是(-∞,-2].类型二 并集概念及其应用
【典例】1.设集合M={x|x2+2x=0,x∈R},N={x|x2-2x=0,x∈R},则M∪N= ( )
A.{0} B.{0,2}
C.{-2,0} D.{-2,0,2}2.已知集合M={x|-3
A.{x|x<-5或x>-3} B.{x|-5
A.-3
2.在数轴上表示集合M,N,观察图形根据并集的定义写出M∪N.
3.在数轴上表示集合S,T,观察图形并根据S∪T=R列出不等式组,求解得实数a应满足的条件.【解析】1.选D.M={x|x2+2x=0,x∈R}={0,-2},N={x|x2-2x=0,x∈R}={0,2},故M∪N={-2,0,2}.2.选A.在数轴上表示集合M,N,如图所示, 则M∪N={x|x<-5或x>-3}.3.选A.在数轴上表示集合S,T如图所示.因为S∪T=R,由数轴可得
解得-3
(1){x|x
(3){x|x
(2)注意当端点不在集合中时,应用“空心点”表示,当端点在集合中时,应用“实心点”表示.【类题·通】
求集合并集的方法
(1)两集合用列举法给出:①依定义,直接观察求并集;②借助维恩图写并集.
(2)两集合用描述法给出:①直接观察,写出并集;
②借助数轴,求出并集.(3)一个集合用描述法,另一个用列举法:①直接观察,找出并集;②借助图形,观察写出并集.
提醒:若两个集合中有相同元素,在求其并集时,只能算作一个.【习练·破】
1.满足条件{1,2}∪M={1,2,3}的所有集合M的个数是 ( )
A.1 B.2
C.3 D.4【解析】选D.因为{1,2}∪M={1,2,3},
所以3∈M,则满足条件的M可以是{3}或{1,3}或{2,3}或{1,2,3},共有4个.2.若集合A=(-∞,1],B=[0,+∞),则A∪B=_______.?【解析】如图所以A∪B=R.
答案:R【加练·固】
点集A={(x,y)|x<0},B={(x,y)|y<0},则A∪B中的元素不可能在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限【解析】选A.由题意得,A∪B中的元素是由横坐标小于0或纵坐标小于0的点构成的集合,所以A∪B中的元素不可能在第一象限.类型三 集合交、并运算的性质及综合应用
【典例】已知A={x|a≤x≤a+3},B={x|x<-1或x>5}.
世纪金榜导学号
(1)若A∩B=?,求实数a的取值范围.
(2)若A∪B=B,求实数a的取值范围.【思维·引】(1)根据A∩B=?列不等式组,求实数a的取值范围.
(2)由A∪B=B,推出A?B,列不等式求实数a的取值范围.【解析】(1)因为A∩B=?,所以
解得-1≤a≤2,所以实数a的取值范围是[-1,2].(2)因为A∪B=B,所以A?B,
所以a>5或a+3<-1,
即a的取值范围为a>5或a<-4,
所以实数a的取值范围是(-∞,-4)∪(5,+∞).【素养·探】
交集、并集运算性质的应用问题中,经常利用核心素养中的直观想象,常利用维恩图或数轴直观展示,根据集合运算结果分析集合之间的关系并列出不等式(组),求参数的值或范围.本例中若将条件改为A={x|-3
解得2≤k≤ .综合(1)(2)可知k的取值范围是【类题·通】
1.集合运算常用的性质
(1)A∪B=B?A?B.(2)A∩B=A?A?B.
(3)A∩B=A∪B?A=B.2.利用集合交集、并集的性质解题的方法及关注点
(1)方法:利用集合的交集、并集性质解题时,常常遇到A∪B=B,A∩B=A等问题,解答时常借助于交集、并集的定义及已知集合间的关系去转化为集合间的关系求解.(2)关注点:当集合A?B时,若集合A不确定,运算时要考虑A=?的情况,否则易漏解.【习练·破】
1.(2018·天津高考)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C=( )
A.{-1,1} B.{0,1}
C.{-1,0,1} D.{2,3,4}【解析】选C.因为集合A={1,2,3,4},
B={-1,0,2,3},A∪B={-1,0,1,2,3,4},
所以(A∪B)∩C={-1,0,1}.2. 集合A={x|x2-3x+2=0},B={x|x2-2x+a-1=0},A∩B=B,求a的取值范围.【解析】由题意,得A={1,2},因为A∩B=B,
当B=?时,(-2)2-4(a-1)<0,解得a>2;
当1∈B时,1-2+a-1=0,
解得a=2,且此时B={1},符合题意;当2∈B时,4-4+a-1=0,
解得a=1,此时B={0,2},不合题意;
当1∈B且2∈B时,此时a无解.综上所述,a的取值范围是[2,+∞).
