2020版新教材高中数学第一章集合与常用逻辑用语1.1.3.2补集及综合应用课件新人教B版必修1:90张PPT
文档属性
| 名称 | 2020版新教材高中数学第一章集合与常用逻辑用语1.1.3.2补集及综合应用课件新人教B版必修1:90张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览










文档简介
课件90张PPT。第2课时
补集及综合应用 1.全集的概念及符号表示
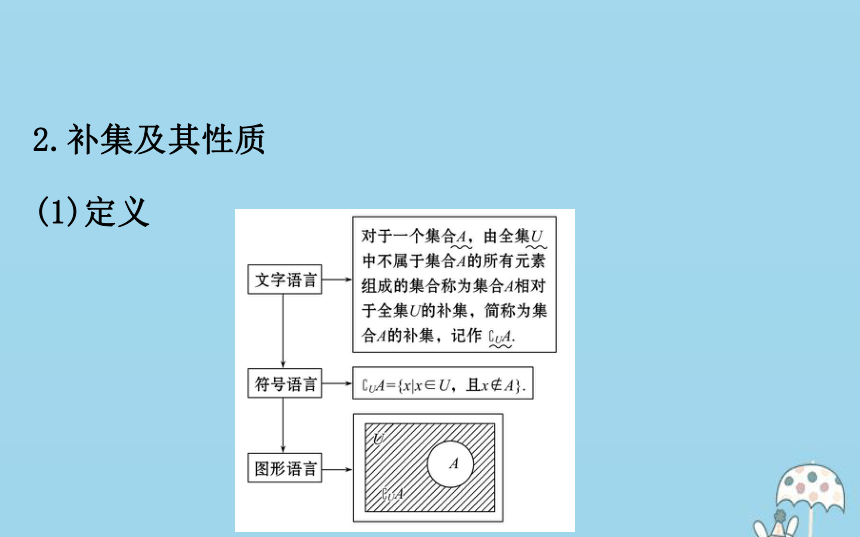
在研究集合与集合之间的关系时,如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集.全集通常用U表示.2.补集及其性质
(1)定义(2)性质:【思考】
?UA,A,U三者之间有什么关系?
提示:A?U,?UA?U,A∪(?UA)=U,A∩(?UA)=?.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)?UU=?,?U ?=U. ( )
(2)若A?B?U,则?UA??UB. ( )
(3)若x∈U,则x∈A或x∈?UA,二者必居其一. ( ) 提示:
(1)√.由集合补集的定义可知两个等式都成立.
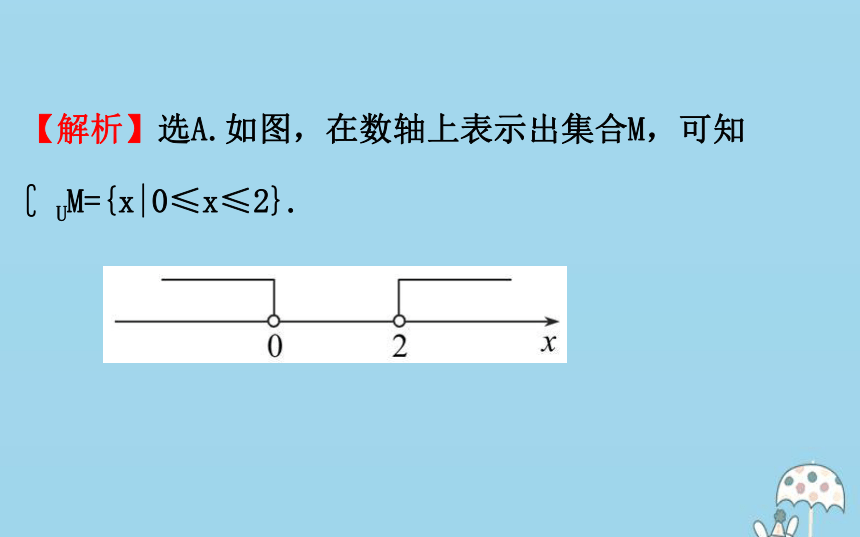
(2)√.画出维恩图可知,此说法正确.(3)√.根据补集的定义可知,此说法正确.2.设集合U=R,M={x|x>2或x<0},则?UM= ( )
A.{x|0≤x≤2} B.{x|0C.{x|x<0或x>2} D.{x|x≤0或x≥2}【解析】选A.如图,在数轴上表示出集合M,可知?UM={x|0≤x≤2}.3.已知全集U={x|-5【解析】易知U={-4,-3,-2,-1,0,1,2,3,4},
A={0,1,2},故?UA={-4,-3,-2,-1,3,4}.
答案:{-4,-3,-2,-1,3,4}类型一 补集的运算
【典例】1.(2018·浙江高考)已知全集U={1,2,3,4,5},A={1,3},则?UA= ( )
A.? B.{1,3}
C.{2,4,5} D.{1,2,3,4,5}2.若集合A=[-1,1),当S分别取下列集合时,求?SA.
(1)S=R.(2)S=(-∞,2].(3)S=[-4,1].【思维·引】
1.根据补集的定义直接写出.
2.画数轴表示集合S和集合A,观察数轴结合补集的定义求出?SA.【解析】1.选C.因为全集U={1,2,3,4,5},A={1,3},所以?UA={2,4,5}.2.(1)把集合A表示在数轴上如图所示.由图知?SA=(-∞,-1)∪[1,+∞).(2)把集合S和A表示在数轴上,如图所示.由图易知?SA=(-∞,-1)∪[1,2].(3)把集合S和A表示在数轴上,如图所示.由图知?SA=[-4,-1)∪{1}.【内化·悟】
借助数轴求集合的补集时要关注什么问题?
提示:(1)注意全集是什么.(2)端点的画法及取到与否.【类题·通】
求集合补集的依据及处理技巧
(1)依据:集合补集的定义.
(2)两种处理技巧:
①当集合用列举法表示时,可借助维恩图求解;②当集合是用描述法表示的连续数集时,可借助数轴,利用数轴分析求解.
【习练·破】
1.若全集U={0,1,2,3}且?UA ={2},则集合A的真子集共有 ( )
A.3个 B.5个 C.7个 D.8个【解析】选C.因为U={0,1,2,3}且?UA={2},
所以A={0,1,3},所以集合A的真子集共有7个.2.已知全集U=[-3,+∞),集合A=(-3,4],则?UA=________.?【解析】借助数轴得?UA={-3}∪(4,+∞).
答案:{-3}∪(4,+∞)【加练·固】
已知全集为U,集合A={1,3,5,7}, ?UA={2,4,6},?UB={1,4,6},求集合B.【解析】
方法一:因为A={1,3,5,7}, ?UA={2,4,6},
所以U={1,2,3,4,5,6,7}.
又?UB={1,4,6},所以B={2,3,5,7}.方法二:满足题意的维恩图如图所示.由图可知B={2,3,5,7}.类型二 集合交、并、补的综合运算
角度1 借助维恩图进行集合的基本运算
【典例】1.如图所示,I是全集,M,P,S是I的3个子集,则阴影部分所表示的集合是 ( )A.(M∩P)∩S B.(M∩P)∪S
C.(M∩P)∩?IS D.(M∩P)∪?IS2.若设全集U={1,2,3,4,5},A={1,2,5},B={2,4,5}.世纪金榜导学号
(1)计算?UA,?UB,A∪B,A∩B.
(2)计算(?UA)∪(?UB),(?UA)∩(?UB),?U(A∪B),?U(A∩B).【思维·引】
1.根据交、并、补集的定义,逐个检验.
2.进行集合的交、并、补混合运算时,有括号的先算括号内的,然后按照从左到右的顺序进行计算.【解析】1.选C.阴影部分是M与P的公共部分,且在S的外部.2.(1)因为U={1,2,3,4,5},A={1,2,5},
B={2,4,5},
所以?UA={3,4},?UB={1,3},
A∪B={1,2,4,5},A∩B={2,5}.
(2)(?UA)∪(?UB)={1,3,4},(?UA)∩(?UB)={3},
?U(A∪B)={3},?U(A∩B)={1,3,4}.【素养·探】
在集合交、并、补的综合运算问题中,经常利用核心素养中的直观想象,利用维恩图和数轴描述、分析集合的运算问题.
在本例2(2)的基础上,猜测一个一般性的结论,并利用维恩图证明.【解析】由此可猜测:(?UA)∪(?UB)=?U(A∩B);
(?UA)∩(?UB)=?U(A∪B).
证明如下:
用维恩图表示(?UA)∪(?UB)=?U(A∩B),有用维恩图表示(?UA)∩(?UB)=?U(A∪B)有:角度2 借助数轴进行集合的基本运算
【典例】1.(2018·天津高考)设全集为R,集合A={x|0A.{x|0C.{x|1≤x<2} D.{x|01.先计算?RB,再计算A∩(?RB).
2.画数轴,先计算A∩B,?UA,?UB,再计算(?UA)∪B,A∩(?UB).【解析】1.选B.因为集合B={x|x≥1},
所以?RB={x|x<1},所以A∩(?RB)={x|0所以?UA=(-∞,-2]∪[3,4],
?UB=(-∞,-3)∪(2,4].
A∩B=(-2,2],
所以(?UA)∪B=(-∞,2]∪[3,4],
A∩(?UB)=(2,3). 【类题·通】
求集合交、并、补运算的方法【习练·破】
1.全集U={x|x<10,x∈N*},A?U,B?U,(?UB)∩A={1,9},A∩B={3},(?UA)∩(?UB)={4,6,7},求集合A,B.【解析】方法一:根据题意作出维恩图如图所示. 由图可知A={1,3,9},B={2,3,5,8}. 方法二:因为(?UB)∩A={1,9},
(?UA)∩(?UB)={4,6,7},所以?UB={1,4,6,7,9}.
又因为U={1,2,3,4,5,6,7,8,9},所以B={2,3,5,8}.
因为(?UB)∩A={1,9},A∩B={3},所以A={1,3,9}. 2.已知全集U=[-1,4],A=[-1,1],B=(0,3],求?UA,(?UB)∩A.【解析】因为U=[-1,4],A=[-1,1],
B=(0,3],结合数轴(如图).可知?UA=(1,4],
?UB=(3,4]∪[-1,0].结合数轴(如图).可知(?UB)∩A=[-1,0].【加练·固】已知全集U=R,A={x|-4≤x<2},B=
{x|-1所以A∩B={x|-13}.
又P=所以(?UB)∪P= .
又?UP=
所以(A∩B)∩(?UP)
={x|-1【典例】1.已知全集U={2,0,3-a2},P={2,a2-a-2},
且?UP={-1},则实数a的值为________.2.已知集合A=[2,+∞),B=[-1,5]. 世纪金榜导学号
(1)求(?RA)∩B.
(2)若D=[1-a,1+a],且D∪(?RB)=?RB,求实数a的取值范围.【思维·引】1.由?UP={-1}得,-1∈U,且-1?P,0∈P,列方程求a的值.
2.(1)先计算?RA,再计算(?RA)∩B.
(2)由D∪(?RB)=?RB,确定D与?RB的关系.【解析】1.因为?UP={-1},所以-1∈U,且-1?P,0∈P.
所以 解得a=2.
经检验,a=2符合题意,故实数a的值为2.
答案:22.(1)因为集合A=[2,+∞),B=[-1,5].
所以?RA=(-∞,2),(?RA)∩B=[-1,2).
(2)因为D=[1-a,1+a]且D∪(?RB)=?RB,
?RB=(-∞,-1)∪(5,+∞),所以D??RB,
当D=?时,1-a>1+a,解得a<0,成立;当D≠?时, 或 ,无解.
综上,实数a的取值范围是(-∞,0).【内化·悟】
对于含有参数的交、并、补问题,依据题目条件求出参数值后,还要注意什么问题?
提示:需将参数值代回检验,舍去不符合题意的参数值.【类题·通】
由集合的补集求解参数的方法
(1)有限集:由补集求参数问题,若集合中元素个数有限时,可利用补集定义并结合集合知识求解.(2)无限集:与集合交、并、补运算有关的求参数问题,若集合中元素有无限个时,一般借助数轴分析法求解.【发散·拓】补集思想的应用
对于一些比较复杂、比较抽象、条件和结论之间关系不明确、难于从正面入手的数学问题,在解题时,可从问题的反面入手,探求已知和未知的关系,这时能化难为易,化隐为显,从而将问题解决.这就是“正难则反”的解题策略,也是处理问题的间接化原则的体现.【延伸·练】
已知集合A={x|x2+ax+1=0},B={x|x2+2x-a=0},C={x|x2+2ax+2=0}.若三个集合至少有一个集合不是空集,求实数a的取值范围. 【解析】假设三个方程均无实根,则有
即 解得-三个方程至少有一个方程有实根,即三个集合至少有
一个集合不是空集.
则a的取值范围为【习练·破】
已知集合A=(-∞,a),B=(-∞,1)∪(3,+∞).
若A∩(?RB)=?,求实数a的取值范围.【解析】?RB=[1,3],利用数轴画出集合A与?RB,如图.因为A∩(?RB)=?,所以应满足a≤1,故a的取值范围是(-∞,1].【加练·固】
已知全集U=[-6,5],M=(-3,2],N=(0,2).
(1)求M∩(?UN).
(2)若C=[a,2a-1]且C?(?UM),求a的取值范围.【解析】(1)全集U=[-6,5],
M=(-3,2],
N=(0,2),
所以?UN=[-6,0]∪[2,5],
所以M∩(?UN)=(-3,0]∪{2}.(2)因为C=[a,2a-1],?UM=[-6,-3]∪(2,5],且C?(?UM),
当C=?时,a>2a-1,解得a<1;
当C≠?且C?(?UM)时, 或
解得2综上所述:a的取值范围是(-∞,1)∪(2,3].类型四 集合的基本运算在实际问题中的应用
【生活情境】
某校随机抽取50名学生调查对A,B两事件的态度,有
如下结果:赞成A的人数是这50名学生的 ,其余的
不赞成;赞成B的比赞成A的多3人,其余的不赞成;另
外,对A,B都不赞成的学生数比对A,B都赞成的学生数的 多1人.你能说出对A,B都赞成的学生和都不赞成的学生各有多少人吗?
【转化模板】
1. ——由题意,A和B都赞成对应交集、A和B都不赞
成对应并集的补集,所以可建立集合模型求解.
2. ——设50名学生组成的集合为U,赞成A的学生全
体为集合A,赞成B的学生全体为集合B.3. ——已知全集U中有50个元素,集合A中的元素个
数是全集的 ,集合B中的元素比集合A中的元素多
3个,集合A∪B相对于全集U的补集的元素个数比集合
A∩B的元素的个数的 多1人.求集合A和集合B元素的
个数.4. ——设对A,B都赞成的学生人数为x.已知赞成A
的人数为50× =30,赞成B的人数为30+3=33, 记
50名学生组成的集合为U,赞成A的学生全体为集合A,
赞成B的学生全体为集合B.用维恩图表示如图所示.已知对A,B都赞成的学生人数为x,
则对A,B都不赞成的学生人数为 +1,
赞成A而不赞成B的人数为30-x,
赞成B而不赞成A的人数为33-x.
依题意(30-x)+(33-x)+x+ =50,解得x=21.5. ——对A,B都赞成的学生有21人,都不赞成的有
8人.
补集及综合应用 1.全集的概念及符号表示
在研究集合与集合之间的关系时,如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集.全集通常用U表示.2.补集及其性质
(1)定义(2)性质:【思考】
?UA,A,U三者之间有什么关系?
提示:A?U,?UA?U,A∪(?UA)=U,A∩(?UA)=?.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)?UU=?,?U ?=U. ( )
(2)若A?B?U,则?UA??UB. ( )
(3)若x∈U,则x∈A或x∈?UA,二者必居其一. ( ) 提示:
(1)√.由集合补集的定义可知两个等式都成立.
(2)√.画出维恩图可知,此说法正确.(3)√.根据补集的定义可知,此说法正确.2.设集合U=R,M={x|x>2或x<0},则?UM= ( )
A.{x|0≤x≤2} B.{x|0
A={0,1,2},故?UA={-4,-3,-2,-1,3,4}.
答案:{-4,-3,-2,-1,3,4}类型一 补集的运算
【典例】1.(2018·浙江高考)已知全集U={1,2,3,4,5},A={1,3},则?UA= ( )
A.? B.{1,3}
C.{2,4,5} D.{1,2,3,4,5}2.若集合A=[-1,1),当S分别取下列集合时,求?SA.
(1)S=R.(2)S=(-∞,2].(3)S=[-4,1].【思维·引】
1.根据补集的定义直接写出.
2.画数轴表示集合S和集合A,观察数轴结合补集的定义求出?SA.【解析】1.选C.因为全集U={1,2,3,4,5},A={1,3},所以?UA={2,4,5}.2.(1)把集合A表示在数轴上如图所示.由图知?SA=(-∞,-1)∪[1,+∞).(2)把集合S和A表示在数轴上,如图所示.由图易知?SA=(-∞,-1)∪[1,2].(3)把集合S和A表示在数轴上,如图所示.由图知?SA=[-4,-1)∪{1}.【内化·悟】
借助数轴求集合的补集时要关注什么问题?
提示:(1)注意全集是什么.(2)端点的画法及取到与否.【类题·通】
求集合补集的依据及处理技巧
(1)依据:集合补集的定义.
(2)两种处理技巧:
①当集合用列举法表示时,可借助维恩图求解;②当集合是用描述法表示的连续数集时,可借助数轴,利用数轴分析求解.
【习练·破】
1.若全集U={0,1,2,3}且?UA ={2},则集合A的真子集共有 ( )
A.3个 B.5个 C.7个 D.8个【解析】选C.因为U={0,1,2,3}且?UA={2},
所以A={0,1,3},所以集合A的真子集共有7个.2.已知全集U=[-3,+∞),集合A=(-3,4],则?UA=________.?【解析】借助数轴得?UA={-3}∪(4,+∞).
答案:{-3}∪(4,+∞)【加练·固】
已知全集为U,集合A={1,3,5,7}, ?UA={2,4,6},?UB={1,4,6},求集合B.【解析】
方法一:因为A={1,3,5,7}, ?UA={2,4,6},
所以U={1,2,3,4,5,6,7}.
又?UB={1,4,6},所以B={2,3,5,7}.方法二:满足题意的维恩图如图所示.由图可知B={2,3,5,7}.类型二 集合交、并、补的综合运算
角度1 借助维恩图进行集合的基本运算
【典例】1.如图所示,I是全集,M,P,S是I的3个子集,则阴影部分所表示的集合是 ( )A.(M∩P)∩S B.(M∩P)∪S
C.(M∩P)∩?IS D.(M∩P)∪?IS2.若设全集U={1,2,3,4,5},A={1,2,5},B={2,4,5}.世纪金榜导学号
(1)计算?UA,?UB,A∪B,A∩B.
(2)计算(?UA)∪(?UB),(?UA)∩(?UB),?U(A∪B),?U(A∩B).【思维·引】
1.根据交、并、补集的定义,逐个检验.
2.进行集合的交、并、补混合运算时,有括号的先算括号内的,然后按照从左到右的顺序进行计算.【解析】1.选C.阴影部分是M与P的公共部分,且在S的外部.2.(1)因为U={1,2,3,4,5},A={1,2,5},
B={2,4,5},
所以?UA={3,4},?UB={1,3},
A∪B={1,2,4,5},A∩B={2,5}.
(2)(?UA)∪(?UB)={1,3,4},(?UA)∩(?UB)={3},
?U(A∪B)={3},?U(A∩B)={1,3,4}.【素养·探】
在集合交、并、补的综合运算问题中,经常利用核心素养中的直观想象,利用维恩图和数轴描述、分析集合的运算问题.
在本例2(2)的基础上,猜测一个一般性的结论,并利用维恩图证明.【解析】由此可猜测:(?UA)∪(?UB)=?U(A∩B);
(?UA)∩(?UB)=?U(A∪B).
证明如下:
用维恩图表示(?UA)∪(?UB)=?U(A∩B),有用维恩图表示(?UA)∩(?UB)=?U(A∪B)有:角度2 借助数轴进行集合的基本运算
【典例】1.(2018·天津高考)设全集为R,集合A={x|0
2.画数轴,先计算A∩B,?UA,?UB,再计算(?UA)∪B,A∩(?UB).【解析】1.选B.因为集合B={x|x≥1},
所以?RB={x|x<1},所以A∩(?RB)={x|0
?UB=(-∞,-3)∪(2,4].
A∩B=(-2,2],
所以(?UA)∪B=(-∞,2]∪[3,4],
A∩(?UB)=(2,3). 【类题·通】
求集合交、并、补运算的方法【习练·破】
1.全集U={x|x<10,x∈N*},A?U,B?U,(?UB)∩A={1,9},A∩B={3},(?UA)∩(?UB)={4,6,7},求集合A,B.【解析】方法一:根据题意作出维恩图如图所示. 由图可知A={1,3,9},B={2,3,5,8}. 方法二:因为(?UB)∩A={1,9},
(?UA)∩(?UB)={4,6,7},所以?UB={1,4,6,7,9}.
又因为U={1,2,3,4,5,6,7,8,9},所以B={2,3,5,8}.
因为(?UB)∩A={1,9},A∩B={3},所以A={1,3,9}. 2.已知全集U=[-1,4],A=[-1,1],B=(0,3],求?UA,(?UB)∩A.【解析】因为U=[-1,4],A=[-1,1],
B=(0,3],结合数轴(如图).可知?UA=(1,4],
?UB=(3,4]∪[-1,0].结合数轴(如图).可知(?UB)∩A=[-1,0].【加练·固】已知全集U=R,A={x|-4≤x<2},B=
{x|-1
又P=所以(?UB)∪P= .
又?UP=
所以(A∩B)∩(?UP)
={x|-1
且?UP={-1},则实数a的值为________.2.已知集合A=[2,+∞),B=[-1,5]. 世纪金榜导学号
(1)求(?RA)∩B.
(2)若D=[1-a,1+a],且D∪(?RB)=?RB,求实数a的取值范围.【思维·引】1.由?UP={-1}得,-1∈U,且-1?P,0∈P,列方程求a的值.
2.(1)先计算?RA,再计算(?RA)∩B.
(2)由D∪(?RB)=?RB,确定D与?RB的关系.【解析】1.因为?UP={-1},所以-1∈U,且-1?P,0∈P.
所以 解得a=2.
经检验,a=2符合题意,故实数a的值为2.
答案:22.(1)因为集合A=[2,+∞),B=[-1,5].
所以?RA=(-∞,2),(?RA)∩B=[-1,2).
(2)因为D=[1-a,1+a]且D∪(?RB)=?RB,
?RB=(-∞,-1)∪(5,+∞),所以D??RB,
当D=?时,1-a>1+a,解得a<0,成立;当D≠?时, 或 ,无解.
综上,实数a的取值范围是(-∞,0).【内化·悟】
对于含有参数的交、并、补问题,依据题目条件求出参数值后,还要注意什么问题?
提示:需将参数值代回检验,舍去不符合题意的参数值.【类题·通】
由集合的补集求解参数的方法
(1)有限集:由补集求参数问题,若集合中元素个数有限时,可利用补集定义并结合集合知识求解.(2)无限集:与集合交、并、补运算有关的求参数问题,若集合中元素有无限个时,一般借助数轴分析法求解.【发散·拓】补集思想的应用
对于一些比较复杂、比较抽象、条件和结论之间关系不明确、难于从正面入手的数学问题,在解题时,可从问题的反面入手,探求已知和未知的关系,这时能化难为易,化隐为显,从而将问题解决.这就是“正难则反”的解题策略,也是处理问题的间接化原则的体现.【延伸·练】
已知集合A={x|x2+ax+1=0},B={x|x2+2x-a=0},C={x|x2+2ax+2=0}.若三个集合至少有一个集合不是空集,求实数a的取值范围. 【解析】假设三个方程均无实根,则有
即 解得-
一个集合不是空集.
则a的取值范围为【习练·破】
已知集合A=(-∞,a),B=(-∞,1)∪(3,+∞).
若A∩(?RB)=?,求实数a的取值范围.【解析】?RB=[1,3],利用数轴画出集合A与?RB,如图.因为A∩(?RB)=?,所以应满足a≤1,故a的取值范围是(-∞,1].【加练·固】
已知全集U=[-6,5],M=(-3,2],N=(0,2).
(1)求M∩(?UN).
(2)若C=[a,2a-1]且C?(?UM),求a的取值范围.【解析】(1)全集U=[-6,5],
M=(-3,2],
N=(0,2),
所以?UN=[-6,0]∪[2,5],
所以M∩(?UN)=(-3,0]∪{2}.(2)因为C=[a,2a-1],?UM=[-6,-3]∪(2,5],且C?(?UM),
当C=?时,a>2a-1,解得a<1;
当C≠?且C?(?UM)时, 或
解得2
【生活情境】
某校随机抽取50名学生调查对A,B两事件的态度,有
如下结果:赞成A的人数是这50名学生的 ,其余的
不赞成;赞成B的比赞成A的多3人,其余的不赞成;另
外,对A,B都不赞成的学生数比对A,B都赞成的学生数的 多1人.你能说出对A,B都赞成的学生和都不赞成的学生各有多少人吗?
【转化模板】
1. ——由题意,A和B都赞成对应交集、A和B都不赞
成对应并集的补集,所以可建立集合模型求解.
2. ——设50名学生组成的集合为U,赞成A的学生全
体为集合A,赞成B的学生全体为集合B.3. ——已知全集U中有50个元素,集合A中的元素个
数是全集的 ,集合B中的元素比集合A中的元素多
3个,集合A∪B相对于全集U的补集的元素个数比集合
A∩B的元素的个数的 多1人.求集合A和集合B元素的
个数.4. ——设对A,B都赞成的学生人数为x.已知赞成A
的人数为50× =30,赞成B的人数为30+3=33, 记
50名学生组成的集合为U,赞成A的学生全体为集合A,
赞成B的学生全体为集合B.用维恩图表示如图所示.已知对A,B都赞成的学生人数为x,
则对A,B都不赞成的学生人数为 +1,
赞成A而不赞成B的人数为30-x,
赞成B而不赞成A的人数为33-x.
依题意(30-x)+(33-x)+x+ =50,解得x=21.5. ——对A,B都赞成的学生有21人,都不赞成的有
8人.
