2020版新教材高中数学第一章集合与常用逻辑用语1.2.3.2充要条件课件新人教B版必修1:62张PPT
文档属性
| 名称 | 2020版新教材高中数学第一章集合与常用逻辑用语1.2.3.2充要条件课件新人教B版必修1:62张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览











文档简介
课件62张PPT。第2课时
充 要 条 件 1.充要条件【思考】
符号“?”的含义是什么?
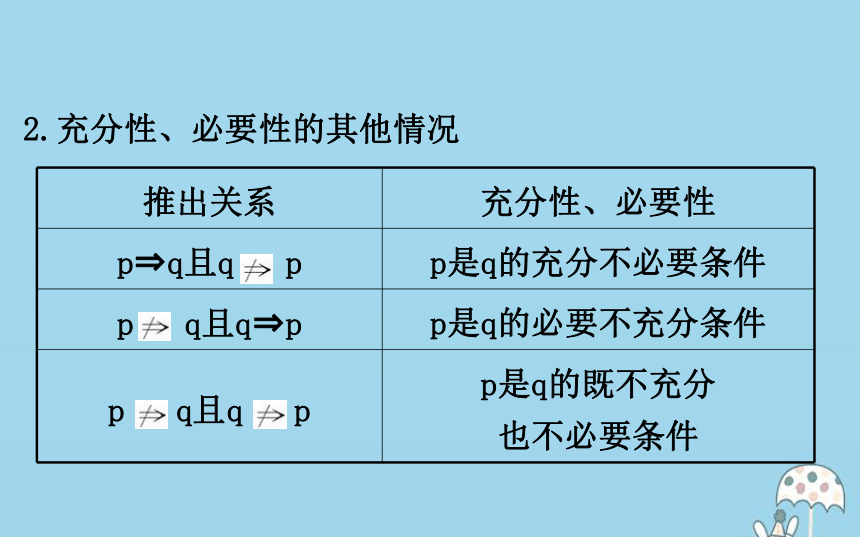
提示:“?”表示“等价”,如“A与B等价”指的是“如果A,那么B”,同时有“如果B,那么A”,或者说“从A推出B”,同时可“从B推出A”.2.充分性、必要性的其他情况【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)当p是q的充要条件时,也可说成q成立当且仅当
p成立. ( )
(2)若p q和q p有一个成立,则p一定不是q的
充要条件. ( )(3)若p是q的充要条件,q是r的充要条件,则p是r的充要条件. ( )提示:(1)√.当p是q的充要条件时,p?q,且q?p,
故说成q成立当且仅当p成立,这种说法正确.
(2)√.若p q或q p,则p不是q的充分条件,
或p不是q的必要条件,故此说法正确.
(3)√.因为p?q,q?r,所以p?r,所以p是r的充
要条件.2.“a+b<0”是“a<0,b<0”的 ( )
A.充分不必要条件
B.充要条件
C.必要不充分条件
D.既不充分也不必要条件【解析】选C.当a与b异号且负数绝对值大时,也有
a+b<0,所以“a+b<0” “a<0,b<0”,
显然“a<0,b<0”?“a+b<0”,所以“a+b<0”
是“a<0,b<0”的必要不充分条件.3.点P(x,y)是第二象限的点的充要条件是 ( )
A.x<0,y<0 B.x<0,y>0
C.x>0,y>0 D.x>0,y<0
【解析】选B.第二象限的点横坐标小于0,纵坐标大于0,所以点P(x,y)是第二象限的点的充要条件是x<0,y>0.类型一 充分条件和必要条件的综合判断
【典例】1.“b2=ac”是“ = 成立”的( )
A.充分不必要条件
B.充要条件
C.必要不充分条件
D.既不充分也不必要条件2.下列各题中,p是q的什么条件(“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”)? 世纪金榜导学号
(1)p:x≠0,q:x+|x|>0.
(2)p:a>0,q:关于x的方程ax+b=0(a,b∈R)有唯一解.(3)p:ab>0,a,b∈R,q:|a+b|=|a|+|b|.
(4)p:c=0,q:y=ax2+bx+c(a≠0)的图象经过原点.【思维·引】1.依据等式两边同乘以非零实数,等式仍成立判断.
2.依据“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”的定义判断.【解析】1.选C.b2=ac = ,如b=0,c=0时,b2=ac,而 , 无意义.但 = ?b2=ac,
所以“b2=ac”是“ = ”的必要不充分条件.2.(1)因为由x≠0推不出x+|x|>0,如x=-1≠0,
但是x+|x|=0,所以p q,
由x+|x|>0可得x>0,可推出x≠0,所以q?p,
所以p是q的必要不充分条件.(2)当a>0时,关于x的方程ax+b=0(a,b∈R)有唯一
解x=- ,所以p?q,
若关于x的方程ax+b=0(a,b∈R)有唯一解,则a≠0,
推不出a>0,所以q p,
所以p是q的充分不必要条件.(3)当ab>0时,|a+b|=|a|+|b|成立,所以p?q,因为a=0时,也有|a+b|=|a|+|b|,
所以q p,所以p是q的充分不必要条件.(4)当c=0时,函数y=ax2+bx的图象经过原点;
当y=ax2+bx+c(a≠0)的图象经过原点时,
0=a×02+b×0+c,所以c=0,
所以p?q,所以p是q的充要条件.【内化·悟】
根据充分必要条件的定义和判断方法,你能总结一个记忆口诀吗?
提示:顺向为充(即若p?q,则p是q的充分条件),逆向为必(即若p?q,则q是p的必要条件).【类题·通】
从命题角度判断p是q的充分必要条件
(1)原理:
判断p是q的充分必要条件,主要是判断p?q及q?p这两个命题是否成立.(2)方法:
①若p?q成立,则p是q的充分条件,同时q是p的必要条件;
②若q?p成立,则p是q的必要条件,同时q是p的充分条件;
③若二者都成立,则p与q互为充要条件.【习练·破】
下列各题中,p是q的什么条件(“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”)?(1)p:x2=3x+4,q:x= .
(2)p:a是自然数,q:a是正数.
(3)p:a=1,q:a的倒数是其本身.
(4)p:点P(2-a,3a-2)到两坐标轴距离相等,q:a=1或a=0.【解析】(1)当x=-1时,x2=3x+4成立,但是x=
不成立,所以p q,由x= 两边平方可得
x2=3x+4,所以q?p,所以p是q的必要不充分条件.
(2)0是自然数,但是0不是正数,
所以p q,1.5是正数,但是1.5不是自然数,
所以q p,所以p是q的既不充分也不必要条件.(3)倒数是其本身的数有±1,所以q p,且p?q,
所以p是q的充分不必要条件.(4)当a=1,点P(1,1)到两坐标轴距离相等;
当a=0,点P(2,-2)到两坐标轴距离相等;
当点P(2-a,3a-2)到两坐标轴距离相等时,
|2-a|=|3a-2|,解得a=1或a=0.
所以p?q,所以p是q的充要条件.【加练·固】
下列各题中,p是q的什么条件(“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”)?(1)p:x=y,q:
(2)p:∠1=∠2,q:∠1与∠2是对顶角.
(3)p:反比例函数y= 的图象在第二、四象限,
q:m<5.
(4)p:a>1,q:a> .【解析】(1)当a=0时,x=y
?x=y,所以p是q的必要不充分条件.
(2)对顶角相等,但相等的角不一定是对顶角,
所以p q,且q?p,所以p是q的必要不充分条件.(3)反比例函数y= 的图象在第二、四象限?
m-5<0?m<5,所以p是q的充要条件.
(4)当a>1时,
所以a> ,所以p?q,
当a=- 时,a> ,所以q p,
所以p是q的充分不必要条件.类型二 充要条件的证明
【典例】已知关于x的方程ax2+bx+c=0(※),判断a+b+c=0是否是方程(※)有一个根为1的充要条件. 世纪金榜导学号
【思维·引】从充分性和必要性两个方面进行证明.【证明】因为a+b+c=0,
所以c=-a-b,代入方程ax2+bx+c=0中,
得ax2+bx-a-b=0,即(x-1)(ax+a+b)=0.
所以方程(※)有一个根为1,
所以a+b+c=0?方程(※)有一个根为1,因为方程ax2+bx+c=0有一个根为1,
所以x=1满足方程ax2+bx+c=0.
所以有a×12+b×1+c=0,即a+b+c=0.
所以方程(※)有一个根为1?a+b+c=0,
从而a+b+c=0?方程(※)有一个根为1,
因此a+b+c=0是方程(※)有一个根为1的充要条件.【素养·探】
在与充要条件的证明有关的问题中,经常利用核心
素养中的逻辑推理,通过命题真假的证明,判断充
分、必要条件,提高分析、推理、论证的能力.
将本例的条件“有一个根为1”改为“有一个正根和一
个负根”,“a+b+c=0”改为“ac<0”,如何判断?【证明】因为ac<0,所以Δ=b2-4ac>0,方程ax2+bx+c=0中有两个不等实根,由根与系数关系
可知这两个根的积为 <0,
所以方程ax2+bx+c=0有一个正根和一个负根,
所以ac<0?方程(※)有一个正根和一个负根,因为方程ax2+bx+c=0有一个正根和一个负根,
由根与系数关系可知这两个根的积为 <0,
所以ac<0.所以方程(※)有一个正根和一个负根?
ac<0,从而ac<0?方程(※)有一个正根和一个负
根,因此ac<0是方程(※)有一个正根和一个负根的
充要条件.【类题·通】
充要条件的证明策略
(1)要证明一个条件p是否是q的充要条件,需要从充分性和必要性两个方向进行,即证明两个命题“若p,则q”为真且“若q,则p”为真.(2)在证明的过程中也可以转化为集合的思想来证明,证明p与q的解集是相同的,证明前必须分清楚充分性和必要性,即搞清楚由哪些条件推证到哪些结论.
提醒:证明时一定要注意,分清充分性与必要性的证明方向.【习练·破】
已知x,y都是非零实数,且x>y,判断xy>0是否是
的充要条件.【证明】由xy>0及x>y,得
所以xy>0?
即 <0,
又由x>y,得y-x<0,所以xy>0.
所以 ?xy>0,从而xy>0? ,
所以xy>0是 的充要条件.【加练·固】
求关于x的方程ax2+x+1=0至少有一个负实根的充要条件.【解析】①当a=0时,解得x=-1,满足条件;
②当a≠0时,显然方程没有零根,若方程有两异号实根,则a<0;
若方程有两个负的实根,
则必须满足 综上,若方程至少有一个负的实根,则a≤ .
反之,若a≤ ,则方程至少有一个负的实根.
因此,关于x的方程ax2+x+1=0至少有一个负实根的充
要条件是a≤ .类型三 用集合观点解充分条件、必要条件问题
【典例】1.已知p:点M(1-a,2a+6)在第四象限,
q:a<1,则p是q的 ( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件2.已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围. 世纪金榜导学号【思维·引】1.第四象限内的点横坐标大于0,纵坐标小于0.依据“小范围”推“大范围”,“大范围”推不出“小范围”判断;
2.先把p,q等价转化,利用充分条件、必要条件、充要条件与集合间的包含关系,建立关于m的不等式(组)进行求解.【解析】1.选A.因为点M(1-a,2a+6)在第四象限,
所以 解得a<-3.
因为(-∞,-3) (-∞,1),
所以p?q,q p,
所以p是q的充分不必要条件.2.p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的必要不充分条件,
所以q是p的充分不必要条件,
即[1-m,1+m] [-2,10],
故有 解得m≤3.
又m>0,所以实数m的取值范围为(0,3].【素养·探】
在与用集合观点解充分条件、必要条件问题中,经常
利用核心素养中的直观想象,通过研究充分条件和必
要条件与集合关系,培养借助集合解决问题的能力.
将本例2的“p是q的必要不充分条件”改为“p是q的充
分不必要条件”,其他条件不变,求实数m的取值范围.【解析】p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的充分不必要条件,
设p代表的集合为A,q代表的集合为B,
所以A B.
所以 解不等式组得m>9或m≥9,
所以m≥9,
即实数m的取值范围是[9,+∞).【类题·通】
从集合的角度判断充分条件、必要条件和充要条件其中p:A={x|p(x)成立},q:B={x|q(x)成立}.【习练·破】
设p:实数x满足a0),q:实数x满足2所以q对应的集合是p对应集合的真子集,
所以(2,5] (a,4a)则 得 得即实数a的取值范围是 【加练·固】
已知p:-1所以p对应的集合是q对应集合的真子集,
所以(-1,3) [k-2,k+5],
所以
?-2≤k≤1.
所以实数k的取值范围是[-2,1].
充 要 条 件 1.充要条件【思考】
符号“?”的含义是什么?
提示:“?”表示“等价”,如“A与B等价”指的是“如果A,那么B”,同时有“如果B,那么A”,或者说“从A推出B”,同时可“从B推出A”.2.充分性、必要性的其他情况【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)当p是q的充要条件时,也可说成q成立当且仅当
p成立. ( )
(2)若p q和q p有一个成立,则p一定不是q的
充要条件. ( )(3)若p是q的充要条件,q是r的充要条件,则p是r的充要条件. ( )提示:(1)√.当p是q的充要条件时,p?q,且q?p,
故说成q成立当且仅当p成立,这种说法正确.
(2)√.若p q或q p,则p不是q的充分条件,
或p不是q的必要条件,故此说法正确.
(3)√.因为p?q,q?r,所以p?r,所以p是r的充
要条件.2.“a+b<0”是“a<0,b<0”的 ( )
A.充分不必要条件
B.充要条件
C.必要不充分条件
D.既不充分也不必要条件【解析】选C.当a与b异号且负数绝对值大时,也有
a+b<0,所以“a+b<0” “a<0,b<0”,
显然“a<0,b<0”?“a+b<0”,所以“a+b<0”
是“a<0,b<0”的必要不充分条件.3.点P(x,y)是第二象限的点的充要条件是 ( )
A.x<0,y<0 B.x<0,y>0
C.x>0,y>0 D.x>0,y<0
【解析】选B.第二象限的点横坐标小于0,纵坐标大于0,所以点P(x,y)是第二象限的点的充要条件是x<0,y>0.类型一 充分条件和必要条件的综合判断
【典例】1.“b2=ac”是“ = 成立”的( )
A.充分不必要条件
B.充要条件
C.必要不充分条件
D.既不充分也不必要条件2.下列各题中,p是q的什么条件(“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”)? 世纪金榜导学号
(1)p:x≠0,q:x+|x|>0.
(2)p:a>0,q:关于x的方程ax+b=0(a,b∈R)有唯一解.(3)p:ab>0,a,b∈R,q:|a+b|=|a|+|b|.
(4)p:c=0,q:y=ax2+bx+c(a≠0)的图象经过原点.【思维·引】1.依据等式两边同乘以非零实数,等式仍成立判断.
2.依据“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”的定义判断.【解析】1.选C.b2=ac = ,如b=0,c=0时,b2=ac,而 , 无意义.但 = ?b2=ac,
所以“b2=ac”是“ = ”的必要不充分条件.2.(1)因为由x≠0推不出x+|x|>0,如x=-1≠0,
但是x+|x|=0,所以p q,
由x+|x|>0可得x>0,可推出x≠0,所以q?p,
所以p是q的必要不充分条件.(2)当a>0时,关于x的方程ax+b=0(a,b∈R)有唯一
解x=- ,所以p?q,
若关于x的方程ax+b=0(a,b∈R)有唯一解,则a≠0,
推不出a>0,所以q p,
所以p是q的充分不必要条件.(3)当ab>0时,|a+b|=|a|+|b|成立,所以p?q,因为a=0时,也有|a+b|=|a|+|b|,
所以q p,所以p是q的充分不必要条件.(4)当c=0时,函数y=ax2+bx的图象经过原点;
当y=ax2+bx+c(a≠0)的图象经过原点时,
0=a×02+b×0+c,所以c=0,
所以p?q,所以p是q的充要条件.【内化·悟】
根据充分必要条件的定义和判断方法,你能总结一个记忆口诀吗?
提示:顺向为充(即若p?q,则p是q的充分条件),逆向为必(即若p?q,则q是p的必要条件).【类题·通】
从命题角度判断p是q的充分必要条件
(1)原理:
判断p是q的充分必要条件,主要是判断p?q及q?p这两个命题是否成立.(2)方法:
①若p?q成立,则p是q的充分条件,同时q是p的必要条件;
②若q?p成立,则p是q的必要条件,同时q是p的充分条件;
③若二者都成立,则p与q互为充要条件.【习练·破】
下列各题中,p是q的什么条件(“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”)?(1)p:x2=3x+4,q:x= .
(2)p:a是自然数,q:a是正数.
(3)p:a=1,q:a的倒数是其本身.
(4)p:点P(2-a,3a-2)到两坐标轴距离相等,q:a=1或a=0.【解析】(1)当x=-1时,x2=3x+4成立,但是x=
不成立,所以p q,由x= 两边平方可得
x2=3x+4,所以q?p,所以p是q的必要不充分条件.
(2)0是自然数,但是0不是正数,
所以p q,1.5是正数,但是1.5不是自然数,
所以q p,所以p是q的既不充分也不必要条件.(3)倒数是其本身的数有±1,所以q p,且p?q,
所以p是q的充分不必要条件.(4)当a=1,点P(1,1)到两坐标轴距离相等;
当a=0,点P(2,-2)到两坐标轴距离相等;
当点P(2-a,3a-2)到两坐标轴距离相等时,
|2-a|=|3a-2|,解得a=1或a=0.
所以p?q,所以p是q的充要条件.【加练·固】
下列各题中,p是q的什么条件(“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”)?(1)p:x=y,q:
(2)p:∠1=∠2,q:∠1与∠2是对顶角.
(3)p:反比例函数y= 的图象在第二、四象限,
q:m<5.
(4)p:a>1,q:a> .【解析】(1)当a=0时,x=y
?x=y,所以p是q的必要不充分条件.
(2)对顶角相等,但相等的角不一定是对顶角,
所以p q,且q?p,所以p是q的必要不充分条件.(3)反比例函数y= 的图象在第二、四象限?
m-5<0?m<5,所以p是q的充要条件.
(4)当a>1时,
所以a> ,所以p?q,
当a=- 时,a> ,所以q p,
所以p是q的充分不必要条件.类型二 充要条件的证明
【典例】已知关于x的方程ax2+bx+c=0(※),判断a+b+c=0是否是方程(※)有一个根为1的充要条件. 世纪金榜导学号
【思维·引】从充分性和必要性两个方面进行证明.【证明】因为a+b+c=0,
所以c=-a-b,代入方程ax2+bx+c=0中,
得ax2+bx-a-b=0,即(x-1)(ax+a+b)=0.
所以方程(※)有一个根为1,
所以a+b+c=0?方程(※)有一个根为1,因为方程ax2+bx+c=0有一个根为1,
所以x=1满足方程ax2+bx+c=0.
所以有a×12+b×1+c=0,即a+b+c=0.
所以方程(※)有一个根为1?a+b+c=0,
从而a+b+c=0?方程(※)有一个根为1,
因此a+b+c=0是方程(※)有一个根为1的充要条件.【素养·探】
在与充要条件的证明有关的问题中,经常利用核心
素养中的逻辑推理,通过命题真假的证明,判断充
分、必要条件,提高分析、推理、论证的能力.
将本例的条件“有一个根为1”改为“有一个正根和一
个负根”,“a+b+c=0”改为“ac<0”,如何判断?【证明】因为ac<0,所以Δ=b2-4ac>0,方程ax2+bx+c=0中有两个不等实根,由根与系数关系
可知这两个根的积为 <0,
所以方程ax2+bx+c=0有一个正根和一个负根,
所以ac<0?方程(※)有一个正根和一个负根,因为方程ax2+bx+c=0有一个正根和一个负根,
由根与系数关系可知这两个根的积为 <0,
所以ac<0.所以方程(※)有一个正根和一个负根?
ac<0,从而ac<0?方程(※)有一个正根和一个负
根,因此ac<0是方程(※)有一个正根和一个负根的
充要条件.【类题·通】
充要条件的证明策略
(1)要证明一个条件p是否是q的充要条件,需要从充分性和必要性两个方向进行,即证明两个命题“若p,则q”为真且“若q,则p”为真.(2)在证明的过程中也可以转化为集合的思想来证明,证明p与q的解集是相同的,证明前必须分清楚充分性和必要性,即搞清楚由哪些条件推证到哪些结论.
提醒:证明时一定要注意,分清充分性与必要性的证明方向.【习练·破】
已知x,y都是非零实数,且x>y,判断xy>0是否是
的充要条件.【证明】由xy>0及x>y,得
所以xy>0?
即 <0,
又由x>y,得y-x<0,所以xy>0.
所以 ?xy>0,从而xy>0? ,
所以xy>0是 的充要条件.【加练·固】
求关于x的方程ax2+x+1=0至少有一个负实根的充要条件.【解析】①当a=0时,解得x=-1,满足条件;
②当a≠0时,显然方程没有零根,若方程有两异号实根,则a<0;
若方程有两个负的实根,
则必须满足 综上,若方程至少有一个负的实根,则a≤ .
反之,若a≤ ,则方程至少有一个负的实根.
因此,关于x的方程ax2+x+1=0至少有一个负实根的充
要条件是a≤ .类型三 用集合观点解充分条件、必要条件问题
【典例】1.已知p:点M(1-a,2a+6)在第四象限,
q:a<1,则p是q的 ( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件2.已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围. 世纪金榜导学号【思维·引】1.第四象限内的点横坐标大于0,纵坐标小于0.依据“小范围”推“大范围”,“大范围”推不出“小范围”判断;
2.先把p,q等价转化,利用充分条件、必要条件、充要条件与集合间的包含关系,建立关于m的不等式(组)进行求解.【解析】1.选A.因为点M(1-a,2a+6)在第四象限,
所以 解得a<-3.
因为(-∞,-3) (-∞,1),
所以p?q,q p,
所以p是q的充分不必要条件.2.p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的必要不充分条件,
所以q是p的充分不必要条件,
即[1-m,1+m] [-2,10],
故有 解得m≤3.
又m>0,所以实数m的取值范围为(0,3].【素养·探】
在与用集合观点解充分条件、必要条件问题中,经常
利用核心素养中的直观想象,通过研究充分条件和必
要条件与集合关系,培养借助集合解决问题的能力.
将本例2的“p是q的必要不充分条件”改为“p是q的充
分不必要条件”,其他条件不变,求实数m的取值范围.【解析】p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的充分不必要条件,
设p代表的集合为A,q代表的集合为B,
所以A B.
所以 解不等式组得m>9或m≥9,
所以m≥9,
即实数m的取值范围是[9,+∞).【类题·通】
从集合的角度判断充分条件、必要条件和充要条件其中p:A={x|p(x)成立},q:B={x|q(x)成立}.【习练·破】
设p:实数x满足a
所以(2,5] (a,4a)则 得 得
已知p:-1
所以(-1,3) [k-2,k+5],
所以
?-2≤k≤1.
所以实数k的取值范围是[-2,1].
