2.3.3 等比数列的前n项和 课件(25张PPT)
文档属性
| 名称 | 2.3.3 等比数列的前n项和 课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 15:59:25 | ||
图片预览








文档简介
(共25张PPT)
走运的一天:
2019年1月30日晚,我散步的时候遇到一个神秘的陌生人,他找我谈一个换钱的计划,该计划如下:
1.从下个月1日开始,陌生人每天给我十万元,
2.我第一天付对方一分钱,第二天付两分钱,第三天付四分钱,以此类推,我每天给对方的钱是前一天的两倍,直到月末最后一天。
我应该接受这个契约么?
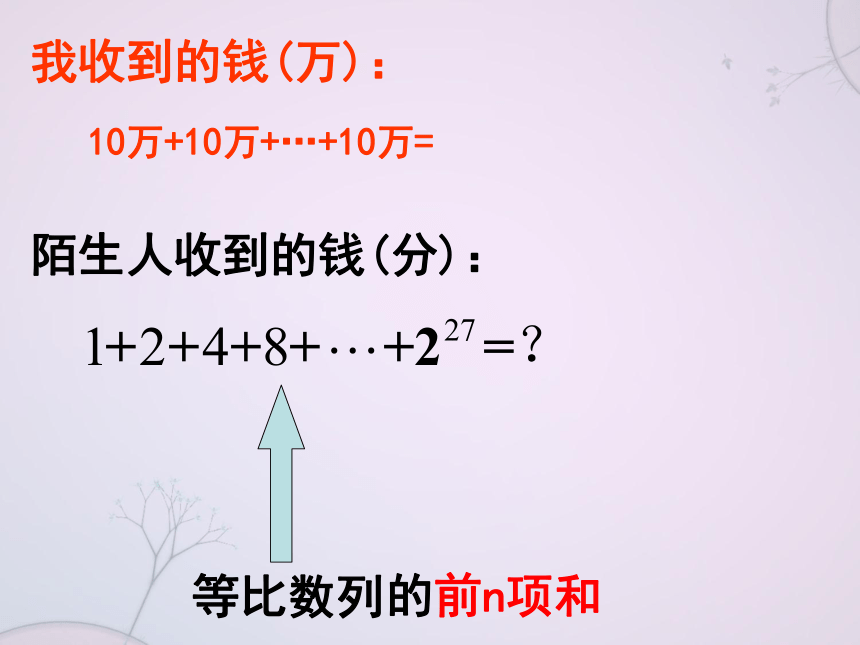
我收到的钱(万):
10万+10万+…+10万=
陌生人收到的钱(分):
等比数列
的前n项和
—公式、思想及应用
一、问题的提出
二、推而广之
如何求一般等比数列的前n项和Sn?
如何求等比数列的Sn:
①
②
①-② ,得
错位相减法
(q≠1)
等比数列前n项和公式:
思考:那q=1怎么办呢?
提示:q=1说明数列有什么特点?
(q≠1)
2.推导公式的方法:错位相减法。
注意:
等比数列前n项和公式:
当
时,
或
当q=1时,
n+1
判断是非
n
③
2
n
或0
公式运用
例1:求等比数列 的前8项和.
解:
例2.
解法1:
②
①
③
③代入②得
代入③得:n=5.
解法2
例3.某商场今年销售计算机5000台,如果平均每年的销售量比上一年的销售量增加10%,那么从今起,大约几年可使总销售量达到30000台(结果保留到个位)?
分析:第1年产量为 5000台
第2年产量为
5000×(1+10%)=5000×1.1台
第3年产量为
5000×(1+10%) ×(1+10%)
……
第n年产量为
则n年内的总产量为:
例3.某商场第一年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第一年起,约几年内可使总销售量达到30000台(保留到个位)?
答:约5年内可以使总销售量达到30000台.
三、再议求和公式
四、数学文化中的等比数列:
四、数学文化中的等比数列:
无穷递缩等比数列:
无穷递缩等比数列:
五、总结:
等差数列 等比数列
定义
通项公式
性质
Sn
五、总结:
注意记忆等比数列前n项和公式;
理解公式推导方法:错位相减法
2.应用前n项和公式时注意对公比分类讨论,
注意求和数列的项数;
3.面对实际应用问题时,通过观察发现问题
中的等比数列模型,选取合适的公式进行
通项或前n项和的求解
走运的一天:
2019年1月30日晚,我散步的时候遇到一个神秘的陌生人,他找我谈一个换钱的计划,该计划如下:
1.从下个月1日开始,陌生人每天给我十万元,
2.我第一天付对方一分钱,第二天付两分钱,第三天付四分钱,以此类推,我每天给对方的钱是前一天的两倍,直到月末最后一天。
我应该接受这个契约么?
我收到的钱(万):
10万+10万+…+10万=
陌生人收到的钱(分):
等比数列
的前n项和
—公式、思想及应用
一、问题的提出
二、推而广之
如何求一般等比数列的前n项和Sn?
如何求等比数列的Sn:
①
②
①-② ,得
错位相减法
(q≠1)
等比数列前n项和公式:
思考:那q=1怎么办呢?
提示:q=1说明数列有什么特点?
(q≠1)
2.推导公式的方法:错位相减法。
注意:
等比数列前n项和公式:
当
时,
或
当q=1时,
n+1
判断是非
n
③
2
n
或0
公式运用
例1:求等比数列 的前8项和.
解:
例2.
解法1:
②
①
③
③代入②得
代入③得:n=5.
解法2
例3.某商场今年销售计算机5000台,如果平均每年的销售量比上一年的销售量增加10%,那么从今起,大约几年可使总销售量达到30000台(结果保留到个位)?
分析:第1年产量为 5000台
第2年产量为
5000×(1+10%)=5000×1.1台
第3年产量为
5000×(1+10%) ×(1+10%)
……
第n年产量为
则n年内的总产量为:
例3.某商场第一年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第一年起,约几年内可使总销售量达到30000台(保留到个位)?
答:约5年内可以使总销售量达到30000台.
三、再议求和公式
四、数学文化中的等比数列:
四、数学文化中的等比数列:
无穷递缩等比数列:
无穷递缩等比数列:
五、总结:
等差数列 等比数列
定义
通项公式
性质
Sn
五、总结:
注意记忆等比数列前n项和公式;
理解公式推导方法:错位相减法
2.应用前n项和公式时注意对公比分类讨论,
注意求和数列的项数;
3.面对实际应用问题时,通过观察发现问题
中的等比数列模型,选取合适的公式进行
通项或前n项和的求解
