2.1 圆锥曲线 课件(21张PPT)
图片预览








文档简介
(共21张PPT)
*
我们一起观察
实验:在锥形瓶中注入一些有色液体,通过不断调整锥形瓶的位置,观察水面的图形.
问题:有哪些可能的图形呢?
我们一起观察
实验:在锥形瓶中注入一些有色液体,通过不断调整锥形瓶的位置,观察水面的图形.
问题:有哪些可能的图形呢?
现象:圆形,扁圆形(椭圆形)……
我们一起想象
实验:在锥形瓶中注入一些有色液体,通过不断调整锥形瓶的位置,观察水面的图形.
问题:除了圆,椭圆,还可能什么有图形呢?
那让我们一起再来观察吧!
(苏教版选修2-1第2章)
江苏省苏州中学 刘炜
圆锥曲线
什么是数学?
纯数学的对象是现实世界的空间形式和数量关系.
——恩格斯
现实世界
数学模型
抽象
我们一起对比
数学公理化的基础为:原始概念(基本概念)+命题(公理).
圆
在平面内把线段OP绕着端点O旋转1周,端点P运动所形成的图形叫做圆,其中点O叫做圆心,线段OP叫做半径.
(苏科版九年级上册P38)
椭圆
英雄安在?
填补空白!
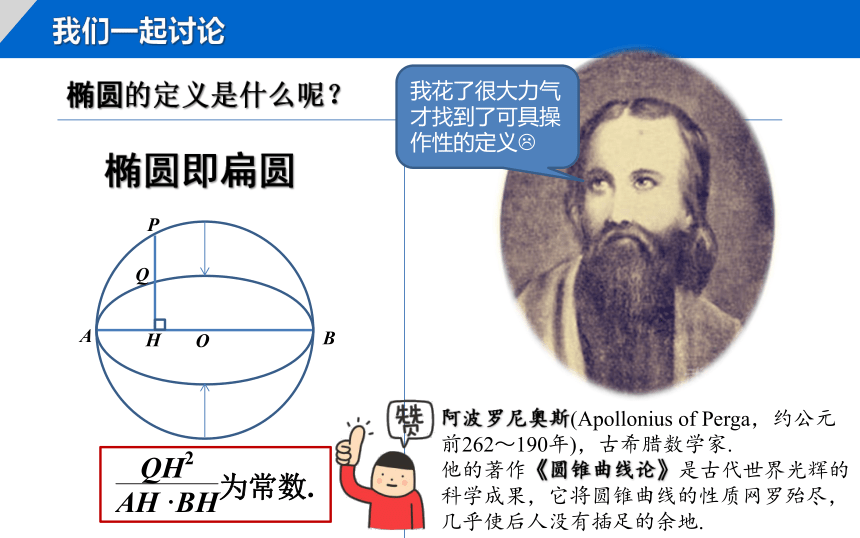
我们一起讨论
椭圆的定义是什么呢?
椭圆即扁圆
O
A
B
P
H
Q
阿波罗尼奥斯(Apollonius of Perga,约公元前262~190年),古希腊数学家.
他的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,
几乎使后人没有插足的余地.
我花了很大力气才找到了可具操作性的定义?
我们一起联想
Germinal Pierre Dandelin 1794-4-12-1847-2-15
数学家,工程学教授
牛顿遇到了苹果,
他发现了“万有引力”;
笛卡尔看到了蜘蛛网,
他发明了“坐标系”;
旦德林看了冰淇淋球,
会发生什么呢?
我们一起观察
研究的对象是:圆锥、大球、小球、截面.
它们之间什么关系呢?
(1)大球与圆锥相切,小球与圆锥相切;
(2)大球与截面相切,小球与截面相切.
我们研究重点是什么呢?
(1)圆锥与两球的切点集(C1, C2);
(2)截面与两球的切点(F1, F2);
与截线(椭圆)上点的数量关系!
听恩格斯的话:
研究什么数量关系?
我们一起探索
第一步:在椭圆上任取一点,标记为B;
第二步:将椭圆上的点A与截线上的点A重合,
滚动椭圆,将点对应在截线上,也记为B;
第三步:直线OB与两圆弧C1, C2分别交于S,T;
第四步:测量BS, BT, BF1, BF2 ;
第五步:研究上述四个量之间的关系!
BS = BF1 , BT = BF2 , BS+BT =ST .
我们一起验证
平面内到两个定点F1,F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆(ellipse),两个定点F1,F2叫做椭圆的焦点(focus),两焦点之间的距离叫做椭圆的焦距(focal distance).
因为BF1=BS,BF2=BT,所以BF1+BF2 =ST(定值).
椭圆的定义
实践验证:
步骤1:将细线固定在两个工字钉上,距离为10;
步骤2:将两个工字钉定在软木板上,距离为6;
步骤3:用笔尖把绳子拉紧,移动可画出椭圆.
我们一起应用
问题(课本练习,4):已知△ABC中,BC长为6,周长为16,那么顶点A在怎样的曲线上运动?
分析:AB+AC=10,符合椭圆定义.
猜测:顶点A在椭圆上运动.
实践反思:
椭圆上所有的点符合要求吗?
我们一起动手
操作:利用提供的材料包画出一个椭圆.
清单:软木板一张,工字钉两颗,细线一根(定长).
评选:在各组所画的椭圆中,你们认为哪个椭圆最美?
思考:什么样的椭圆是最美的呢?
步骤1:将两个工字钉定在软木板上,距离小于定长;
步骤2:用笔尖把绳子拉紧,移动可画出椭圆.
圆锥曲线的定义
平面内两个定点F1,F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆(ellipse),两个定点F1,F2叫做椭圆的焦点(focus),两焦点之间的距离叫做椭圆的焦距(focal distance).
平面内两个定点F1,F2的距离的差的绝对值等于常数(小于F1F2的正数) 的点的轨迹叫做双曲线(hyperbola),两个定点F1,F2叫做双曲线的焦点,两焦点之间的距离叫做双曲线的焦距.
平面内一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线(parabola),定点F叫做抛物线的焦点,定直线l叫做抛物线的准线(directrix).
类似地,可研究得:
圆锥曲线的发展
第一阶段:发现图形
约公元前4世纪,梅内克缪斯(希腊)利用垂直于母线的平面去截顶角是直角、钝角和锐角的圆锥,得到直角圆锥曲线(抛物线)、钝角圆锥曲线(双曲线)和锐角圆锥曲线(椭圆).
第二阶段:定义图形
约公元前3世纪,阿波罗尼奥斯(希腊)对同一个斜圆锥被不同位置的平面截得的曲线定义为圆锥曲线.并且用了7个命题、花了九牛二虎之力才偶然得到椭圆的定义,且完全脱离了圆锥.
第三阶段:应用图形
17世纪,笛卡尔(法国)对圆锥曲线方程的研究导致人们对椭圆曲线画法的探求,舒腾(法国)曾给出了椭圆的3种作图工具,其中一种即利用焦半径之和为常数的定义.
洛必达(法国)正式将椭圆定义提出,并推导椭圆的方程.
1822年,旦德林(比利时)才提出利用双球完成了截线定义与轨迹定义(第一定义)的统一.
我们的成长再现了历史的演变.
康德《纯粹理性批判》
(摘自波利亚《数学的发现》第14章引言)
人的认识从感觉开始,再从感觉上升到概念,最后形成思想。
问题探索1
问题1:一张相纸长为12cm,宽为8cm,在角落存在一个坏点,其距长边2.2cm,距短边2cm. 要在正中洗一个椭圆形照片,我们能不能避开这个坏点呢?
问题探索2
问题2:将圆压扁是不是符合椭圆的定义?
O
A
B
P
H
Q
研究设想:
1.假设椭圆,找到两个焦点;
2.验证椭圆上的到两焦点距离之和为定值.
我们需要椭圆的方程!
问题探索3
问题3:初中研究的抛物线、双曲线会不会恰好是某个平面截某个圆锥面得到的呢?
它们同名“同命” 吗?
让我们从实际生活出发,去做
数学的发现!
*
我们一起观察
实验:在锥形瓶中注入一些有色液体,通过不断调整锥形瓶的位置,观察水面的图形.
问题:有哪些可能的图形呢?
我们一起观察
实验:在锥形瓶中注入一些有色液体,通过不断调整锥形瓶的位置,观察水面的图形.
问题:有哪些可能的图形呢?
现象:圆形,扁圆形(椭圆形)……
我们一起想象
实验:在锥形瓶中注入一些有色液体,通过不断调整锥形瓶的位置,观察水面的图形.
问题:除了圆,椭圆,还可能什么有图形呢?
那让我们一起再来观察吧!
(苏教版选修2-1第2章)
江苏省苏州中学 刘炜
圆锥曲线
什么是数学?
纯数学的对象是现实世界的空间形式和数量关系.
——恩格斯
现实世界
数学模型
抽象
我们一起对比
数学公理化的基础为:原始概念(基本概念)+命题(公理).
圆
在平面内把线段OP绕着端点O旋转1周,端点P运动所形成的图形叫做圆,其中点O叫做圆心,线段OP叫做半径.
(苏科版九年级上册P38)
椭圆
英雄安在?
填补空白!
我们一起讨论
椭圆的定义是什么呢?
椭圆即扁圆
O
A
B
P
H
Q
阿波罗尼奥斯(Apollonius of Perga,约公元前262~190年),古希腊数学家.
他的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,
几乎使后人没有插足的余地.
我花了很大力气才找到了可具操作性的定义?
我们一起联想
Germinal Pierre Dandelin 1794-4-12-1847-2-15
数学家,工程学教授
牛顿遇到了苹果,
他发现了“万有引力”;
笛卡尔看到了蜘蛛网,
他发明了“坐标系”;
旦德林看了冰淇淋球,
会发生什么呢?
我们一起观察
研究的对象是:圆锥、大球、小球、截面.
它们之间什么关系呢?
(1)大球与圆锥相切,小球与圆锥相切;
(2)大球与截面相切,小球与截面相切.
我们研究重点是什么呢?
(1)圆锥与两球的切点集(C1, C2);
(2)截面与两球的切点(F1, F2);
与截线(椭圆)上点的数量关系!
听恩格斯的话:
研究什么数量关系?
我们一起探索
第一步:在椭圆上任取一点,标记为B;
第二步:将椭圆上的点A与截线上的点A重合,
滚动椭圆,将点对应在截线上,也记为B;
第三步:直线OB与两圆弧C1, C2分别交于S,T;
第四步:测量BS, BT, BF1, BF2 ;
第五步:研究上述四个量之间的关系!
BS = BF1 , BT = BF2 , BS+BT =ST .
我们一起验证
平面内到两个定点F1,F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆(ellipse),两个定点F1,F2叫做椭圆的焦点(focus),两焦点之间的距离叫做椭圆的焦距(focal distance).
因为BF1=BS,BF2=BT,所以BF1+BF2 =ST(定值).
椭圆的定义
实践验证:
步骤1:将细线固定在两个工字钉上,距离为10;
步骤2:将两个工字钉定在软木板上,距离为6;
步骤3:用笔尖把绳子拉紧,移动可画出椭圆.
我们一起应用
问题(课本练习,4):已知△ABC中,BC长为6,周长为16,那么顶点A在怎样的曲线上运动?
分析:AB+AC=10,符合椭圆定义.
猜测:顶点A在椭圆上运动.
实践反思:
椭圆上所有的点符合要求吗?
我们一起动手
操作:利用提供的材料包画出一个椭圆.
清单:软木板一张,工字钉两颗,细线一根(定长).
评选:在各组所画的椭圆中,你们认为哪个椭圆最美?
思考:什么样的椭圆是最美的呢?
步骤1:将两个工字钉定在软木板上,距离小于定长;
步骤2:用笔尖把绳子拉紧,移动可画出椭圆.
圆锥曲线的定义
平面内两个定点F1,F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆(ellipse),两个定点F1,F2叫做椭圆的焦点(focus),两焦点之间的距离叫做椭圆的焦距(focal distance).
平面内两个定点F1,F2的距离的差的绝对值等于常数(小于F1F2的正数) 的点的轨迹叫做双曲线(hyperbola),两个定点F1,F2叫做双曲线的焦点,两焦点之间的距离叫做双曲线的焦距.
平面内一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线(parabola),定点F叫做抛物线的焦点,定直线l叫做抛物线的准线(directrix).
类似地,可研究得:
圆锥曲线的发展
第一阶段:发现图形
约公元前4世纪,梅内克缪斯(希腊)利用垂直于母线的平面去截顶角是直角、钝角和锐角的圆锥,得到直角圆锥曲线(抛物线)、钝角圆锥曲线(双曲线)和锐角圆锥曲线(椭圆).
第二阶段:定义图形
约公元前3世纪,阿波罗尼奥斯(希腊)对同一个斜圆锥被不同位置的平面截得的曲线定义为圆锥曲线.并且用了7个命题、花了九牛二虎之力才偶然得到椭圆的定义,且完全脱离了圆锥.
第三阶段:应用图形
17世纪,笛卡尔(法国)对圆锥曲线方程的研究导致人们对椭圆曲线画法的探求,舒腾(法国)曾给出了椭圆的3种作图工具,其中一种即利用焦半径之和为常数的定义.
洛必达(法国)正式将椭圆定义提出,并推导椭圆的方程.
1822年,旦德林(比利时)才提出利用双球完成了截线定义与轨迹定义(第一定义)的统一.
我们的成长再现了历史的演变.
康德《纯粹理性批判》
(摘自波利亚《数学的发现》第14章引言)
人的认识从感觉开始,再从感觉上升到概念,最后形成思想。
问题探索1
问题1:一张相纸长为12cm,宽为8cm,在角落存在一个坏点,其距长边2.2cm,距短边2cm. 要在正中洗一个椭圆形照片,我们能不能避开这个坏点呢?
问题探索2
问题2:将圆压扁是不是符合椭圆的定义?
O
A
B
P
H
Q
研究设想:
1.假设椭圆,找到两个焦点;
2.验证椭圆上的到两焦点距离之和为定值.
我们需要椭圆的方程!
问题探索3
问题3:初中研究的抛物线、双曲线会不会恰好是某个平面截某个圆锥面得到的呢?
它们同名“同命” 吗?
让我们从实际生活出发,去做
数学的发现!
