2.2.2 椭圆的几何性质 课件(17张PPT)
文档属性
| 名称 | 2.2.2 椭圆的几何性质 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 515.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
解析几何彻底改变了数学的研究方法
--M·克莱因
材料:
我国发射的第一颗人造地球卫星的运行轨道是以地球的中心(简称“地心”)为一个焦点的椭圆.
已知它的近地点(离地面最近的点)距地面439km,远地点(离地面最远的点)距地面2384km,地球半径约为6371km.
问题情境
问题1 哪里是近地点,哪里是远地点呢?
苏教版普通高中课程标准实验教科书(选修2-1)
2017年江苏省高中数学优秀课观摩与评比
椭 圆 的 几 何 性 质
问题2 椭圆有哪些几何性质呢?
问题3 怎么样来研究呢?
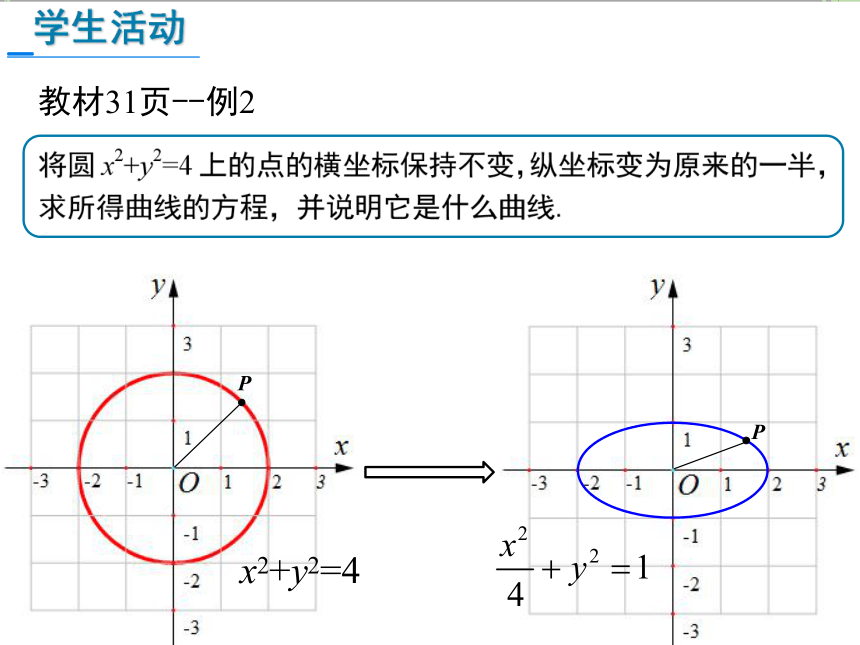
学生活动
x2+y2=4
教材31页--例2
P
P
学生活动
1.范围
方程中变量x , y的取值范围
椭圆的范围
以焦点在x轴上的椭圆为例
学生活动
F2
F1
y
O
x
-a
b
a
-b
形
数
坐标轴是椭圆的对称轴
原点是椭圆的对称中心
椭圆的对称中心叫做椭圆的中心
思考:椭圆的对称轴一定是坐标轴吗?
-a
F2
F1
b
y
O
x
a
-b
关于y轴对称
P1(-x,y)
P3(-x,-y)
P(x,y)
P2(x,-y)
学生活动
2.对称性
椭圆的对称性
关于x轴对称
关于原点对称
方程形式上的对称性
形
数
-a
F2
F1
b
y
O
x
a
-b
A2
B2
A1
B1
P
问题4 线段PO的长度何时最大?
何时最小?
学生活动
这四个点是对称轴与椭圆
的交点,称为椭圆的顶点.
学生活动
-a
F2
F1
b
y
O
x
a
-b
P
Q
a
c
把线段A1A2,线段B1B2分别叫椭圆的长轴和短轴,
它们的长分别等于2a和2b;
a和b分别叫做椭圆的长半轴的长和短半轴的长.
x=0或y=0时方程的解
椭圆与对称轴的交点
椭圆与坐标轴的交点
3.顶点
A2
B2
A1
B1
形
数
思考:离心率的范围是多少?
-a
F2
F1
b
y
O
x
a
-b
A2
B2
A1
B1
4.离心率
椭圆的圆扁程度
学生活动
形
数
数学运用
例题 我国发射的第一颗人造地球卫星的运行轨道是以地球的中心(简称“地心”) F2为一个焦点的椭圆.已知它的近地点A (离地面最近的点)距地面439km,远地点B(离地面最远的点)距地面2384km,AB是椭圆的长轴,地球半径约为6371km,求卫星运行的轨道方程.
.
数学运用
y
x
例题 我国发射的第一颗人造地球卫星的运行轨道是以地球的中心(简称“地心”) F2为一个焦点的椭圆.已知它的近地点A (离地面最近的点)距地面439km,远地点B(离地面最远的点)距地面2384km,AB是椭圆的长轴,地球半径约为6371km,求卫星运行的轨道方程.
椭圆的几何性质
标准方程
活动回顾
椭圆
代数方法
建系
方程的代数特征
图形观察
类比
数形结合
形
数
标准方程
图形
范围
对称性
顶点坐标
半轴长
离心率
关于x轴,y轴,原点对称
(±a,0),(0, ±b)
-a≤x≤a,-b≤y≤b
-a
F2
F1
b
y
O
x
a
-b
A1
A2
B1
B2
长半轴长为a,短半轴长为b
F2
F1
O
y
x
B2
B1
A1
A2
你能写出焦点在y轴的椭圆的几何性质吗?
活动回顾
1.椭圆图形本身的性质与坐标系的选择无关;
两个关注
活动回顾
2.离心率的刻画.
课外延展
谢 谢
THANK YOU
解析几何彻底改变了数学的研究方法
--M·克莱因
材料:
我国发射的第一颗人造地球卫星的运行轨道是以地球的中心(简称“地心”)为一个焦点的椭圆.
已知它的近地点(离地面最近的点)距地面439km,远地点(离地面最远的点)距地面2384km,地球半径约为6371km.
问题情境
问题1 哪里是近地点,哪里是远地点呢?
苏教版普通高中课程标准实验教科书(选修2-1)
2017年江苏省高中数学优秀课观摩与评比
椭 圆 的 几 何 性 质
问题2 椭圆有哪些几何性质呢?
问题3 怎么样来研究呢?
学生活动
x2+y2=4
教材31页--例2
P
P
学生活动
1.范围
方程中变量x , y的取值范围
椭圆的范围
以焦点在x轴上的椭圆为例
学生活动
F2
F1
y
O
x
-a
b
a
-b
形
数
坐标轴是椭圆的对称轴
原点是椭圆的对称中心
椭圆的对称中心叫做椭圆的中心
思考:椭圆的对称轴一定是坐标轴吗?
-a
F2
F1
b
y
O
x
a
-b
关于y轴对称
P1(-x,y)
P3(-x,-y)
P(x,y)
P2(x,-y)
学生活动
2.对称性
椭圆的对称性
关于x轴对称
关于原点对称
方程形式上的对称性
形
数
-a
F2
F1
b
y
O
x
a
-b
A2
B2
A1
B1
P
问题4 线段PO的长度何时最大?
何时最小?
学生活动
这四个点是对称轴与椭圆
的交点,称为椭圆的顶点.
学生活动
-a
F2
F1
b
y
O
x
a
-b
P
Q
a
c
把线段A1A2,线段B1B2分别叫椭圆的长轴和短轴,
它们的长分别等于2a和2b;
a和b分别叫做椭圆的长半轴的长和短半轴的长.
x=0或y=0时方程的解
椭圆与对称轴的交点
椭圆与坐标轴的交点
3.顶点
A2
B2
A1
B1
形
数
思考:离心率的范围是多少?
-a
F2
F1
b
y
O
x
a
-b
A2
B2
A1
B1
4.离心率
椭圆的圆扁程度
学生活动
形
数
数学运用
例题 我国发射的第一颗人造地球卫星的运行轨道是以地球的中心(简称“地心”) F2为一个焦点的椭圆.已知它的近地点A (离地面最近的点)距地面439km,远地点B(离地面最远的点)距地面2384km,AB是椭圆的长轴,地球半径约为6371km,求卫星运行的轨道方程.
.
数学运用
y
x
例题 我国发射的第一颗人造地球卫星的运行轨道是以地球的中心(简称“地心”) F2为一个焦点的椭圆.已知它的近地点A (离地面最近的点)距地面439km,远地点B(离地面最远的点)距地面2384km,AB是椭圆的长轴,地球半径约为6371km,求卫星运行的轨道方程.
椭圆的几何性质
标准方程
活动回顾
椭圆
代数方法
建系
方程的代数特征
图形观察
类比
数形结合
形
数
标准方程
图形
范围
对称性
顶点坐标
半轴长
离心率
关于x轴,y轴,原点对称
(±a,0),(0, ±b)
-a≤x≤a,-b≤y≤b
-a
F2
F1
b
y
O
x
a
-b
A1
A2
B1
B2
长半轴长为a,短半轴长为b
F2
F1
O
y
x
B2
B1
A1
A2
你能写出焦点在y轴的椭圆的几何性质吗?
活动回顾
1.椭圆图形本身的性质与坐标系的选择无关;
两个关注
活动回顾
2.离心率的刻画.
课外延展
谢 谢
THANK YOU
