六年级上册数学课件-第1课时 数与形(1) 人教版(共25张PPT)
文档属性
| 名称 | 六年级上册数学课件-第1课时 数与形(1) 人教版(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-11 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
数与形(1)
探究新知
基础练习
拓展练习
课堂小结
数学阅读
人教版数学六年级上册 第八单元
情景导入
请同学们用最快的速度计算下面的算式的结果。
1+3+5+7+9+11+13+…+99=?
超级神算:只要从1开始的连续奇数相加,我都能脱口而出,你相信吗?
1+3=( )
4
1+3 +5=( )
9
1+3+5+7=( )
16
1+3+5+7+9+11+13+15+17+19=( )
100
你发现了什么?
探究新知
从1开始的连续奇数相加的和,正好是这些奇数的个数的平方。
计算出结果。
2个奇数相加
3个奇数相加
4个奇数相加
10个奇数相加
基础练习
挑战第一关
从1开始,5个连续奇数相加等于多少?
从1开始,11个连续奇数相加等于多少?
从1开始,连续奇数相加,加到23时,结果是多少?
从1开始,连续奇数相加,加到79时,结果是多少?
连续奇数个数
奇数本身
1
2
3
4
5
1
3
5
7
9
加到23时,是多少个连续奇数相加?
25
121
加到79时,是多少个连续奇数相加?
连续奇数个数
奇数本身
×2-1
=
(奇数本身
连续奇数个数
+1)÷2
=
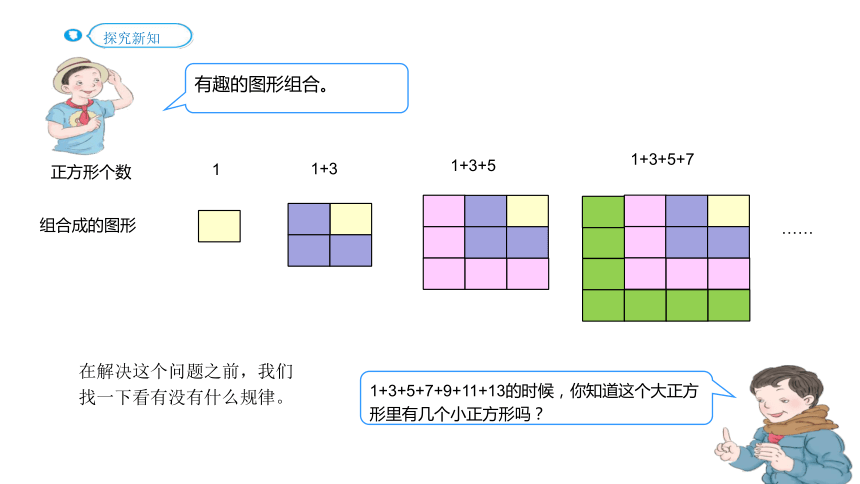
有趣的图形组合。
探究新知
1
正方形个数
组合成的图形
1+3
1+3+5
1+3+5+7
……
1+3+5+7+9+11+13的时候,你知道这个大正方形里有几个小正方形吗?
在解决这个问题之前,我们找一下看有没有什么规律。
有趣的图形组合
探究新知
1
正方形个数
组合成的图形
1+3
1+3+5
1+3+5+7
……
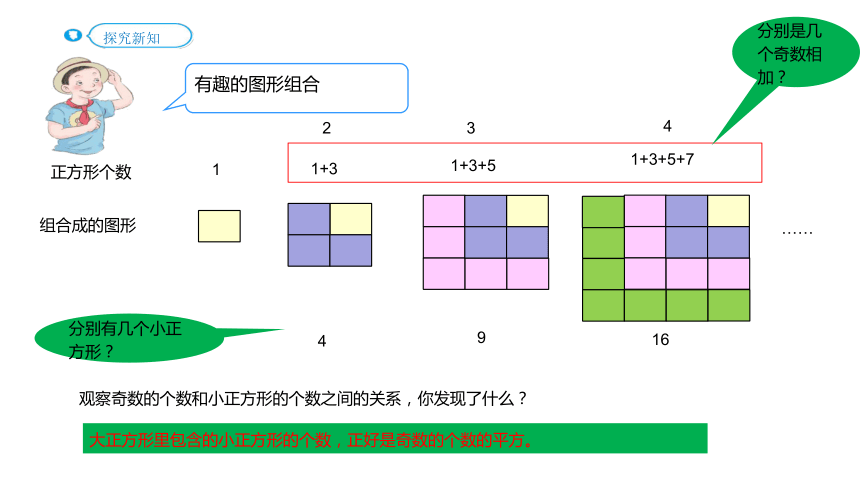
分别是几个奇数相加?
2
分别有几个小正方形?
4
3
4
9
16
观察奇数的个数和小正方形的个数之间的关系,你发现了什么?
大正方形里包含的小正方形的个数,正好是奇数的个数的平方。
有趣的图形组合
探究新知
1
正方形个数
组合成的图形
1+3
1+3+5
1+3+5+7
……
1+3+5+7+9+11+13的时候,你知道这个大正方形里有几个小正方形吗?
这个问题你现在会回答了吗?
这是7个连续奇数相加,所以组成的大正方形里含有的小正方形的个数应该是7的平方,即49个。
挑战第二关
基础练习
从1开始,5个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
从1开始,10个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
从1开始,15个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
25
100
225
探究新知
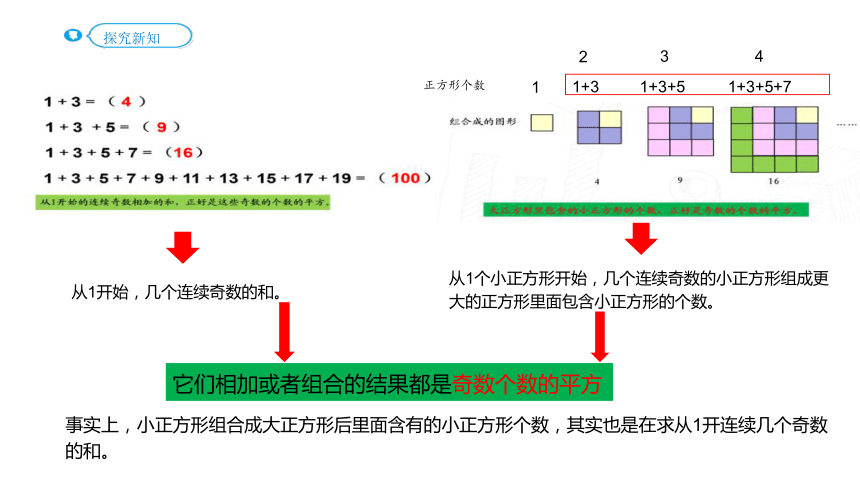
从1开始,几个连续奇数的和。
从1个小正方形开始,几个连续奇数的小正方形组成更大的正方形里面包含小正方形的个数。
它们相加或者组合的结果都是奇数个数的平方
事实上,小正方形组合成大正方形后里面含有的小正方形个数,其实也是在求从1开连续几个奇数的和。
正方形个数
1
1+3
1+3+5
1+3+5+7
2
3
4
探究新知
所以,我们以上的探究结果可以用一句话来描述,那就是:
从1开始,连续奇数的和,就是奇数个数的平方。
1+3+5+7=( )
1+3+5+7+9+11+13 =( )
1. 你能利用规律直接写一写吗?
4
7
如果遇到困难,可以画图来帮助。
1+3+5+7+9+11+13+15+17
=9
2
2
2
基础练习
2. 5个连续奇数个小正方形组成的大正方形,如果小正方形的边长为2cm,那么大正方形的面积是多少平方米?它的周长呢?
基础练习
大正方形里有几个小正方形?它的边长由几个小正方形拼成?
1+3+5+7+5+3+1 =( )
1.你能快速说出结果吗?
25
可以看成两部分:1+3+5+7=42
5+3+1= 32
42+ 32 =25
拓展练习
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
85
2. 下面每个图中最外圈有多少个小正方形?
拓展练习
(1)两个连续图形大正方形边长与前面一个小正方形边长之间有什么关系?
1
3
5
7
这些图形的边长是从1开始的连续奇数。
(2)第二个图形的边长是多少?第三个图形的边长是多少?……
第二个图形的边长是3,第三个图形的边长是5
1. 下面每个图中最外圈有多少个小正方形?
拓展练习
(3)你发现了什么规律?
第几图,这个图的边长就是第几个奇数。
如:第二个图的边长是第二个奇数3,第三个图的边长是第3个奇数5,第四个图的边长是第四第4个奇数7
1. (1)下面每个图中最外圈有多少个小正方形?
拓展练习
(4)大正方形最外圈有多少个小正方形,我们可以用什么方法计算?
1
3
5
7
大正方形面积-小正方形面积
(5)你有什么发现?
边长:
1. (2)按这样画下去,画到第5个图形,这个图形最外圈有多少个小正方形?
拓展练习
8
16
24
?
(1)第5个图形的边长是几?
32
从1开始,第5个连续奇数,即:1,3,5,7,9,这个图形的边长是9。
(2)第5个图形最外圈小正方形个数怎么计算?
1. (3)按这样画下去,画到第7个图形,这个图形最外圈有多少个小正方形?
拓展练习
8
16
24
?
(1)第7个图形的边长是谁?
48
从1开始,第5个连续奇数,即:1,3,5,7,9,11,13。这个图形的边长是13。
(2)第7个图形最外圈小正方形个数怎么计算?
1. (4)按这样画下去,画到第35个图形,这个图形最外圈有多少个小正方形?
拓展练习
(1)第35个图形的边长是多少?
奇数个数×2-1=奇数本身,(奇数本身+1)÷2=奇数个数。
1,3,5,7,……
(2)还记得奇数个数与奇数本身的关系吗?即第几个奇数是多少,或者说知道奇数本身,想要知道它是第几个奇数。
2. (4)按这样画下去,画到第35个图形,这个图形最外圈有多少个小正方形?
拓展练习
(3)那么,第35个图形的边长是多少?
奇数个数×2-1=奇数本身
35×2-1=69
(4)第35个图形最外圈有多少个小正方形?
拓展练习
2. 按照规律接着画一画填一填。
如果不画,你知道第8个图有几个圆吗?第18个?第35个呢?
3
1
6
10
1+2
1+2+3
1+2+3+4
1
2
3
4
图的个数
图里的圆数
发现1:画第几个图,就是在前一个图的基础上加几,如第4个图,就是在前一个图上再加4;
发现2:画到第n个图,这个图里圆的个数就是1+2+3+…+n。比如画到第3个图时,这个图里的个数就是1+2+3,画到第5个图时,这个图里圆的个数就是1+2+3+4+5。
拓展练习
你会算吗?
+7+8+9+10+11
1+2+3+4+5+
6
12
12
12
12
12
1、12是怎么得来的?
2、一共有这样的几个12?
(1+11)
×
首尾相加
12的个数
+6
6是怎么算出来的?
(1+11)
×
×
=
(1+11)
66
拓展练习
你会算吗?
+7+8+9+10+11+…+n(n是奇数时)
1+2+3+4+5+
6
(1+n)×
1+2+3+4+5+6+7+8+…+n(n是偶数时)
(1+n)
×
发现:连续自然数相加的和=
(1+n)×
n
2
拓展练习
2. 按照规律接着画一画填一填。
如果不画,你知道第8个图有几个圆吗?第18个?第35个呢?
3
1
6
10
1+2
1+2+3
1+2+3+4
1
2
3
4
图的个数
图里的圆数
第8个图形里的圆个数就是1+2+3+…+8
第18个图形里的圆个数就是1+2+3+…+18
第35个图形里的圆个数就是1+2+3+…+35
36
171
630
数学阅读
1
1+3
1+3+5
1+3+5+7
这些数量的方块都能排成正方形,所以我们把它叫做正方形数。
1+2
1
1+2+3
1+2+3+4
这些数量的图形都可以排成三角形,所以我们把它叫做三角形数。
正方形数和三角形数
数与形(1)
探究新知
基础练习
拓展练习
课堂小结
数学阅读
人教版数学六年级上册 第八单元
情景导入
请同学们用最快的速度计算下面的算式的结果。
1+3+5+7+9+11+13+…+99=?
超级神算:只要从1开始的连续奇数相加,我都能脱口而出,你相信吗?
1+3=( )
4
1+3 +5=( )
9
1+3+5+7=( )
16
1+3+5+7+9+11+13+15+17+19=( )
100
你发现了什么?
探究新知
从1开始的连续奇数相加的和,正好是这些奇数的个数的平方。
计算出结果。
2个奇数相加
3个奇数相加
4个奇数相加
10个奇数相加
基础练习
挑战第一关
从1开始,5个连续奇数相加等于多少?
从1开始,11个连续奇数相加等于多少?
从1开始,连续奇数相加,加到23时,结果是多少?
从1开始,连续奇数相加,加到79时,结果是多少?
连续奇数个数
奇数本身
1
2
3
4
5
1
3
5
7
9
加到23时,是多少个连续奇数相加?
25
121
加到79时,是多少个连续奇数相加?
连续奇数个数
奇数本身
×2-1
=
(奇数本身
连续奇数个数
+1)÷2
=
有趣的图形组合。
探究新知
1
正方形个数
组合成的图形
1+3
1+3+5
1+3+5+7
……
1+3+5+7+9+11+13的时候,你知道这个大正方形里有几个小正方形吗?
在解决这个问题之前,我们找一下看有没有什么规律。
有趣的图形组合
探究新知
1
正方形个数
组合成的图形
1+3
1+3+5
1+3+5+7
……
分别是几个奇数相加?
2
分别有几个小正方形?
4
3
4
9
16
观察奇数的个数和小正方形的个数之间的关系,你发现了什么?
大正方形里包含的小正方形的个数,正好是奇数的个数的平方。
有趣的图形组合
探究新知
1
正方形个数
组合成的图形
1+3
1+3+5
1+3+5+7
……
1+3+5+7+9+11+13的时候,你知道这个大正方形里有几个小正方形吗?
这个问题你现在会回答了吗?
这是7个连续奇数相加,所以组成的大正方形里含有的小正方形的个数应该是7的平方,即49个。
挑战第二关
基础练习
从1开始,5个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
从1开始,10个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
从1开始,15个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
25
100
225
探究新知
从1开始,几个连续奇数的和。
从1个小正方形开始,几个连续奇数的小正方形组成更大的正方形里面包含小正方形的个数。
它们相加或者组合的结果都是奇数个数的平方
事实上,小正方形组合成大正方形后里面含有的小正方形个数,其实也是在求从1开连续几个奇数的和。
正方形个数
1
1+3
1+3+5
1+3+5+7
2
3
4
探究新知
所以,我们以上的探究结果可以用一句话来描述,那就是:
从1开始,连续奇数的和,就是奇数个数的平方。
1+3+5+7=( )
1+3+5+7+9+11+13 =( )
1. 你能利用规律直接写一写吗?
4
7
如果遇到困难,可以画图来帮助。
1+3+5+7+9+11+13+15+17
=9
2
2
2
基础练习
2. 5个连续奇数个小正方形组成的大正方形,如果小正方形的边长为2cm,那么大正方形的面积是多少平方米?它的周长呢?
基础练习
大正方形里有几个小正方形?它的边长由几个小正方形拼成?
1+3+5+7+5+3+1 =( )
1.你能快速说出结果吗?
25
可以看成两部分:1+3+5+7=42
5+3+1= 32
42+ 32 =25
拓展练习
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
85
2. 下面每个图中最外圈有多少个小正方形?
拓展练习
(1)两个连续图形大正方形边长与前面一个小正方形边长之间有什么关系?
1
3
5
7
这些图形的边长是从1开始的连续奇数。
(2)第二个图形的边长是多少?第三个图形的边长是多少?……
第二个图形的边长是3,第三个图形的边长是5
1. 下面每个图中最外圈有多少个小正方形?
拓展练习
(3)你发现了什么规律?
第几图,这个图的边长就是第几个奇数。
如:第二个图的边长是第二个奇数3,第三个图的边长是第3个奇数5,第四个图的边长是第四第4个奇数7
1. (1)下面每个图中最外圈有多少个小正方形?
拓展练习
(4)大正方形最外圈有多少个小正方形,我们可以用什么方法计算?
1
3
5
7
大正方形面积-小正方形面积
(5)你有什么发现?
边长:
1. (2)按这样画下去,画到第5个图形,这个图形最外圈有多少个小正方形?
拓展练习
8
16
24
?
(1)第5个图形的边长是几?
32
从1开始,第5个连续奇数,即:1,3,5,7,9,这个图形的边长是9。
(2)第5个图形最外圈小正方形个数怎么计算?
1. (3)按这样画下去,画到第7个图形,这个图形最外圈有多少个小正方形?
拓展练习
8
16
24
?
(1)第7个图形的边长是谁?
48
从1开始,第5个连续奇数,即:1,3,5,7,9,11,13。这个图形的边长是13。
(2)第7个图形最外圈小正方形个数怎么计算?
1. (4)按这样画下去,画到第35个图形,这个图形最外圈有多少个小正方形?
拓展练习
(1)第35个图形的边长是多少?
奇数个数×2-1=奇数本身,(奇数本身+1)÷2=奇数个数。
1,3,5,7,……
(2)还记得奇数个数与奇数本身的关系吗?即第几个奇数是多少,或者说知道奇数本身,想要知道它是第几个奇数。
2. (4)按这样画下去,画到第35个图形,这个图形最外圈有多少个小正方形?
拓展练习
(3)那么,第35个图形的边长是多少?
奇数个数×2-1=奇数本身
35×2-1=69
(4)第35个图形最外圈有多少个小正方形?
拓展练习
2. 按照规律接着画一画填一填。
如果不画,你知道第8个图有几个圆吗?第18个?第35个呢?
3
1
6
10
1+2
1+2+3
1+2+3+4
1
2
3
4
图的个数
图里的圆数
发现1:画第几个图,就是在前一个图的基础上加几,如第4个图,就是在前一个图上再加4;
发现2:画到第n个图,这个图里圆的个数就是1+2+3+…+n。比如画到第3个图时,这个图里的个数就是1+2+3,画到第5个图时,这个图里圆的个数就是1+2+3+4+5。
拓展练习
你会算吗?
+7+8+9+10+11
1+2+3+4+5+
6
12
12
12
12
12
1、12是怎么得来的?
2、一共有这样的几个12?
(1+11)
×
首尾相加
12的个数
+6
6是怎么算出来的?
(1+11)
×
×
=
(1+11)
66
拓展练习
你会算吗?
+7+8+9+10+11+…+n(n是奇数时)
1+2+3+4+5+
6
(1+n)×
1+2+3+4+5+6+7+8+…+n(n是偶数时)
(1+n)
×
发现:连续自然数相加的和=
(1+n)×
n
2
拓展练习
2. 按照规律接着画一画填一填。
如果不画,你知道第8个图有几个圆吗?第18个?第35个呢?
3
1
6
10
1+2
1+2+3
1+2+3+4
1
2
3
4
图的个数
图里的圆数
第8个图形里的圆个数就是1+2+3+…+8
第18个图形里的圆个数就是1+2+3+…+18
第35个图形里的圆个数就是1+2+3+…+35
36
171
630
数学阅读
1
1+3
1+3+5
1+3+5+7
这些数量的方块都能排成正方形,所以我们把它叫做正方形数。
1+2
1
1+2+3
1+2+3+4
这些数量的图形都可以排成三角形,所以我们把它叫做三角形数。
正方形数和三角形数
