高一数学苏教版必修5第一章:解三角形综合复习学案(含答案)
文档属性
| 名称 | 高一数学苏教版必修5第一章:解三角形综合复习学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 14:51:28 | ||
图片预览


文档简介
解三角形综合
在碰到几何图形中不止一个三角形,或者需要我们解几多个三角形的时;
解题关键:把同一个边或角放到不同的三角形中利用正余弦定理求出,然后建立等量关系;
常用定理:正弦定理,余弦定理,三角形的外角定理,两角和与差公式等.
例1.在△ABC中,D是边AC上的点,且AB=AD,2AB=BD,BC=2BD,则的值为________.
例2.设△ABC的内角A,B,C所对的边长分别为,且
(1)求角A的大小;
(2)若角,BC边上的中线AM的长为,求△ABC的面积.
例3.在△ABC中,角A,B,C的对边分别为,已知.
(1)求角B的大小;
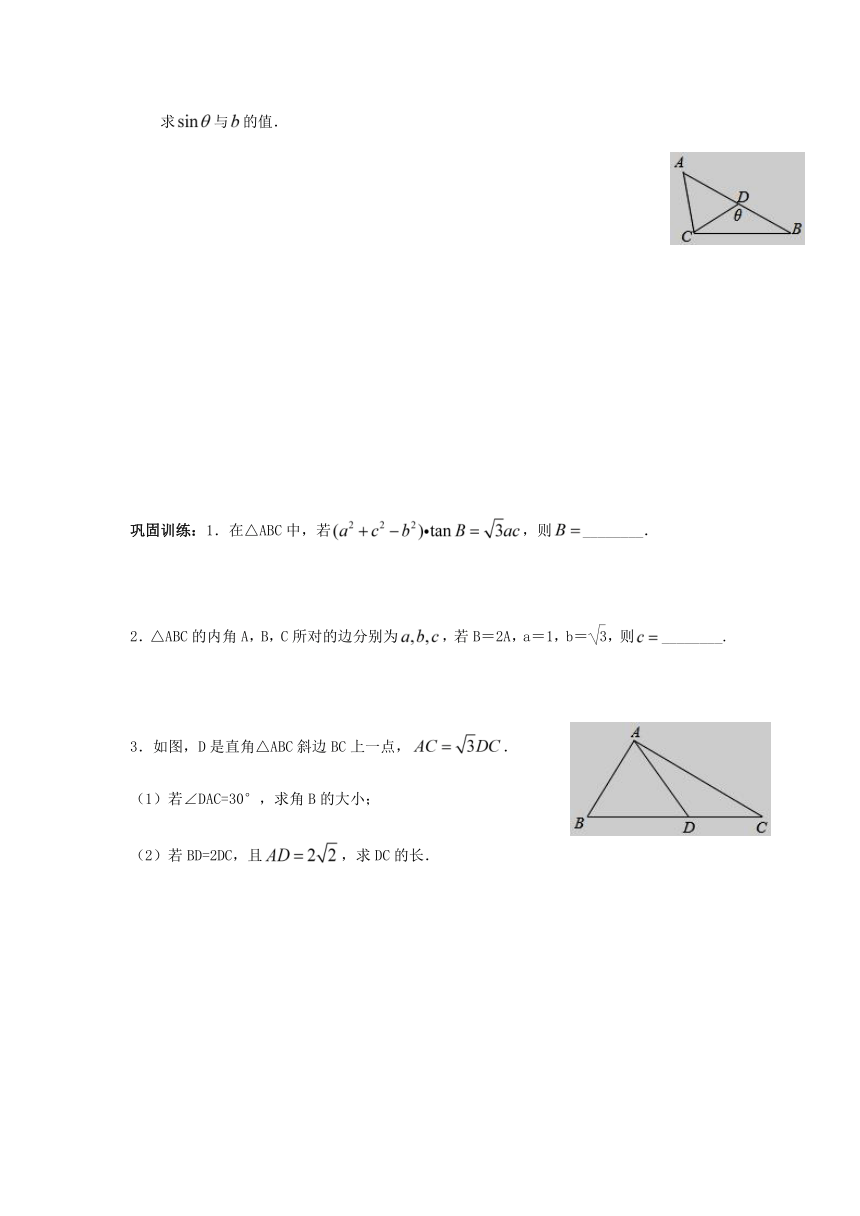
(2)点D为边AB上的一点,记。若,,,求与的值.
巩固训练:1.在△ABC中,若,则________.
2.△ABC的内角A,B,C所对的边分别为,若B=2A,a=1,b=,则________.
3.如图,D是直角△ABC斜边BC上一点,.
(1)若∠DAC=30°,求角B的大小;
(2)若BD=2DC,且,求DC的长.
4.如图,已知△ABC中,D为BC上一点,,,.
(1)求AD的长;
(2)若△ABD的面积为14,求AB的长.
例4.如图,在中,B=,角A的平分线AD交BC于点D,设,.
(1)求和;
(2)若,求AC的长.
例5.已知函数.
(1)求函数的单调递减区间;
(2)在中,角的对边分别为,若,的面积为,求的最小值.
巩固训练:1.如图,在△中,是边上的点,且,,则的值为 .
2.在中,角A,B,C所对的边分别是,若.
(1)求角A的大小;
(2)若,求的面积.
3.如图,在△ABC中,,,.
(1)求的值;
(2)设的中点为,求中线的长.
参 考 答 案
例1. 例2.(1);(2) 例3.(1);(2)
巩固练习:1. 2.2 3.(1);(2)2 4.(1)7;(2)
例4.(1) 例5.(1);(2)
巩固训练:1. 2.(1);(2) 3.(1);(2)
