六年级下册数学课件 4.1 比例的意义与性质 苏教版 (共62张PPT)
文档属性
| 名称 | 六年级下册数学课件 4.1 比例的意义与性质 苏教版 (共62张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 749.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 13:50:21 | ||
图片预览











文档简介
(共62张PPT)
正比例的意义
…
信息: 一张连云港连岛海滨浴场的门票是50元,4张、5张、6张……各要多少元?
150
100
50
总价(元)
…
6
5
4
3
2
1
数量(张)
200
250
300
1、统计表中有哪两种量?它们有什么关系?
2、从左到右观察这些数据你有什么发现?
3、你能分别写出相对应的总价和数量的比吗?比值是多少?看看比值你发现了什么?它表示什么?
4 、如果我们用字母y、x表示这两种量,用k表示它们的比值应该怎么写?
两种相关联的量,一种量变化,另一种量也随着变化,
这两种量中相对应的两个数的比的比值(也就是商)一定,
它们之间的关系叫做正比例关系。
这两种量就叫做成正比例的量,
如果
精讲点拨
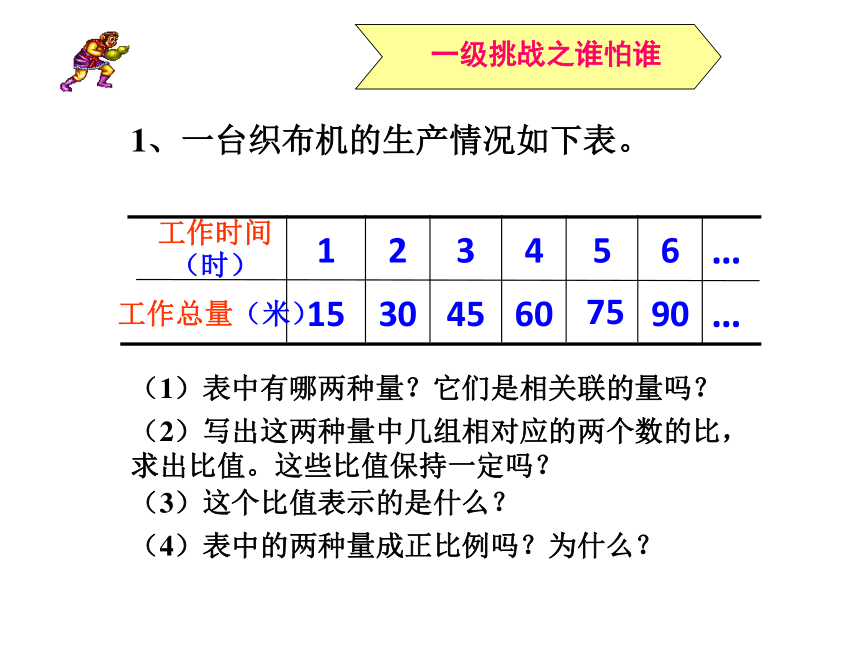
1、一台织布机的生产情况如下表。
…
90
60
45
30
15
工作总量(米)
…
6
5
4
3
2
1
工作时间(时)
75
(1)表中有哪两种量?它们是相关联的量吗?
(2)写出这两种量中几组相对应的两个数的比,求出比值。这些比值保持一定吗?
(3)这个比值表示的是什么?
(4)表中的两种量成正比例吗?为什么?
一级挑战之谁怕谁
2、判断两种量是否成正比例。
(1)飞机飞行的速度一定,飞行的路程与飞行的时间。
(2)订阅《小学生数学报》的份数和总钱数。
(3)圆的周长和它的直径。
(4)小刚骑车的速度一定,已行的路程与剩下的路程。
二级挑战之火眼金睛
(√)
(√)
(×)
(√)
???
下列题里有哪两种相关联的量?这两种量成不成正比例?为什么?
一种苹果,买5千克要10元。照这样计算,买15千克要30元。
三级挑战之我怕谁
连岛卖票处声称:如果买10张门票以下,每张50元;如果买10张门票以上(包括10张),每张40元. 请问总价同门票的数量是不是成正比例, 如果成正比例, 那是在什么情况?
终极挑战之生活中的数学
比例的意义
苏教版六年级数学下册
1、什么是比的意义?
2、比的基本性质是什么?
3、比的各部分名称是什么?
4、比值怎么求?
6.4厘米
4厘米
9.6厘米
6厘米
1、分别写出每张照片长和宽的比。
2、然后化简比并求出比值。
6.4 : 4 =
9.6 : 6 =
6.4 : 4 =
9.6 : 6 =
8 : 5
8 : 5
1.6
1.6
化简比:
求比值:
表示两个比相等的式子叫做比例。
6.4
4
9.6
6
=
=
比例的意义:
6.4︰4
9.6︰6
分别写出照片放大后与放大前长的比和宽的比,这两个比也能组成比例吗?
6.4厘米
4厘米
9.6厘米
6厘米
9.6 : 6.4 = 3 :2
6 : 4= 3 : 2
9.6 : 6.4 =
3
2
6 : 4 =
3
2
这两个比能组成比例。
或
9.6 :6.4=6 :4
想一想:
怎样判断两个比是否能
组成比例?
如果两个比化简后的比相同
或它们的比值相等,这两个
比就能组成比例。
比较“比”和“比例”的不同
比表示两个数相除,有两项。
比例是一个等式,表示两个比相等,有四项。
长:5m 宽:10/3m
长:2.4m宽:1.6m
分别写出两面国旗长和宽的比
判断这两面国旗的比是否能组成比例
哪几组的两个比可以组成比例?把组成的比例写下来。
练一练
(1)10 12和25 30
:
:
(2)2 8和9 27
:
:
1
8
(4) 和
1
4
1
8
1
16
:
:
(3)0.9 3和
:
1
15
1
5
:
判断下面哪个比能与 组
成比例。
1
5
: 4
(1)5 : 4
(2)20 : 1
(3)1 : 20
1
4
(4)5 :
一辆汽车上午4小时行驶了320千米,下午3小时行驶了240千米。
320 :4
(2)下午行驶的路程和时间的比是
(3)这两个比能组成比例吗?为什么?
240 :3
(1)上午行驶的路程和时间的比是
320 4=240 3
:
:
两次行驶路程的比和两次行驶时间的比也能组成比例吗?
320 240=4 3
:
:
全课小结
同学们回顾一下,你在本课有什么收获?
苏教版六年级数学下册
什么叫做比例?
什么样的两个比才能组成比例?
下面每组中两个比能组成比例吗?请利用比例的意义说一说。
3 : 5 18 : 30
0.4 :0.2 1.8 :0.9
6cm
4cm
3cm
2cm
你能根据图中的数据写出不同的比例吗?
把左边的三角形按比例缩小后得到右边的三角形。
6 3 = 4 2 4 2=6 3
6 4=3 2
4 6=2 3
:
:
:
:
:
:
:
:
内项
外项
观察这些比例,你有什么发现?
你能说出其它三个比例的外项和内项各是多少吗?
在其它的比例里,是不是也有两个外项的积等于两个内项的积这样的规律呢?
5 4=15 12
:
:
0.2 1= 0.6 3
:
:
:
:
1
3
1
4
2
3
1
2
=
如果用字母表示比例的四个项,即a :b=c :d,那么这个规律可以表示成
a×d=b×c
在比例里,两个外项的积等于两个内项的积。
在比例里,两个内项的积等于两个外项的积,这叫做比例的基本性质。
6 :3=4 : 2
6
3
=
4
2
如果把比例写成分数形式,请你说一说外项和内项。
6×2=4×3
应用比例的基本性质,判断下面
的两个比能否组成比例。如能组成
比例,把组成的比例写出来。
3.6:1.8和0.5:0.25
( )×( )=( )
( )×( )=( )
1.8 0.5 0.9
3.6 0.25 0.9
3.6 :1.8=0.5 :025
0.5 :0.25=3.6 :1.8
根据比例的基本性质,在括号里填上合适的数。
( ) :6=4 :( )
5 : ( ) =( ) :8
练一练
3 8
4 10
一列火车从甲城开往乙城,行驶速度和所需时间如下表。
练一练
速度/(千米/时) 80 120 160
时间/时 6 4 3
(1)从表中选择两组数据,写出一个乘积相等的式子。
(2)根据上面的等式,写出一个比例。
哪一组中的四个数可以组成比例?
把组成的比例写出来。
(1)6、4、18和12
(2)4、5、6和8
练一练
6 4=18 12 4 6=12 18
4 12=6 18 12 4=18 6
:
:
:
:
:
:
:
:
应用比例的基本性质,判断下面哪几组的两个比可以组成比例。把组成的比例写出来。
(1)14 21和 6 9(2)
:
:
3
10
3
4
和
15
2
:
1
:
:
:
(3)9 12和12 15(4)1.4 2和7 10
:
:
学校航模小组有男生18人,女生15人;
美术组有男生24人,女生20人。
(1)航模组男、女生人数的比和美术组男、女生人数的比能组成比例吗?
(2)如果可以组成比例,指出比例的内项和外项。
18 15=24 20
:
:
把图A按比例放大得到图B,按比例缩小得到图C。根据图中的数据组成比例。
12厘米
9厘米
15厘米
4厘米
3厘米
5厘米
10厘米
8厘米
6厘米
A B C
8 6=12 9 8 6 = 4 3
8 10= 12 15 12 15 = 4 5
:
:
:
:
:
:
:
:
:
:
8 2=24( )
( )
15
=
4
5
根据比例的基本性质,在括号里填上合适的数。
1.5 3=( )3.4
:
:
48 ( )=3.6 9
:
:
6
12
1.7
120
思考题
在一个比例中,两个外项正好互为倒数,已知一个内项是 ,另一个内项是( )
16
3
3
16
已知5x=3y,则x:y=( ):( )。
如果x=6,则y =( )。
3 5
10
3 :5 = 6 :10 4 .5 :9
比例
比
表示两个比相等的式子
两个数相除
从意义上
从结构名称上
有4个项:两个外项,
两个内项
有2个项:
前项和后项
等号连接两个比(=)
比和比例:
比例的基本性质是什么呢?你觉得学了它有什么用处?
比例的基本性质
通过预习你有什么疑惑吗?
1、你能根据例4图中的数据写出几个不同的比例吗?
2、比例的各部分名称是什么?请举例说明。
一、交流预习
两个三角形底的比和高的比相等。
两个三角形高的比和底的比相等。
每个三角形底和高的比相等。
每个三角形高和底的比相等。
3 : 6 = 2 : 4
内项
外项
组成比例的 个数,叫做比例的 。
两端的两项叫做比例的 ,中间的两项叫做比例的 。
(四)
(项 )
(外项)
(内项)
你能说出其它比例的内项和外项是多少吗?
如果把比例写成分数形式或含有分数的等式,你还能指出它的内项和外项吗?
=
⑴
=
⑵
=
⑶
:
:
4
1、仔细观察、比较前面的几个比例,它们内项和外项的数有什么特点?它们有什么相同点和规律吗?
2、比例的基本性质是什么?
3、比和比例有什么区别?
二、互助探究
如果用字母表示比例的四个项,即ɑ:b=c:d,那么ɑ和d可以同时是比例的外项,也可以同时是比例的内项。b和c也可以同时是比例的内项或外项。
ɑ×d = b×c
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
可以表示为( )
如果把比例写成分数形式,把等号两端的分子、分母分别交叉相乘结果怎样?
2×9=3×6
=
⑴
=
⑵
=
⑶
:
:
4
把比例ɑ:b=c:d写成分数形式,怎样写?
写出把等号两端的分子、分母分别交叉相乘的积
ɑ×d = b×c
比和比例有什么区别
比 比例
意义
构成及各部分名称
基本
性质
两个数相除又叫做两个数的比。
表示两个比相等的式子叫做比例。
由两个数组成,分别叫比的前项和后项。
由四个数组成,两端的两项叫做比例的外项,中间的两项叫做比例的内项。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
1、你能运用比例的基本性质来解决问题吗?
2、独立完成后交流,要细心哦!
三、巩固提高
应用比例的基本性质,判断下面的两个比能否组成比例。如果能组成比例,把组成的比例写出来。
⑴3.6 : 1.8 和 0.5 : 0.25
( )×( )=( )
( )×( )=( )
挑战一:
和
⑵
:
:
18
24
( )×( )=( )
( )×( )=( )
挑战二:
( )
3
10
=
15
()︰3=4︰( )
4.5
4
2
5
1
︰
1
=
1
︰
( )
2
5
挑战三:
5 ︰()=( )︰6
根据比例的基本性质,填空。
能与2、5、8组成比例的数, 可能是( )。
挑战四:
2、你对你的师、友有何评价建议?
1、通过这节课的学习,你有哪些收获?还有什么疑问?
四、归纳总结
正比例的意义
…
信息: 一张连云港连岛海滨浴场的门票是50元,4张、5张、6张……各要多少元?
150
100
50
总价(元)
…
6
5
4
3
2
1
数量(张)
200
250
300
1、统计表中有哪两种量?它们有什么关系?
2、从左到右观察这些数据你有什么发现?
3、你能分别写出相对应的总价和数量的比吗?比值是多少?看看比值你发现了什么?它表示什么?
4 、如果我们用字母y、x表示这两种量,用k表示它们的比值应该怎么写?
两种相关联的量,一种量变化,另一种量也随着变化,
这两种量中相对应的两个数的比的比值(也就是商)一定,
它们之间的关系叫做正比例关系。
这两种量就叫做成正比例的量,
如果
精讲点拨
1、一台织布机的生产情况如下表。
…
90
60
45
30
15
工作总量(米)
…
6
5
4
3
2
1
工作时间(时)
75
(1)表中有哪两种量?它们是相关联的量吗?
(2)写出这两种量中几组相对应的两个数的比,求出比值。这些比值保持一定吗?
(3)这个比值表示的是什么?
(4)表中的两种量成正比例吗?为什么?
一级挑战之谁怕谁
2、判断两种量是否成正比例。
(1)飞机飞行的速度一定,飞行的路程与飞行的时间。
(2)订阅《小学生数学报》的份数和总钱数。
(3)圆的周长和它的直径。
(4)小刚骑车的速度一定,已行的路程与剩下的路程。
二级挑战之火眼金睛
(√)
(√)
(×)
(√)
???
下列题里有哪两种相关联的量?这两种量成不成正比例?为什么?
一种苹果,买5千克要10元。照这样计算,买15千克要30元。
三级挑战之我怕谁
连岛卖票处声称:如果买10张门票以下,每张50元;如果买10张门票以上(包括10张),每张40元. 请问总价同门票的数量是不是成正比例, 如果成正比例, 那是在什么情况?
终极挑战之生活中的数学
比例的意义
苏教版六年级数学下册
1、什么是比的意义?
2、比的基本性质是什么?
3、比的各部分名称是什么?
4、比值怎么求?
6.4厘米
4厘米
9.6厘米
6厘米
1、分别写出每张照片长和宽的比。
2、然后化简比并求出比值。
6.4 : 4 =
9.6 : 6 =
6.4 : 4 =
9.6 : 6 =
8 : 5
8 : 5
1.6
1.6
化简比:
求比值:
表示两个比相等的式子叫做比例。
6.4
4
9.6
6
=
=
比例的意义:
6.4︰4
9.6︰6
分别写出照片放大后与放大前长的比和宽的比,这两个比也能组成比例吗?
6.4厘米
4厘米
9.6厘米
6厘米
9.6 : 6.4 = 3 :2
6 : 4= 3 : 2
9.6 : 6.4 =
3
2
6 : 4 =
3
2
这两个比能组成比例。
或
9.6 :6.4=6 :4
想一想:
怎样判断两个比是否能
组成比例?
如果两个比化简后的比相同
或它们的比值相等,这两个
比就能组成比例。
比较“比”和“比例”的不同
比表示两个数相除,有两项。
比例是一个等式,表示两个比相等,有四项。
长:5m 宽:10/3m
长:2.4m宽:1.6m
分别写出两面国旗长和宽的比
判断这两面国旗的比是否能组成比例
哪几组的两个比可以组成比例?把组成的比例写下来。
练一练
(1)10 12和25 30
:
:
(2)2 8和9 27
:
:
1
8
(4) 和
1
4
1
8
1
16
:
:
(3)0.9 3和
:
1
15
1
5
:
判断下面哪个比能与 组
成比例。
1
5
: 4
(1)5 : 4
(2)20 : 1
(3)1 : 20
1
4
(4)5 :
一辆汽车上午4小时行驶了320千米,下午3小时行驶了240千米。
320 :4
(2)下午行驶的路程和时间的比是
(3)这两个比能组成比例吗?为什么?
240 :3
(1)上午行驶的路程和时间的比是
320 4=240 3
:
:
两次行驶路程的比和两次行驶时间的比也能组成比例吗?
320 240=4 3
:
:
全课小结
同学们回顾一下,你在本课有什么收获?
苏教版六年级数学下册
什么叫做比例?
什么样的两个比才能组成比例?
下面每组中两个比能组成比例吗?请利用比例的意义说一说。
3 : 5 18 : 30
0.4 :0.2 1.8 :0.9
6cm
4cm
3cm
2cm
你能根据图中的数据写出不同的比例吗?
把左边的三角形按比例缩小后得到右边的三角形。
6 3 = 4 2 4 2=6 3
6 4=3 2
4 6=2 3
:
:
:
:
:
:
:
:
内项
外项
观察这些比例,你有什么发现?
你能说出其它三个比例的外项和内项各是多少吗?
在其它的比例里,是不是也有两个外项的积等于两个内项的积这样的规律呢?
5 4=15 12
:
:
0.2 1= 0.6 3
:
:
:
:
1
3
1
4
2
3
1
2
=
如果用字母表示比例的四个项,即a :b=c :d,那么这个规律可以表示成
a×d=b×c
在比例里,两个外项的积等于两个内项的积。
在比例里,两个内项的积等于两个外项的积,这叫做比例的基本性质。
6 :3=4 : 2
6
3
=
4
2
如果把比例写成分数形式,请你说一说外项和内项。
6×2=4×3
应用比例的基本性质,判断下面
的两个比能否组成比例。如能组成
比例,把组成的比例写出来。
3.6:1.8和0.5:0.25
( )×( )=( )
( )×( )=( )
1.8 0.5 0.9
3.6 0.25 0.9
3.6 :1.8=0.5 :025
0.5 :0.25=3.6 :1.8
根据比例的基本性质,在括号里填上合适的数。
( ) :6=4 :( )
5 : ( ) =( ) :8
练一练
3 8
4 10
一列火车从甲城开往乙城,行驶速度和所需时间如下表。
练一练
速度/(千米/时) 80 120 160
时间/时 6 4 3
(1)从表中选择两组数据,写出一个乘积相等的式子。
(2)根据上面的等式,写出一个比例。
哪一组中的四个数可以组成比例?
把组成的比例写出来。
(1)6、4、18和12
(2)4、5、6和8
练一练
6 4=18 12 4 6=12 18
4 12=6 18 12 4=18 6
:
:
:
:
:
:
:
:
应用比例的基本性质,判断下面哪几组的两个比可以组成比例。把组成的比例写出来。
(1)14 21和 6 9(2)
:
:
3
10
3
4
和
15
2
:
1
:
:
:
(3)9 12和12 15(4)1.4 2和7 10
:
:
学校航模小组有男生18人,女生15人;
美术组有男生24人,女生20人。
(1)航模组男、女生人数的比和美术组男、女生人数的比能组成比例吗?
(2)如果可以组成比例,指出比例的内项和外项。
18 15=24 20
:
:
把图A按比例放大得到图B,按比例缩小得到图C。根据图中的数据组成比例。
12厘米
9厘米
15厘米
4厘米
3厘米
5厘米
10厘米
8厘米
6厘米
A B C
8 6=12 9 8 6 = 4 3
8 10= 12 15 12 15 = 4 5
:
:
:
:
:
:
:
:
:
:
8 2=24( )
( )
15
=
4
5
根据比例的基本性质,在括号里填上合适的数。
1.5 3=( )3.4
:
:
48 ( )=3.6 9
:
:
6
12
1.7
120
思考题
在一个比例中,两个外项正好互为倒数,已知一个内项是 ,另一个内项是( )
16
3
3
16
已知5x=3y,则x:y=( ):( )。
如果x=6,则y =( )。
3 5
10
3 :5 = 6 :10 4 .5 :9
比例
比
表示两个比相等的式子
两个数相除
从意义上
从结构名称上
有4个项:两个外项,
两个内项
有2个项:
前项和后项
等号连接两个比(=)
比和比例:
比例的基本性质是什么呢?你觉得学了它有什么用处?
比例的基本性质
通过预习你有什么疑惑吗?
1、你能根据例4图中的数据写出几个不同的比例吗?
2、比例的各部分名称是什么?请举例说明。
一、交流预习
两个三角形底的比和高的比相等。
两个三角形高的比和底的比相等。
每个三角形底和高的比相等。
每个三角形高和底的比相等。
3 : 6 = 2 : 4
内项
外项
组成比例的 个数,叫做比例的 。
两端的两项叫做比例的 ,中间的两项叫做比例的 。
(四)
(项 )
(外项)
(内项)
你能说出其它比例的内项和外项是多少吗?
如果把比例写成分数形式或含有分数的等式,你还能指出它的内项和外项吗?
=
⑴
=
⑵
=
⑶
:
:
4
1、仔细观察、比较前面的几个比例,它们内项和外项的数有什么特点?它们有什么相同点和规律吗?
2、比例的基本性质是什么?
3、比和比例有什么区别?
二、互助探究
如果用字母表示比例的四个项,即ɑ:b=c:d,那么ɑ和d可以同时是比例的外项,也可以同时是比例的内项。b和c也可以同时是比例的内项或外项。
ɑ×d = b×c
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
可以表示为( )
如果把比例写成分数形式,把等号两端的分子、分母分别交叉相乘结果怎样?
2×9=3×6
=
⑴
=
⑵
=
⑶
:
:
4
把比例ɑ:b=c:d写成分数形式,怎样写?
写出把等号两端的分子、分母分别交叉相乘的积
ɑ×d = b×c
比和比例有什么区别
比 比例
意义
构成及各部分名称
基本
性质
两个数相除又叫做两个数的比。
表示两个比相等的式子叫做比例。
由两个数组成,分别叫比的前项和后项。
由四个数组成,两端的两项叫做比例的外项,中间的两项叫做比例的内项。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
1、你能运用比例的基本性质来解决问题吗?
2、独立完成后交流,要细心哦!
三、巩固提高
应用比例的基本性质,判断下面的两个比能否组成比例。如果能组成比例,把组成的比例写出来。
⑴3.6 : 1.8 和 0.5 : 0.25
( )×( )=( )
( )×( )=( )
挑战一:
和
⑵
:
:
18
24
( )×( )=( )
( )×( )=( )
挑战二:
( )
3
10
=
15
()︰3=4︰( )
4.5
4
2
5
1
︰
1
=
1
︰
( )
2
5
挑战三:
5 ︰()=( )︰6
根据比例的基本性质,填空。
能与2、5、8组成比例的数, 可能是( )。
挑战四:
2、你对你的师、友有何评价建议?
1、通过这节课的学习,你有哪些收获?还有什么疑问?
四、归纳总结
