人教B版数学必修一 3.1.2 指数函数课件(共20张ppt)
文档属性
| 名称 | 人教B版数学必修一 3.1.2 指数函数课件(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 00:00:00 | ||
图片预览





文档简介
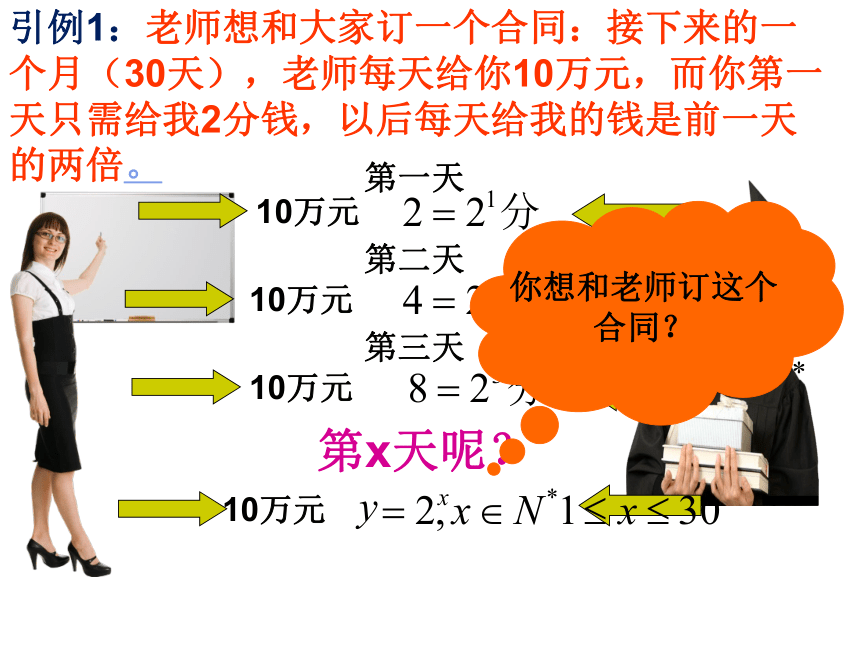
课件20张PPT。指数函数引例1:老师想和大家订一个合同:接下来的一个月(30天),老师每天给你10万元,而你第一天只需给我2分钱,以后每天给我的钱是前一天的两倍。第x天呢?第一天第二天10万元10万元第三天10万元10万元你想和老师订这个
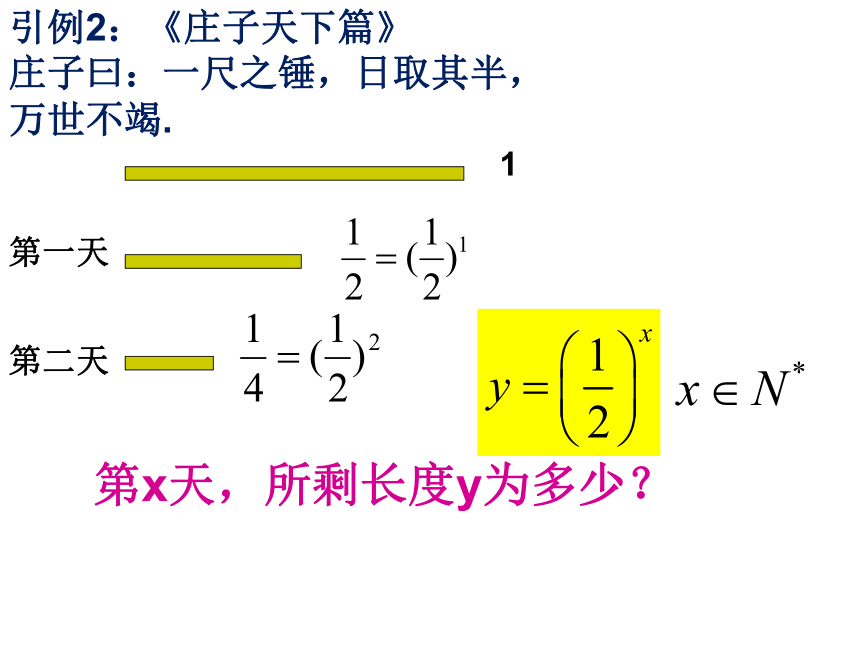
合同?1引例2:《庄子天下篇》
庄子曰:一尺之锤,日取其半,
万世不竭.第x天,所剩长度y为多少?第一天第二天引入概念我们从上面两个例子中抽象得到两个表达式:问题一:它们是函数吗?问题二:它们有什么共同特征呢? 一般地,形如y = ax(a?0,且a ?1)
的函数叫做指数函数,其中x是自
变量 .指数函数的定义 概念剖析当a=1时,a x 恒等于1,没有研究的必要.探究1:为何规定a?0,且a?1 ?探究2:指数式a x中X∈R都有意义吗 ? 回顾上一节的内容,我们发现指数式 ab 中b可以是 有理数也可以是无理数,所以指数函数的定义域是R. 当a<0时,a x有些会没有意义,如 当a=0时,a x有些会没有意义,如 概念剖析小试牛刀:下列函数是不是指数函数?为什么?(1) y=x2
y=2x
(3) y=2-x
(4) y=2 · 3x
(5) y=(-2)x
(6) y=3x+1
的系数是1 ;
指数必须是单个x ;
底数a?0,且a?1.指数函数的解析式 ,探究3:指数函数
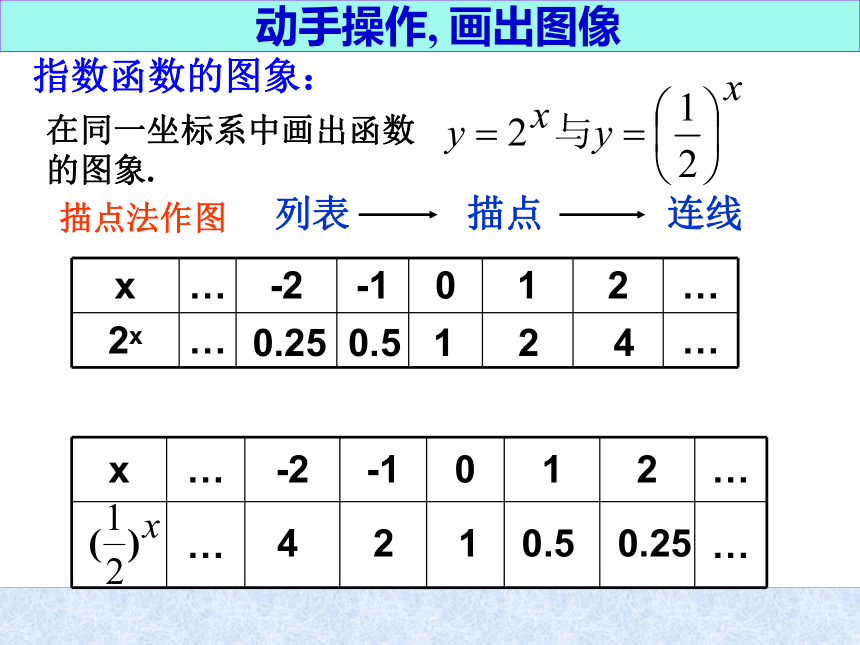
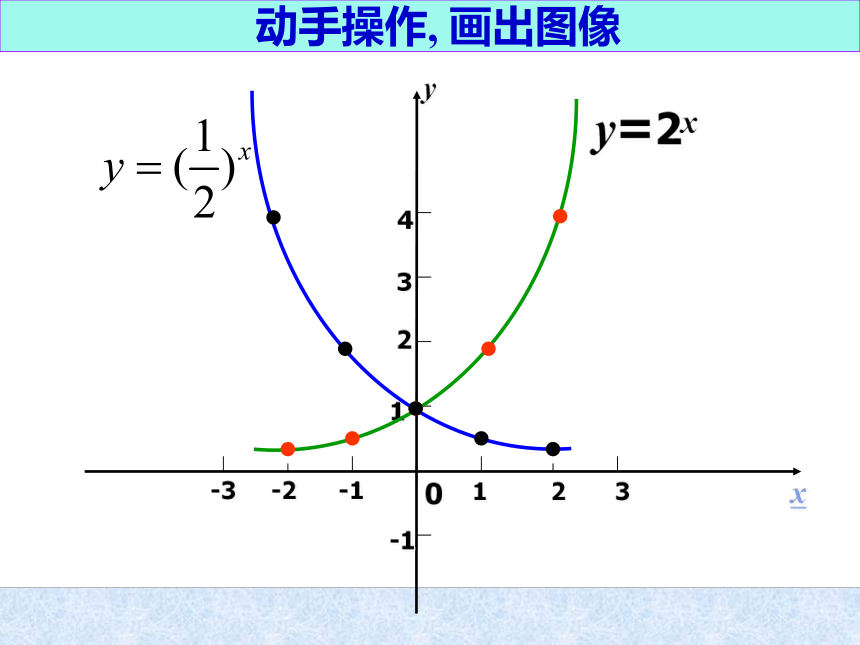
解析式有什么特点?动手操作, 画出图像指数函数的图象: 在同一坐标系中画出函数 的图象. 描点法作图0.25 0.5 1 2 4 4 2 1 0.5 0.25动手操作, 画出图像-1 1 2 3-3 -2 -143210yxy=2x 图 象 性 质a>10(a>1)yx(0,1)y=10y=ax
(00,y>1; x<0,y>1; x<0, 00,0 (1)1.72.5 , 1.73 ;
(2)0.8-0.1 ,0.8 -0.2
求满足下列条件的实数x的范围:
x≤3X<-31、比较大小1.70.3 , 0.93.12、当 时,试比
较 的大小中间值法:找一个 “中间值”如“1”来过渡,
数的特征是底不同指不同。1、求下面函数的定义域
(1) (2 ) (3)
2、下面函数式指数函数吗
(1) (2)3、已知y=f(x)是指数函数,且f(2)=4,求函数y=f(x)的解析式. 4、 比较大小:
(1)3.10.5 , 3.12.3
(2)
(3) 2.3-2.5 , 0.2 -0.1<><5、指数函数 中的
6、若指数函数 是减函数,求实数 的取值范围. -27、
感悟收获,巩固拓展我掌握了哪些数学方法? 我学到了哪些数学知识? 谈谈你这节课的收获!分类讨论,划归思想,数形结合华罗庚:数缺形时少直观;
形缺数时难入微。
合同?1引例2:《庄子天下篇》
庄子曰:一尺之锤,日取其半,
万世不竭.第x天,所剩长度y为多少?第一天第二天引入概念我们从上面两个例子中抽象得到两个表达式:问题一:它们是函数吗?问题二:它们有什么共同特征呢? 一般地,形如y = ax(a?0,且a ?1)
的函数叫做指数函数,其中x是自
变量 .指数函数的定义 概念剖析当a=1时,a x 恒等于1,没有研究的必要.探究1:为何规定a?0,且a?1 ?探究2:指数式a x中X∈R都有意义吗 ? 回顾上一节的内容,我们发现指数式 ab 中b可以是 有理数也可以是无理数,所以指数函数的定义域是R. 当a<0时,a x有些会没有意义,如 当a=0时,a x有些会没有意义,如 概念剖析小试牛刀:下列函数是不是指数函数?为什么?(1) y=x2
y=2x
(3) y=2-x
(4) y=2 · 3x
(5) y=(-2)x
(6) y=3x+1
的系数是1 ;
指数必须是单个x ;
底数a?0,且a?1.指数函数的解析式 ,探究3:指数函数
解析式有什么特点?动手操作, 画出图像指数函数的图象: 在同一坐标系中画出函数 的图象. 描点法作图0.25 0.5 1 2 4 4 2 1 0.5 0.25动手操作, 画出图像-1 1 2 3-3 -2 -143210yxy=2x 图 象 性 质a>10
(0
(2)0.8-0.1 ,0.8 -0.2
求满足下列条件的实数x的范围:
x≤3X<-31、比较大小1.70.3 , 0.93.12、当 时,试比
较 的大小中间值法:找一个 “中间值”如“1”来过渡,
数的特征是底不同指不同。1、求下面函数的定义域
(1) (2 ) (3)
2、下面函数式指数函数吗
(1) (2)3、已知y=f(x)是指数函数,且f(2)=4,求函数y=f(x)的解析式. 4、 比较大小:
(1)3.10.5 , 3.12.3
(2)
(3) 2.3-2.5 , 0.2 -0.1<><5、指数函数 中的
6、若指数函数 是减函数,求实数 的取值范围. -27、
感悟收获,巩固拓展我掌握了哪些数学方法? 我学到了哪些数学知识? 谈谈你这节课的收获!分类讨论,划归思想,数形结合华罗庚:数缺形时少直观;
形缺数时难入微。
