北师大数学九年级下册课件:3.3 垂径定理(共16张PPT)
文档属性
| 名称 | 北师大数学九年级下册课件:3.3 垂径定理(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 840.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
第三章 圆
3.3 垂径定理
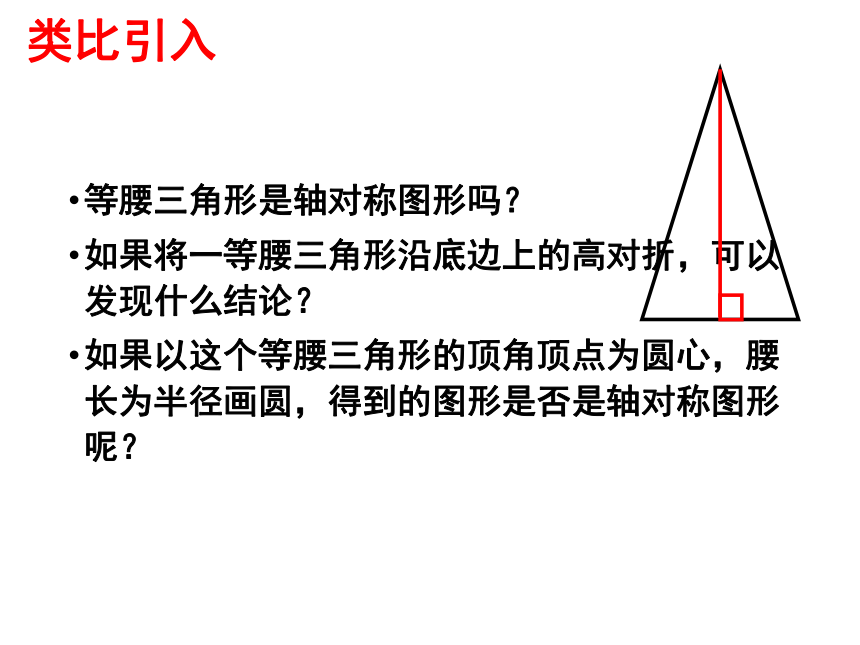
等腰三角形是轴对称图形吗?
如果将一等腰三角形沿底边上的高对折,可以发现什么结论?
如果以这个等腰三角形的顶角顶点为圆心,腰长为半径画圆,得到的图形是否是轴对称图形呢?
类比引入
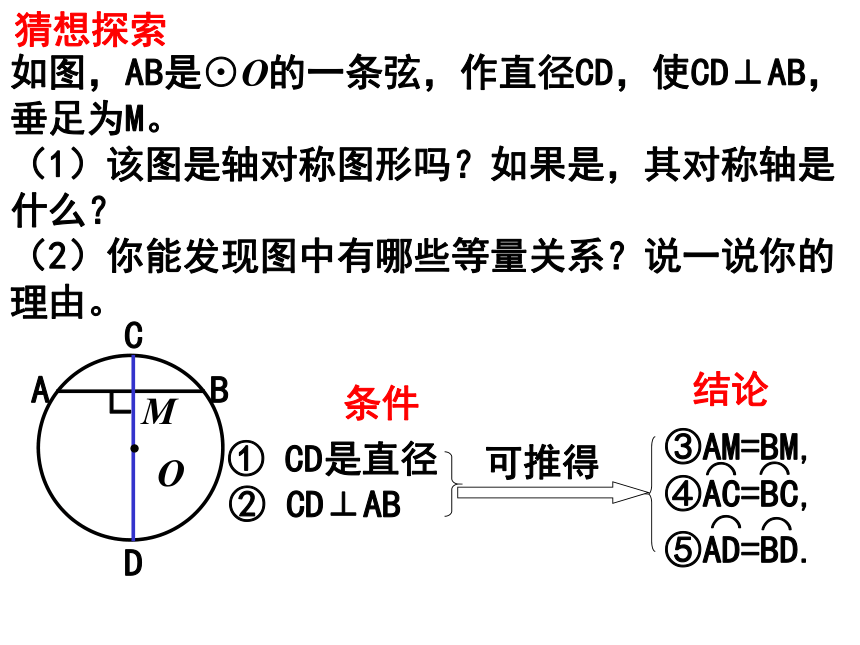
③AM=BM,
① CD是直径
② CD⊥AB
条件
结论
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M。 (1)该图是轴对称图形吗?如果是,其对称轴是什么? (2)你能发现图中有哪些等量关系?说一说你的理由。
猜想探索
证明:连接OA,OB,则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM,∠AOC=∠BOC
∵∠AOD=180°-∠AOC
∠BOD=180°-∠BOC
∴∠AOD=∠BOD
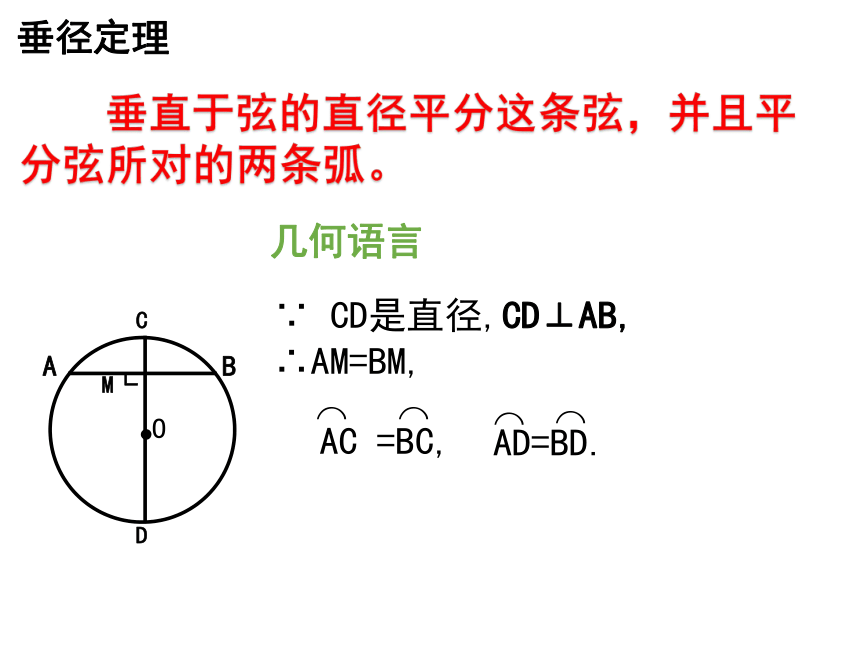
∵ CD是直径,CD⊥AB,
∴AM=BM,
几何语言
垂径定理
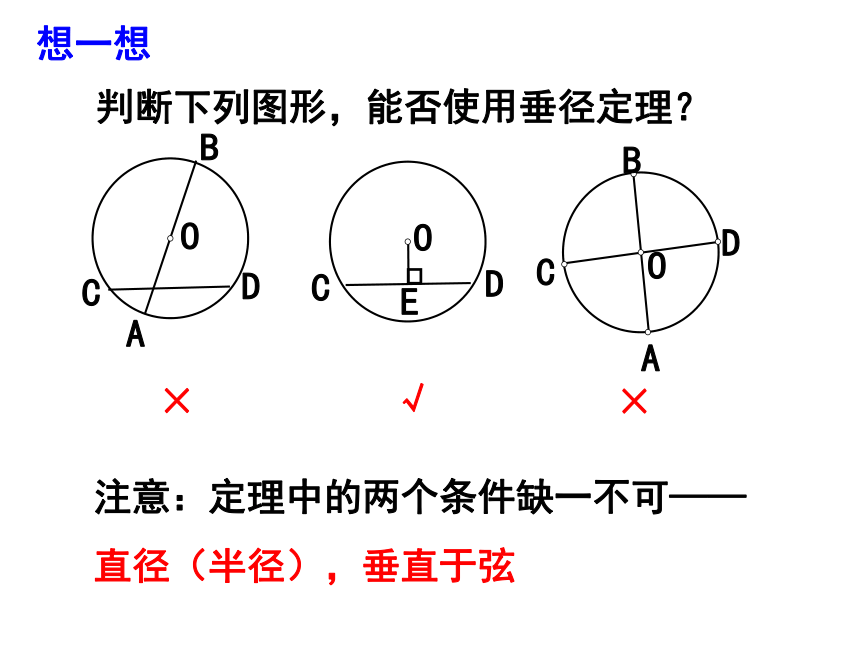
判断下列图形,能否使用垂径定理?
注意:定理中的两个条件缺一不可——
直径(半径),垂直于弦
×
×
√
B
想一想
判断:
1.垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
2.弦的垂直平分线一定平分这条弦所对的弧.
( )
错
对
例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。
则OE=3厘米,AE=BE。∵AB=8厘米 ∴AE=4厘米
在Rt△AOE中,根据勾股定理有OA=5厘米 ∴⊙O的半径为5厘米。
例题1
解:连结OA。过O作OE⊥AB,垂足为E,
例2 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BD
E
例题2
证明:过O作OE⊥AB,垂足为E,
┐
1.如图,⊙O的直径CD
垂直弦AB于点E,且CE=2,DE=8,
则AB的长为( )
A.2 B.4 C.6 D.8
3.如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为____.
知识应用
1、1400年前,我国隋朝建造的赵州石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦长)为37.4米,拱高(即弧的中点到弦的距离)为7.2米,求桥拱所在圆的半径。(结果精确到0.1米)。
随堂练习
2、如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=6cm,OD=4cm,求CD.
随堂练习
D
如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P是EF上任意一点,求PA+PC的最小值.
拓展提升
1.垂径定理.
2、解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连接半径等辅助线,为应用垂径定理创造条件.
归纳小结
第三章 圆
3.3 垂径定理
等腰三角形是轴对称图形吗?
如果将一等腰三角形沿底边上的高对折,可以发现什么结论?
如果以这个等腰三角形的顶角顶点为圆心,腰长为半径画圆,得到的图形是否是轴对称图形呢?
类比引入
③AM=BM,
① CD是直径
② CD⊥AB
条件
结论
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M。 (1)该图是轴对称图形吗?如果是,其对称轴是什么? (2)你能发现图中有哪些等量关系?说一说你的理由。
猜想探索
证明:连接OA,OB,则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM,∠AOC=∠BOC
∵∠AOD=180°-∠AOC
∠BOD=180°-∠BOC
∴∠AOD=∠BOD
∵ CD是直径,CD⊥AB,
∴AM=BM,
几何语言
垂径定理
判断下列图形,能否使用垂径定理?
注意:定理中的两个条件缺一不可——
直径(半径),垂直于弦
×
×
√
B
想一想
判断:
1.垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
2.弦的垂直平分线一定平分这条弦所对的弧.
( )
错
对
例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。
则OE=3厘米,AE=BE。∵AB=8厘米 ∴AE=4厘米
在Rt△AOE中,根据勾股定理有OA=5厘米 ∴⊙O的半径为5厘米。
例题1
解:连结OA。过O作OE⊥AB,垂足为E,
例2 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BD
E
例题2
证明:过O作OE⊥AB,垂足为E,
┐
1.如图,⊙O的直径CD
垂直弦AB于点E,且CE=2,DE=8,
则AB的长为( )
A.2 B.4 C.6 D.8
3.如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为____.
知识应用
1、1400年前,我国隋朝建造的赵州石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦长)为37.4米,拱高(即弧的中点到弦的距离)为7.2米,求桥拱所在圆的半径。(结果精确到0.1米)。
随堂练习
2、如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=6cm,OD=4cm,求CD.
随堂练习
D
如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P是EF上任意一点,求PA+PC的最小值.
拓展提升
1.垂径定理.
2、解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连接半径等辅助线,为应用垂径定理创造条件.
归纳小结
