北师大版九年级数学下册 1.4解直角三角形课件(第1课时 共17张PPT)
文档属性
| 名称 | 北师大版九年级数学下册 1.4解直角三角形课件(第1课时 共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 355.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-13 09:53:23 | ||
图片预览



文档简介
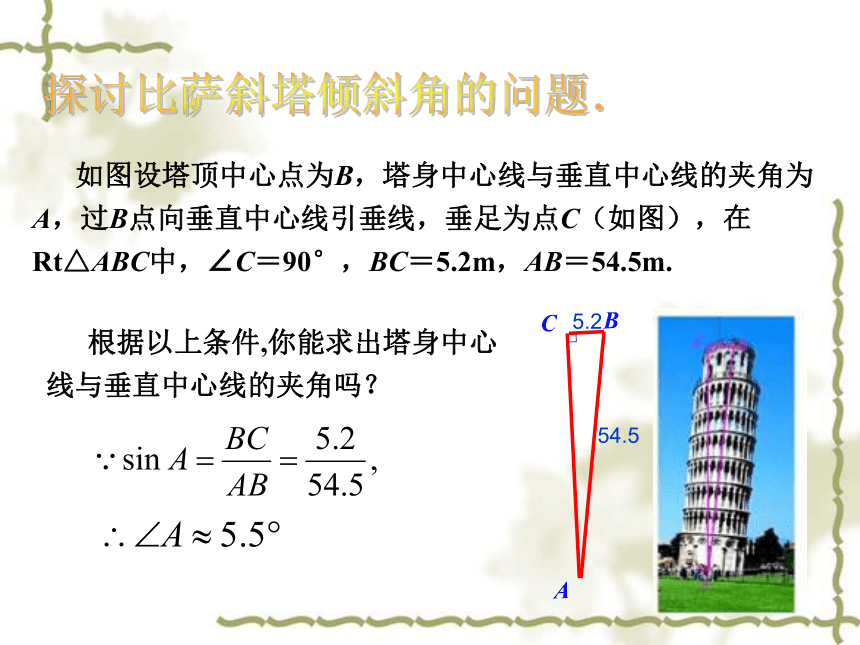
课件17张PPT。解直角三角形(第1课时) 根据以上条件,你能求出塔身中心线与垂直中心线的夹角吗? 如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过B点向垂直中心线引垂线,垂足为点C(如图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.探讨比萨斜塔倾斜角的问题. 5.254.5(2)两锐角之间的关系∠A+∠B=90° (3)边角之间的关系(1)三边之间的关系 (勾股定理)知识回顾思考:利用上面这些关系,必须已知几个元素,才能求得其余元素呢?
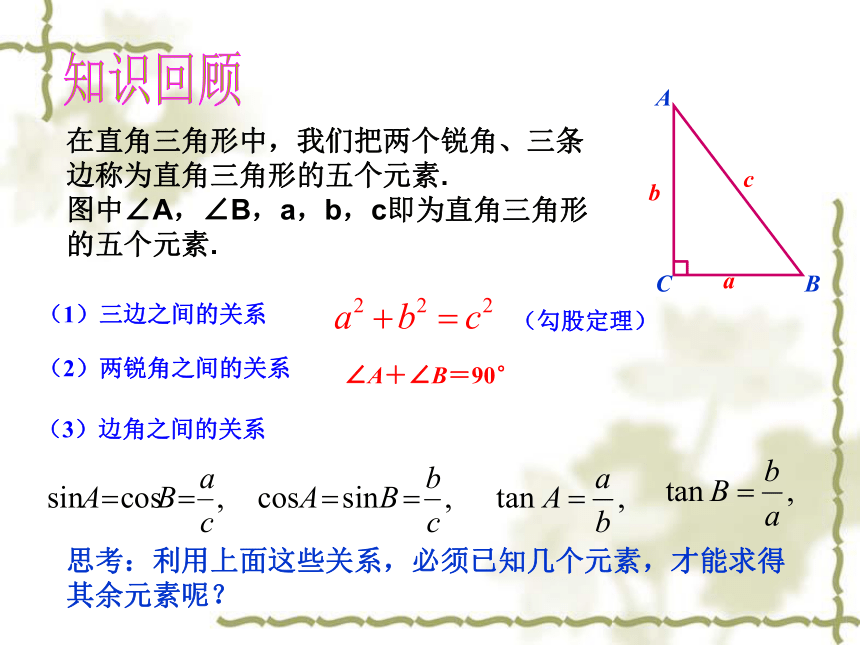
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形
的五个元素.1.在一个直角三角形中,已知一条边和一锐角,或者已知两条边两个元素,才能求出其他元素。
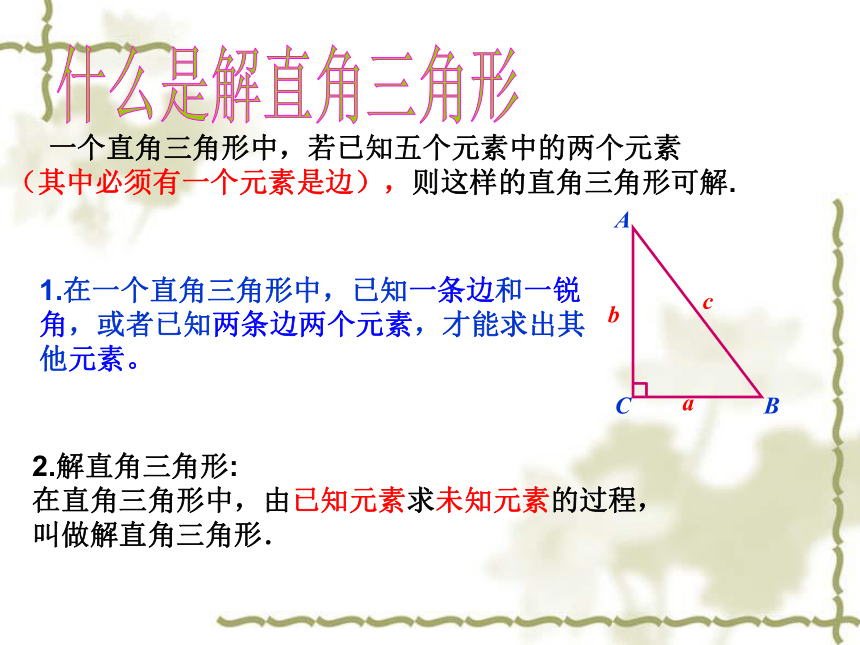
什么是解直角三角形2.解直角三角形:
在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形. 一个直角三角形中,若已知五个元素中的两个元素
(其中必须有一个元素是边),则这样的直角三角形可解.例1 . 如图,在Rt△ABC中,∠C= 90°,
解这个直角三角形.如何解直角三角形解:∵在Rt△ABC中,AC2+BC2=AB2∴AB=∵sinB=∴∠A=60°∴∠B=30°30°例2. 在Rt△ABC中, ∠C=90°, a=35,b=28, 解这个直角三角形.(角的度数精确到1度,c的长 结果保留两位有效数字)如何解直角三角形1.数形结合有利于分析问题;
2.选择关系式时,尽量应用原始数据,使计算更加精确;
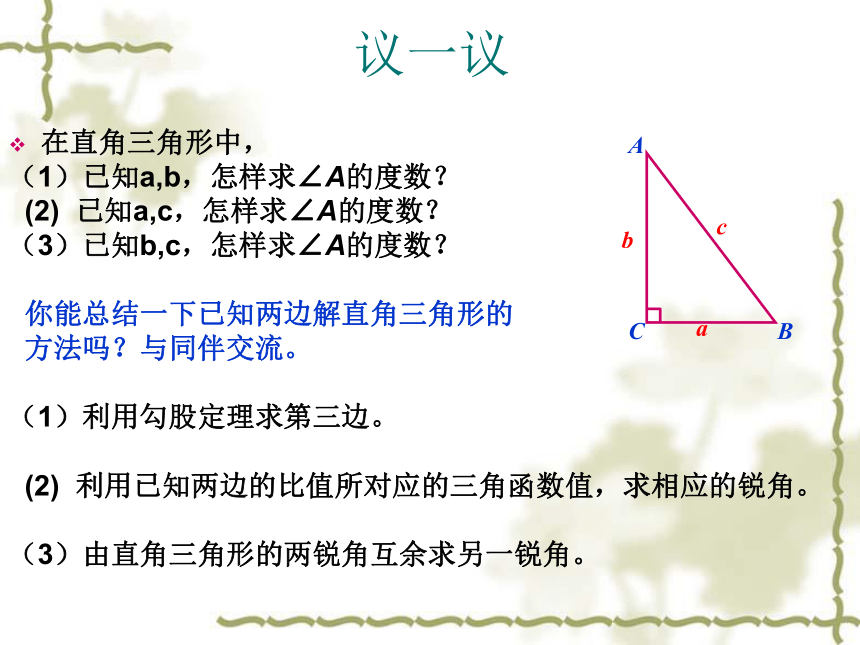
3.解直角三角形时,应求出所有未知元素。议一议在直角三角形中,
(1)已知a,b,怎样求∠A的度数?
(2) 已知a,c,怎样求∠A的度数?
(3)已知b,c,怎样求∠A的度数?
你能总结一下已知两边解直角三角形的
方法吗?与同伴交流。
(1)利用勾股定理求第三边。
(2) 利用已知两边的比值所对应的三角函数值,求相应的锐角。
(3)由直角三角形的两锐角互余求另一锐角。练一练试一试试一试例3 .如图,△ABC中, ∠B=45°, ∠C=30°,
AB=2,求AC的长.解:过A作AD⊥BC于D,
∵ 在Rt △ABD中,∠B=45°,AB=2,45°30°2∴AD=
∵在Rt△ACD中,∠C=30°2×sin45°= 如图,在小岛上有一观察站A.据测,灯塔B在观察站A北偏西450的方向,灯塔C在B正东方向,且相距10海里,灯塔C与观察站A相距10 海里,请你测算灯塔C处在观察站A的什么方向?学以致用1210F 如图,在小岛上有一观察站A.据测,灯塔B在观察站A北偏西450的方向,灯塔C在B正东方向,且相距10海里,灯塔C与观察站A相距10 海里,请你测算灯塔C处在观察站A的什么方向?解:过点C作CD ⊥AB,垂足为D10F∵灯塔B在观察站A北偏西45°的方向∴ ∠B=45°∵sinB =∴CD=BC·sinB=10×sin45°=∵在Rt△DAC中,
sin ∠DAC=∴ ∠ DAC=30°∴∠CAF=∠BAF -∠DAC=45°-30°=15°45°45°∴灯塔C处在观察站A的北偏西15°的方向 如图,在小岛上有一观察站A.据测,灯塔B在观察站A北偏西450的方向,灯塔C在B正东方向,且相距10海里,灯塔C与观察站A相距10 海里,请你测算灯塔C处在观察站A的什么方向?解:过点A作AE⊥BC,垂足为E,10设CE=x∵在Rt△BAE中,∠BAE=45°
∴AE=BE=10+x∵在Rt△CAE中,AE2+CE2=AC2即:x2+10x-50=0(舍去)∴灯塔C处在观察站A的北偏西15° 的方向∴sin ∠CAE=∴∠CAE≈15°45°解直角三角形的知识在生活和生产中有广泛的应用,如在测量高度、距离、角度,确定方案时都常用到解直角三角形。解这类题关键是把实际问题转化为数学问题,常通过作辅助线构造直角三角形来解.温馨提示本节课你学到了什么?作业:《创》P82 [当] 5 A组 1
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形
的五个元素.1.在一个直角三角形中,已知一条边和一锐角,或者已知两条边两个元素,才能求出其他元素。
什么是解直角三角形2.解直角三角形:
在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形. 一个直角三角形中,若已知五个元素中的两个元素
(其中必须有一个元素是边),则这样的直角三角形可解.例1 . 如图,在Rt△ABC中,∠C= 90°,
解这个直角三角形.如何解直角三角形解:∵在Rt△ABC中,AC2+BC2=AB2∴AB=∵sinB=∴∠A=60°∴∠B=30°30°例2. 在Rt△ABC中, ∠C=90°, a=35,b=28, 解这个直角三角形.(角的度数精确到1度,c的长 结果保留两位有效数字)如何解直角三角形1.数形结合有利于分析问题;
2.选择关系式时,尽量应用原始数据,使计算更加精确;
3.解直角三角形时,应求出所有未知元素。议一议在直角三角形中,
(1)已知a,b,怎样求∠A的度数?
(2) 已知a,c,怎样求∠A的度数?
(3)已知b,c,怎样求∠A的度数?
你能总结一下已知两边解直角三角形的
方法吗?与同伴交流。
(1)利用勾股定理求第三边。
(2) 利用已知两边的比值所对应的三角函数值,求相应的锐角。
(3)由直角三角形的两锐角互余求另一锐角。练一练试一试试一试例3 .如图,△ABC中, ∠B=45°, ∠C=30°,
AB=2,求AC的长.解:过A作AD⊥BC于D,
∵ 在Rt △ABD中,∠B=45°,AB=2,45°30°2∴AD=
∵在Rt△ACD中,∠C=30°2×sin45°= 如图,在小岛上有一观察站A.据测,灯塔B在观察站A北偏西450的方向,灯塔C在B正东方向,且相距10海里,灯塔C与观察站A相距10 海里,请你测算灯塔C处在观察站A的什么方向?学以致用1210F 如图,在小岛上有一观察站A.据测,灯塔B在观察站A北偏西450的方向,灯塔C在B正东方向,且相距10海里,灯塔C与观察站A相距10 海里,请你测算灯塔C处在观察站A的什么方向?解:过点C作CD ⊥AB,垂足为D10F∵灯塔B在观察站A北偏西45°的方向∴ ∠B=45°∵sinB =∴CD=BC·sinB=10×sin45°=∵在Rt△DAC中,
sin ∠DAC=∴ ∠ DAC=30°∴∠CAF=∠BAF -∠DAC=45°-30°=15°45°45°∴灯塔C处在观察站A的北偏西15°的方向 如图,在小岛上有一观察站A.据测,灯塔B在观察站A北偏西450的方向,灯塔C在B正东方向,且相距10海里,灯塔C与观察站A相距10 海里,请你测算灯塔C处在观察站A的什么方向?解:过点A作AE⊥BC,垂足为E,10设CE=x∵在Rt△BAE中,∠BAE=45°
∴AE=BE=10+x∵在Rt△CAE中,AE2+CE2=AC2即:x2+10x-50=0(舍去)∴灯塔C处在观察站A的北偏西15° 的方向∴sin ∠CAE=∴∠CAE≈15°45°解直角三角形的知识在生活和生产中有广泛的应用,如在测量高度、距离、角度,确定方案时都常用到解直角三角形。解这类题关键是把实际问题转化为数学问题,常通过作辅助线构造直角三角形来解.温馨提示本节课你学到了什么?作业:《创》P82 [当] 5 A组 1
