人教版数学八年级上册:14.3.1 因式分解——提公因式法 教案
文档属性
| 名称 | 人教版数学八年级上册:14.3.1 因式分解——提公因式法 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 36.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-13 00:00:00 | ||
图片预览

文档简介
课题名称:14.3.1 因式分解——提公因式法
年级学科 八年级数学 教材版本 人教版
一、教学内容分析
因式分解是代数式中的重要内容,它与前一章整式和后一章分式联系极为密切。因式分解的教学是在整式四则运算的基础上进行的,因式分解方法的理论依据就是多项式乘法的逆变形。它不仅在多项式的除法、简便运算中有直接的应用,也为以后学习分式、解方程(组)及三角函数式的恒等变形提供了必要的基础。因此,学好因式分解对于代数知识的后续学习,具有相当重要的意义。 提公因式法是因式分解的基本方法。通过逆向运用分配律,将多项式中各项的公因式提到括号外边,从而把多项式分解为此公因式与多项式剩余部分所组成的因式的积。其中,公因式可以是单项式,也可以是数或多项式。
二、教学目标
1、了解因式分解的概念。 2、了解公因式的概念,能用提公因式法进行因式分解。 重点:运用提公因式法分解因式。 难点:理解因式分解与整式乘法的相互关系,准确找出公因式。
三、学习者特征分析
因式分解不同于数的计算,是对整式的变形,学生初次接触在理解上会有一定的困难。在对整式乘法的认识还不够深入的情况下,遇到与之有互逆关系的情景,会茫然甚至出现反转回去做乘法的错误。在学生预习时,要设计整式乘法题目和乘法分配律运用的题目。
四、教学过程
本教学是按“简算——感知——概括——巩固、应用和拓展”的模式呈现教学内容的,引导学生体会知识的发生发展过程,这种呈现方式符合八年级学生的认知规律和学习规律,使学生从被动的学习到主动探索和发现的转化中感受到学习与探索的乐趣。
五、教学设计
教师活动 预设学生活动 设计意图
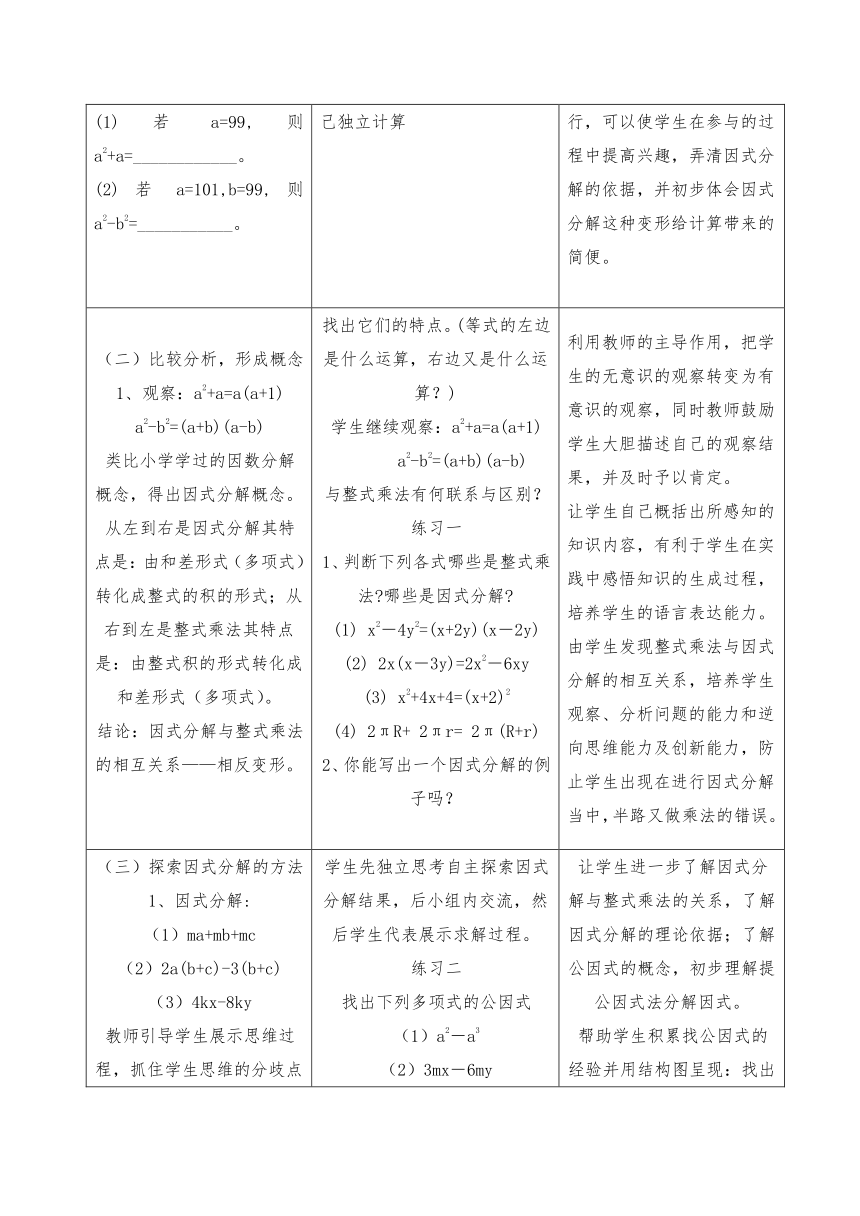
看谁算得快: (1)若a=99,则a2+a=____________。 (2)若a=101,b=99,则a2-b2=___________。 学生应用前面学过知识自己独立计算 情境导入借助抢答的方式进行,可以使学生在参与的过程中提高兴趣,弄清因式分解的依据,并初步体会因式分解这种变形给计算带来的简便。
(二)比较分析,形成概念 1、观察:a2+a=a(a+1) a2-b2=(a+b)(a-b) 类比小学学过的因数分解概念,得出因式分解概念。 从左到右是因式分解其特点是:由和差形式(多项式)转化成整式的积的形式;从右到左是整式乘法其特点是:由整式积的形式转化成和差形式(多项式)。 结论:因式分解与整式乘法的相互关系——相反变形。 找出它们的特点。(等式的左边是什么运算,右边又是什么运算?) 学生继续观察:a2+a=a(a+1) a2-b2=(a+b)(a-b) 与整式乘法有何联系与区别? 练习一 1、判断下列各式哪些是整式乘法?哪些是因式分解? (1) x2-4y2=(x+2y)(x-2y) (2) 2x(x-3y)=2x2-6xy (3) x2+4x+4=(x+2)2(4) 2πR+ 2πr= 2π(R+r) 2、你能写出一个因式分解的例子吗? 利用教师的主导作用,把学生的无意识的观察转变为有意识的观察,同时教师鼓励学生大胆描述自己的观察结果,并及时予以肯定。 让学生自己概括出所感知的知识内容,有利于学生在实践中感悟知识的生成过程,培养学生的语言表达能力。 由学生发现整式乘法与因式分解的相互关系,培养学生观察、分析问题的能力和逆向思维能力及创新能力,防止学生出现在进行因式分解当中,半路又做乘法的错误。
(三)探索因式分解的方法 1、因式分解: (1)ma+mb+mc (2)2a(b+c)-3(b+c) (3)4kx-8ky 教师引导学生展示思维过程,抓住学生思维的分歧点和错误充分讨论,让学生明确公因式的意义及提公因式法。 公因式:多项式中各项都有的因式,叫做这个多项式的公因式。 提公因式法:把多项式写成公因式与另一个因式的积的形式,这种因式分解的方式叫提公因式法。 学生先独立思考自主探索因式分解结果,后小组内交流,然后学生代表展示求解过程。 练习二 找出下列多项式的公因式 (1)a2-a3(2)3mx-6my (3)p(a2+b2)-q(a2+b2) (4)a2b-2ab2+ab (5)12xyz-9x2y2 让学生进一步了解因式分解与整式乘法的关系,了解因式分解的理论依据;了解公因式的概念,初步理解提公因式法分解因式。 帮助学生积累找公因式的经验并用结构图呈现:找出多项式各项系数的最大公因数和各项都含有的字母及多项式的最低次幂的乘积。
(四)初步应用提公因式法 例1 分解因式 8a3b2+12ab3c 例2 分解因式 2a(y-z)-3b(z-y) 课堂回顾 今天这节课,你学到了哪些知识?有哪些收获与感受?说出来大家分享。 练习三 1、 把下列各式分解因式 (1)7am+14a2 m (2)24x3y-18x2y (3)4a2(x+7)-3(x+7) (4)x(x-1)+(1-x) 2、当a=3.14,b=2.386,c=1.386时,求ab-ac的值. 引导学生了解提公因式法分解因式的基本步骤,用提公因式法分解因式后,应保证多项式的因式中再无公因式。 通过一组练习让学生巩固提公因式法分解因式的步骤,引导学生反思检验因式分解是否正确,只要看等式右边几个整式相乘的积与右边的多项式是否相等。 课堂小结交给学生,让学生总结本节课中概念的发现过程,运用概念分析问题的过程,养成学生学习——反思——学习的良好习惯。唯有总结反思,才能促进理解,提高认知水平,从而促进数学观点的形成和发展,更好地进行知识建构,实现良性循环。
六、教学板书
14.3.1 提公因式法 1、因式分解 例: 练习: 2、提公因式法 例:
年级学科 八年级数学 教材版本 人教版
一、教学内容分析
因式分解是代数式中的重要内容,它与前一章整式和后一章分式联系极为密切。因式分解的教学是在整式四则运算的基础上进行的,因式分解方法的理论依据就是多项式乘法的逆变形。它不仅在多项式的除法、简便运算中有直接的应用,也为以后学习分式、解方程(组)及三角函数式的恒等变形提供了必要的基础。因此,学好因式分解对于代数知识的后续学习,具有相当重要的意义。 提公因式法是因式分解的基本方法。通过逆向运用分配律,将多项式中各项的公因式提到括号外边,从而把多项式分解为此公因式与多项式剩余部分所组成的因式的积。其中,公因式可以是单项式,也可以是数或多项式。
二、教学目标
1、了解因式分解的概念。 2、了解公因式的概念,能用提公因式法进行因式分解。 重点:运用提公因式法分解因式。 难点:理解因式分解与整式乘法的相互关系,准确找出公因式。
三、学习者特征分析
因式分解不同于数的计算,是对整式的变形,学生初次接触在理解上会有一定的困难。在对整式乘法的认识还不够深入的情况下,遇到与之有互逆关系的情景,会茫然甚至出现反转回去做乘法的错误。在学生预习时,要设计整式乘法题目和乘法分配律运用的题目。
四、教学过程
本教学是按“简算——感知——概括——巩固、应用和拓展”的模式呈现教学内容的,引导学生体会知识的发生发展过程,这种呈现方式符合八年级学生的认知规律和学习规律,使学生从被动的学习到主动探索和发现的转化中感受到学习与探索的乐趣。
五、教学设计
教师活动 预设学生活动 设计意图
看谁算得快: (1)若a=99,则a2+a=____________。 (2)若a=101,b=99,则a2-b2=___________。 学生应用前面学过知识自己独立计算 情境导入借助抢答的方式进行,可以使学生在参与的过程中提高兴趣,弄清因式分解的依据,并初步体会因式分解这种变形给计算带来的简便。
(二)比较分析,形成概念 1、观察:a2+a=a(a+1) a2-b2=(a+b)(a-b) 类比小学学过的因数分解概念,得出因式分解概念。 从左到右是因式分解其特点是:由和差形式(多项式)转化成整式的积的形式;从右到左是整式乘法其特点是:由整式积的形式转化成和差形式(多项式)。 结论:因式分解与整式乘法的相互关系——相反变形。 找出它们的特点。(等式的左边是什么运算,右边又是什么运算?) 学生继续观察:a2+a=a(a+1) a2-b2=(a+b)(a-b) 与整式乘法有何联系与区别? 练习一 1、判断下列各式哪些是整式乘法?哪些是因式分解? (1) x2-4y2=(x+2y)(x-2y) (2) 2x(x-3y)=2x2-6xy (3) x2+4x+4=(x+2)2(4) 2πR+ 2πr= 2π(R+r) 2、你能写出一个因式分解的例子吗? 利用教师的主导作用,把学生的无意识的观察转变为有意识的观察,同时教师鼓励学生大胆描述自己的观察结果,并及时予以肯定。 让学生自己概括出所感知的知识内容,有利于学生在实践中感悟知识的生成过程,培养学生的语言表达能力。 由学生发现整式乘法与因式分解的相互关系,培养学生观察、分析问题的能力和逆向思维能力及创新能力,防止学生出现在进行因式分解当中,半路又做乘法的错误。
(三)探索因式分解的方法 1、因式分解: (1)ma+mb+mc (2)2a(b+c)-3(b+c) (3)4kx-8ky 教师引导学生展示思维过程,抓住学生思维的分歧点和错误充分讨论,让学生明确公因式的意义及提公因式法。 公因式:多项式中各项都有的因式,叫做这个多项式的公因式。 提公因式法:把多项式写成公因式与另一个因式的积的形式,这种因式分解的方式叫提公因式法。 学生先独立思考自主探索因式分解结果,后小组内交流,然后学生代表展示求解过程。 练习二 找出下列多项式的公因式 (1)a2-a3(2)3mx-6my (3)p(a2+b2)-q(a2+b2) (4)a2b-2ab2+ab (5)12xyz-9x2y2 让学生进一步了解因式分解与整式乘法的关系,了解因式分解的理论依据;了解公因式的概念,初步理解提公因式法分解因式。 帮助学生积累找公因式的经验并用结构图呈现:找出多项式各项系数的最大公因数和各项都含有的字母及多项式的最低次幂的乘积。
(四)初步应用提公因式法 例1 分解因式 8a3b2+12ab3c 例2 分解因式 2a(y-z)-3b(z-y) 课堂回顾 今天这节课,你学到了哪些知识?有哪些收获与感受?说出来大家分享。 练习三 1、 把下列各式分解因式 (1)7am+14a2 m (2)24x3y-18x2y (3)4a2(x+7)-3(x+7) (4)x(x-1)+(1-x) 2、当a=3.14,b=2.386,c=1.386时,求ab-ac的值. 引导学生了解提公因式法分解因式的基本步骤,用提公因式法分解因式后,应保证多项式的因式中再无公因式。 通过一组练习让学生巩固提公因式法分解因式的步骤,引导学生反思检验因式分解是否正确,只要看等式右边几个整式相乘的积与右边的多项式是否相等。 课堂小结交给学生,让学生总结本节课中概念的发现过程,运用概念分析问题的过程,养成学生学习——反思——学习的良好习惯。唯有总结反思,才能促进理解,提高认知水平,从而促进数学观点的形成和发展,更好地进行知识建构,实现良性循环。
六、教学板书
14.3.1 提公因式法 1、因式分解 例: 练习: 2、提公因式法 例:
