人教版数学七年级下册:5.3.1 平行线的性质 教案
文档属性
| 名称 | 人教版数学七年级下册:5.3.1 平行线的性质 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 45.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-13 10:01:10 | ||
图片预览

文档简介
课题名称:平行线的性质
年级学科 初二数学 教材版本 人教版
一、教学内容分析
本节课内容是人教版七年级下册第五章内容,在前两节课我们已经学习了平行线的判定及性质。了解到研究平行线与两条直线被第三条直线所截形成的角之间的关系,为本节内容打下了基础,在学习本节中,学生在经历探索和交流的活动中,加深了对平行线的理解,进一步发展学生的空间观念,为以后的几何推理、证明起重要作用
二、教学目标
(1)平行线的性质与判定的应用.
(2)经历例题的分析过程,从中体会转化的思想和分析问题的方法,进一步培养推理能力,体会数学在实际生活中的应用.
三、学习者特征分析
本节课本着“在做中学”的理念,特制订以下教法学法
(1)改变学生的学习方式,让学生合作学习,培养学生的合作精神
(2)发挥学生的观察力,联想力,将所学知识加以简单应用,使知识达到“融会贯通”,培养学生“学以致用”的意识。
(3)鼓励学生大胆猜想,发挥能动性,积极参与探索,培养思维的严密性
四、教学过程
梳理旧知,引入新课 问题1 (1)平行线的性质是什么? 性质1 两直线平行,同位角相等 性质2 两直线平行,内错角相等 性质3 两直线平行,同旁内角互补 (2)结合图形回答问题:
①如果AB∥CD ,∠1与∠2相等吗?为什么? 答:相等.根据两直线平行,内错角相等.
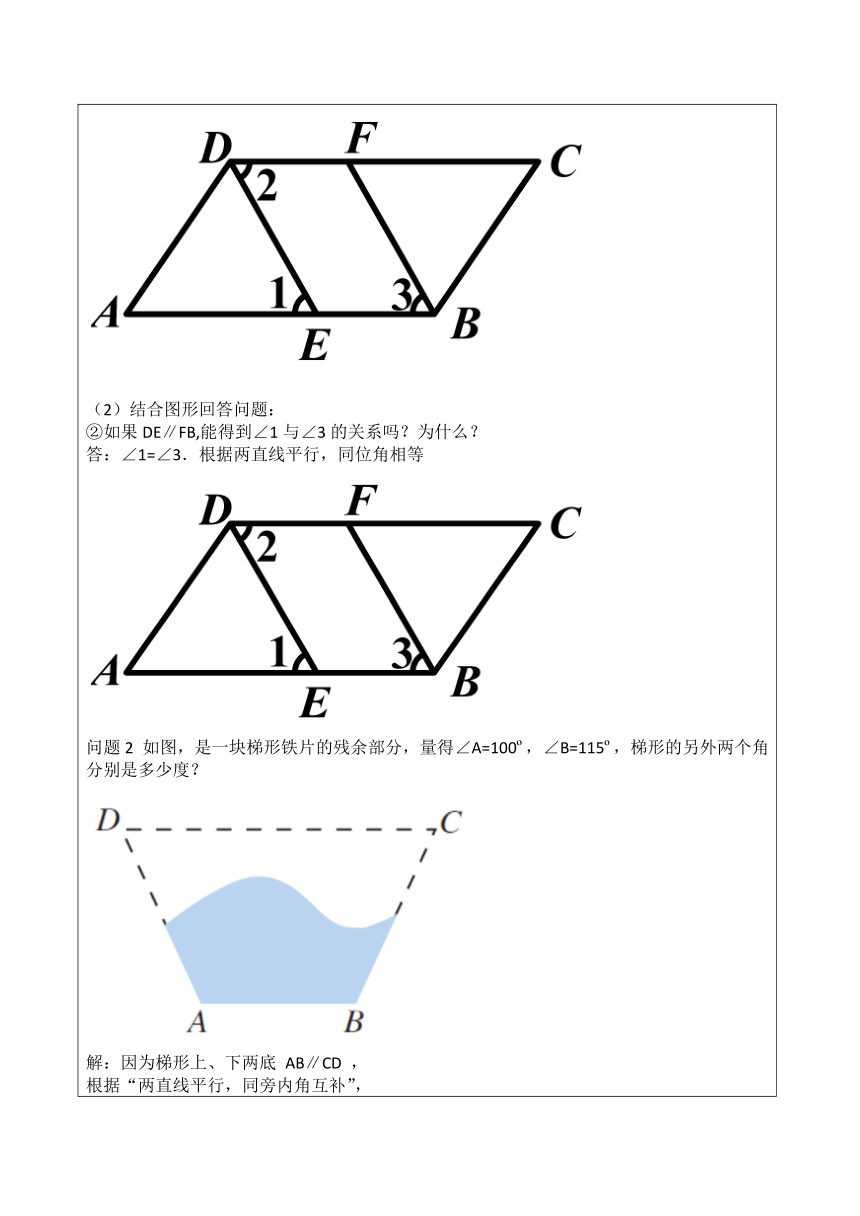
(2)结合图形回答问题: ②如果DE∥FB,能得到∠1与∠3的关系吗?为什么? 答:∠1=∠3.根据两直线平行,同位角相等 问题2 如图,是一块梯形铁片的残余部分,量得∠A=100?,∠B=115?,梯形的另外两个角分别是多少度?
解:因为梯形上、下两底 AB∥CD ,
根据“两直线平行,同旁内角互补”,
可得∠A+∠D =180?,∠B+∠C =180?.
于是∠D =180?-∠A
=180?-100?o =80? ,
∠C =180?-∠B
=180?-115? =65? .
所以,梯形的另外两个角分别是80?,65? . 问题3 对比平行线的性质和判定方法,你能说出它们的区别吗?
学生作答 教师以幻灯片呈现 问题4 已知,如图,∠1=∠2,CE∥BF,
试说明: AB∥CD.
理由如下:
∵ CE∥BF,
∴∠1=∠B.
∵∠1=∠2 ,
∴∠2=∠B.
∵∠2和∠B是内错角,
∴ AB∥CD(内错角相等,两直线平行). 综合运用,巩固提高 练习1 如图,AB∥CD,BE平分∠ABC,CF平分
∠BCD,你能发现BE与CF的位置关系吗?说明理由 理由如下:
∵ BE平分∠ABC,
∴
同理
∵ AB∥CD,
∴∠ABC=∠BCD.
∴∠1=∠2.
∵∠1和∠2是内错角,
∴ BE∥CF(内错角相等,两直线平行) 归纳小结 (1)平行线的性质与判定的区别是什么? (2)在解决具体问题过程中,你能区别什么时候需要使用平行线的性质,什么时候需要使用平行线的判定吗? 4.课堂练习 5.布置作业 教科书 习题5.3 第7、8、题
五、教学板书(本节课的教学板书)
平行线性质 性质 根据图形回答 归纳小结 性质1 两直线平行,同位角相等 性质2 两直线平行,内错角相等 性质3 两直线平行,同旁内角互补
年级学科 初二数学 教材版本 人教版
一、教学内容分析
本节课内容是人教版七年级下册第五章内容,在前两节课我们已经学习了平行线的判定及性质。了解到研究平行线与两条直线被第三条直线所截形成的角之间的关系,为本节内容打下了基础,在学习本节中,学生在经历探索和交流的活动中,加深了对平行线的理解,进一步发展学生的空间观念,为以后的几何推理、证明起重要作用
二、教学目标
(1)平行线的性质与判定的应用.
(2)经历例题的分析过程,从中体会转化的思想和分析问题的方法,进一步培养推理能力,体会数学在实际生活中的应用.
三、学习者特征分析
本节课本着“在做中学”的理念,特制订以下教法学法
(1)改变学生的学习方式,让学生合作学习,培养学生的合作精神
(2)发挥学生的观察力,联想力,将所学知识加以简单应用,使知识达到“融会贯通”,培养学生“学以致用”的意识。
(3)鼓励学生大胆猜想,发挥能动性,积极参与探索,培养思维的严密性
四、教学过程
梳理旧知,引入新课 问题1 (1)平行线的性质是什么? 性质1 两直线平行,同位角相等 性质2 两直线平行,内错角相等 性质3 两直线平行,同旁内角互补 (2)结合图形回答问题:
①如果AB∥CD ,∠1与∠2相等吗?为什么? 答:相等.根据两直线平行,内错角相等.
(2)结合图形回答问题: ②如果DE∥FB,能得到∠1与∠3的关系吗?为什么? 答:∠1=∠3.根据两直线平行,同位角相等 问题2 如图,是一块梯形铁片的残余部分,量得∠A=100?,∠B=115?,梯形的另外两个角分别是多少度?
解:因为梯形上、下两底 AB∥CD ,
根据“两直线平行,同旁内角互补”,
可得∠A+∠D =180?,∠B+∠C =180?.
于是∠D =180?-∠A
=180?-100?o =80? ,
∠C =180?-∠B
=180?-115? =65? .
所以,梯形的另外两个角分别是80?,65? . 问题3 对比平行线的性质和判定方法,你能说出它们的区别吗?
学生作答 教师以幻灯片呈现 问题4 已知,如图,∠1=∠2,CE∥BF,
试说明: AB∥CD.
理由如下:
∵ CE∥BF,
∴∠1=∠B.
∵∠1=∠2 ,
∴∠2=∠B.
∵∠2和∠B是内错角,
∴ AB∥CD(内错角相等,两直线平行). 综合运用,巩固提高 练习1 如图,AB∥CD,BE平分∠ABC,CF平分
∠BCD,你能发现BE与CF的位置关系吗?说明理由 理由如下:
∵ BE平分∠ABC,
∴
同理
∵ AB∥CD,
∴∠ABC=∠BCD.
∴∠1=∠2.
∵∠1和∠2是内错角,
∴ BE∥CF(内错角相等,两直线平行) 归纳小结 (1)平行线的性质与判定的区别是什么? (2)在解决具体问题过程中,你能区别什么时候需要使用平行线的性质,什么时候需要使用平行线的判定吗? 4.课堂练习 5.布置作业 教科书 习题5.3 第7、8、题
五、教学板书(本节课的教学板书)
平行线性质 性质 根据图形回答 归纳小结 性质1 两直线平行,同位角相等 性质2 两直线平行,内错角相等 性质3 两直线平行,同旁内角互补
