1.2.2基本初等函数的导数公式及导数的运算法则(共41张PPT)
文档属性
| 名称 | 1.2.2基本初等函数的导数公式及导数的运算法则(共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 22:29:58 | ||
图片预览


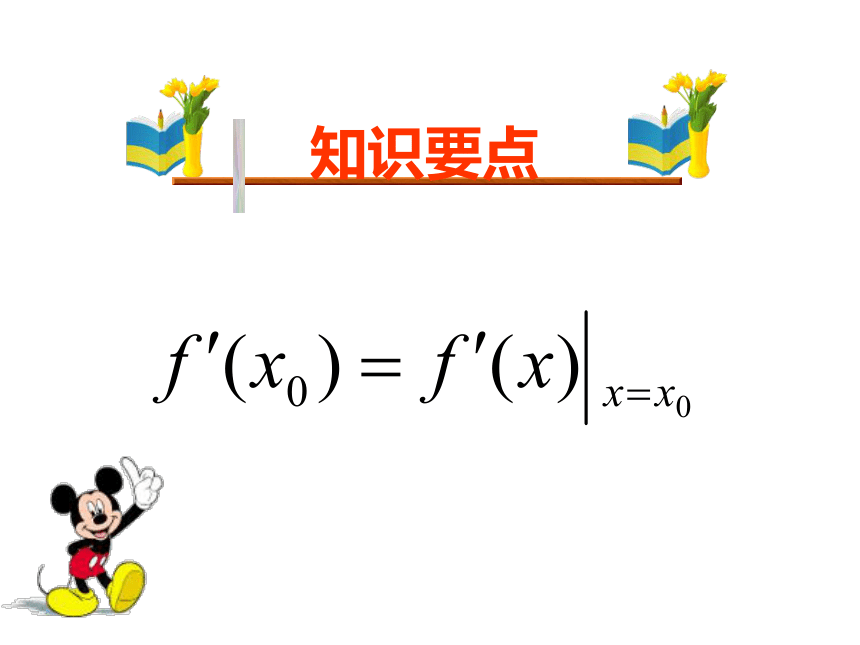









文档简介
(共41张PPT)
3.2.2 基本初等函数的导数公式及导数的运算法则
旧知回顾
求函数的导数的方法是:
(1)求增量
(2)算比值
(3)求极限
知识要点
新课导入
由上节课的内容可知函数y=x2的导数为y’=2x,那么,于一般的二次函数y=ax2+bx+c,它的导数又是什么呢?这就需要用到函数的四则运算的求导法则.
又如我们知道函数y=1/x2的导数是 =-2/x3,那么函数y=1/(3x-2)2的导数又是什么呢?
学习了这节课,就可以解决这些问题了!
为了方便,今后我们可以直接使用下面的初等函数的导数公式表:
基本初等函数的导数公式
这些都记住了吗?
解:根据基本初等函数的导数公式表,有
因此,在第10个年头,这种商品的价格约以0.08元/年的速度上涨.
若u=u(x),v=v(x)在x处可导,则
根据导数的定义,可以推出可导函数四则运算的求导法则
1.和(或差)的导数
法则1 两个函数的和(或差)的导数,等于这两个函数的导数的和(或差),即
1.和(或差)的导数
解:由导数的基本公式得:
解:由导数的基本公式得:
2.积的导数
法则2 两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数,即
请同学们自己证明
解:由导数的基本公式得:
解:由导数的基本公式得:
3.商的导数
法则3 两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方,即
导数的运算法则
1. [f(x) ±g(x)] ′=f′(x) ±g(x) ′;
2. [f(x) .g(x)] ′=f′(x) g(x)± f(x) g(x) ′;
如何求函数y=㏑(x+2)的函数呢?
我们无法用现有的方法求函数y=㏑(x+2)的导数.下面,我们先分析这个函数的结构特点.
若设u=x+2(x>-2),则y=ln u.即y=㏑(x+2)可以看成是由y=ln u和u=x+2(x>-2)经过“复合”得到的,即y可以通过中间变量u表示为自变量x的函数.
一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数.记做y=f(g(x)).
即y对x的导数等于y对u的导数与u对x的导数的乘积.
由此可得,y=㏑(3x+2)对x的导数等于y= ㏑u对u的导数与u=3x+2对x的导数的乘积,即
课堂小结
1. 由常函数、幂函数及正、余弦函数经加、减、乘运算得到的简单的函数均可利用求导法则与导数公式求导,而不需要回到导数的定义去求此类简单函数的导数 .
2.导数的运算法则
1. [f(x) ±g(x)] ′=f′(x) ±g(x) ′
2. [f(x) .g(x)] ′=f′(x) g(x)± f(x) g(x) ′
3.复合函数的复合过程
利用复合函数的求导法则来求导数时,选择中间变量是复合函数求导的关键.
高考链接
(2018海南文)设 ,若
,则 ( )
A. B.
C. D.
B
(2018全国Ⅱ卷文)设曲线
在点(1, )
处的切线与直线
平行,则
A.1 B.
C.
D.
( )
A
随堂练习
随堂练习
2、 求下列函数的导数
3.2.2 基本初等函数的导数公式及导数的运算法则
旧知回顾
求函数的导数的方法是:
(1)求增量
(2)算比值
(3)求极限
知识要点
新课导入
由上节课的内容可知函数y=x2的导数为y’=2x,那么,于一般的二次函数y=ax2+bx+c,它的导数又是什么呢?这就需要用到函数的四则运算的求导法则.
又如我们知道函数y=1/x2的导数是 =-2/x3,那么函数y=1/(3x-2)2的导数又是什么呢?
学习了这节课,就可以解决这些问题了!
为了方便,今后我们可以直接使用下面的初等函数的导数公式表:
基本初等函数的导数公式
这些都记住了吗?
解:根据基本初等函数的导数公式表,有
因此,在第10个年头,这种商品的价格约以0.08元/年的速度上涨.
若u=u(x),v=v(x)在x处可导,则
根据导数的定义,可以推出可导函数四则运算的求导法则
1.和(或差)的导数
法则1 两个函数的和(或差)的导数,等于这两个函数的导数的和(或差),即
1.和(或差)的导数
解:由导数的基本公式得:
解:由导数的基本公式得:
2.积的导数
法则2 两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数,即
请同学们自己证明
解:由导数的基本公式得:
解:由导数的基本公式得:
3.商的导数
法则3 两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方,即
导数的运算法则
1. [f(x) ±g(x)] ′=f′(x) ±g(x) ′;
2. [f(x) .g(x)] ′=f′(x) g(x)± f(x) g(x) ′;
如何求函数y=㏑(x+2)的函数呢?
我们无法用现有的方法求函数y=㏑(x+2)的导数.下面,我们先分析这个函数的结构特点.
若设u=x+2(x>-2),则y=ln u.即y=㏑(x+2)可以看成是由y=ln u和u=x+2(x>-2)经过“复合”得到的,即y可以通过中间变量u表示为自变量x的函数.
一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数.记做y=f(g(x)).
即y对x的导数等于y对u的导数与u对x的导数的乘积.
由此可得,y=㏑(3x+2)对x的导数等于y= ㏑u对u的导数与u=3x+2对x的导数的乘积,即
课堂小结
1. 由常函数、幂函数及正、余弦函数经加、减、乘运算得到的简单的函数均可利用求导法则与导数公式求导,而不需要回到导数的定义去求此类简单函数的导数 .
2.导数的运算法则
1. [f(x) ±g(x)] ′=f′(x) ±g(x) ′
2. [f(x) .g(x)] ′=f′(x) g(x)± f(x) g(x) ′
3.复合函数的复合过程
利用复合函数的求导法则来求导数时,选择中间变量是复合函数求导的关键.
高考链接
(2018海南文)设 ,若
,则 ( )
A. B.
C. D.
B
(2018全国Ⅱ卷文)设曲线
在点(1, )
处的切线与直线
平行,则
A.1 B.
C.
D.
( )
A
随堂练习
随堂练习
2、 求下列函数的导数
