华师大版八年级数学下册第十六章16.1.1分式的概念课件(共22张PPT)
文档属性
| 名称 | 华师大版八年级数学下册第十六章16.1.1分式的概念课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 488.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-13 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
某同学x分钟做了60个仰卧起坐,他每分钟做多少个?
这个式子是不是整式?
回忆一下,什么是整式?
七年级的时候我们大家都学习过整式,有谁记得整式的概念吗?
整 式:
单项式和多项式统称整式。
单项式:
多项式:
数和字母的乘积叫做单项式,单独一个数或一个字母也是单项式
几个单项式的和。
知识要点:
1.分式的概念
2.分式有意义的条件
3.分式值为零的条件
做一做:
(1)面积为2平方米的长方形一边长3米,则它
的另一边长为________米;
(2)面积为S平方米的长方形一边长a米,则它
的另一边长为________米;
(3)一箱苹果售价p元,总重m千克,箱重n千克,
则每千克苹果的售价是____________元.
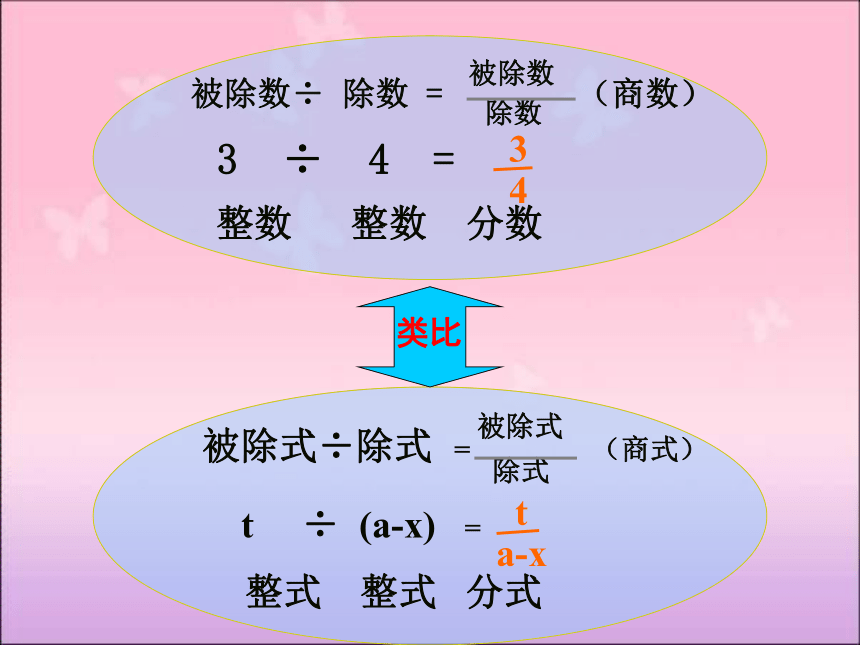
分式的概念:
用A、B表示两个整式,A÷B就可以
表示成 形式。如果B中含有字母,B≠0,
式子 就叫做分式。其中,A叫做分式的
分子,B叫做分式的分母。
分式的特征是: ①分子、分母 是 ;
②分母中含有 。
字母
都
整式
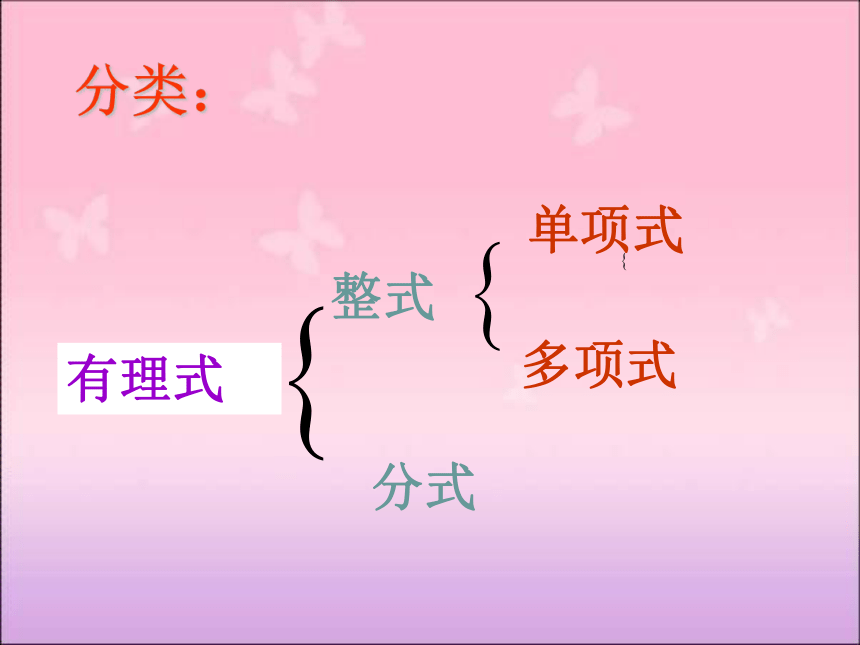
分式
有理式
整式
单项式
多项式
分类:
例1:下列式子中哪些是整式,哪些是分式?
整式:(1),(4),(6),(7),(8)
分式:(2),(3),(5)
区分整式与分式的关键是看分母,分母中含有字母的是分式,不含字母的是整式。
练习1:
把下列各式的题号分别填入表中
(2)(3)(5)
(1)(4)(6)(7)
(1)(2)(3)(4)(5)(6)(7)
整 式 分 式 有 理 式
探索与发现(求代数式的值)
0
-1
0
0
-1
-1
-1
思考:
1、第2个分式在什么情况下无意义?
2、 这三个分式在什么情况下有意义?
3、这三个分式在什么情况下值为零?
无意义
无意义
x … -2 -1 0 1 2 …
… …
… …
… …
归纳:
对于分式
(1)分式无意义的条件是 。
(2)分式有意义的条件是 。
(3)分式的值为零的条件是 。
B=0
B≠0
A=0且B≠0
(分母为零)
(分母不为零)
(分子为零且分母不为零)
例2:当 取什么值时,下列分式有意义?
分 析
要使分式有意义,必须且只须分母不等于零。
解:
练习2
当 取何值时,下列分式有意义。
分 析
分式有意义的条件是分母不等于零。
例3:当 是什么数时,下列分式的值 为零?
3、当a取什么值时,分式 有意义。
练习3:
学以致用
求:当 1.分式的值为正时x的范围;
2.分式的值为负时x的范围.
谈一谈这一节课的收获和体会 。
①分子分母都是整式
②分母中必含有字母
分母中字母的取值不能使分母值为零,否则分式无意义
当分子为零且分母不为零时,分式值为零。
分式的概念
小测
1、(1)在下面四个有理式中,分式为( )(15分)
⑵
A、 B、 C、 D、- +
当x=-1时,下列分式没有意义的是( ) (15分)
A、 B、 C、 D、
2、⑴
⑵
某同学x分钟做了60个仰卧起坐,他每分钟做多少个?
这个式子是不是整式?
回忆一下,什么是整式?
七年级的时候我们大家都学习过整式,有谁记得整式的概念吗?
整 式:
单项式和多项式统称整式。
单项式:
多项式:
数和字母的乘积叫做单项式,单独一个数或一个字母也是单项式
几个单项式的和。
知识要点:
1.分式的概念
2.分式有意义的条件
3.分式值为零的条件
做一做:
(1)面积为2平方米的长方形一边长3米,则它
的另一边长为________米;
(2)面积为S平方米的长方形一边长a米,则它
的另一边长为________米;
(3)一箱苹果售价p元,总重m千克,箱重n千克,
则每千克苹果的售价是____________元.
分式的概念:
用A、B表示两个整式,A÷B就可以
表示成 形式。如果B中含有字母,B≠0,
式子 就叫做分式。其中,A叫做分式的
分子,B叫做分式的分母。
分式的特征是: ①分子、分母 是 ;
②分母中含有 。
字母
都
整式
分式
有理式
整式
单项式
多项式
分类:
例1:下列式子中哪些是整式,哪些是分式?
整式:(1),(4),(6),(7),(8)
分式:(2),(3),(5)
区分整式与分式的关键是看分母,分母中含有字母的是分式,不含字母的是整式。
练习1:
把下列各式的题号分别填入表中
(2)(3)(5)
(1)(4)(6)(7)
(1)(2)(3)(4)(5)(6)(7)
整 式 分 式 有 理 式
探索与发现(求代数式的值)
0
-1
0
0
-1
-1
-1
思考:
1、第2个分式在什么情况下无意义?
2、 这三个分式在什么情况下有意义?
3、这三个分式在什么情况下值为零?
无意义
无意义
x … -2 -1 0 1 2 …
… …
… …
… …
归纳:
对于分式
(1)分式无意义的条件是 。
(2)分式有意义的条件是 。
(3)分式的值为零的条件是 。
B=0
B≠0
A=0且B≠0
(分母为零)
(分母不为零)
(分子为零且分母不为零)
例2:当 取什么值时,下列分式有意义?
分 析
要使分式有意义,必须且只须分母不等于零。
解:
练习2
当 取何值时,下列分式有意义。
分 析
分式有意义的条件是分母不等于零。
例3:当 是什么数时,下列分式的值 为零?
3、当a取什么值时,分式 有意义。
练习3:
学以致用
求:当 1.分式的值为正时x的范围;
2.分式的值为负时x的范围.
谈一谈这一节课的收获和体会 。
①分子分母都是整式
②分母中必含有字母
分母中字母的取值不能使分母值为零,否则分式无意义
当分子为零且分母不为零时,分式值为零。
分式的概念
小测
1、(1)在下面四个有理式中,分式为( )(15分)
⑵
A、 B、 C、 D、- +
当x=-1时,下列分式没有意义的是( ) (15分)
A、 B、 C、 D、
2、⑴
⑵
