2019-2020学年人教版高中物理必修1课件第二章2.3《匀变速直线运动的位移与时间的关系》(共26张PPT)
文档属性
| 名称 | 2019-2020学年人教版高中物理必修1课件第二章2.3《匀变速直线运动的位移与时间的关系》(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-13 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
“适者生存”是自然界中基本的法则之一,猎豹要生存就必学获得足够的食物,猎豹的食物来源中,羚羊是不可缺少的,假设羚羊从静止开始奔跑,经50米能加速到最大速度25米每秒,并能维持较长的时间;猎豹从静止开始奔跑,经60米能加速到最大的速度30米每秒,以后只能维持这个速度4.0秒,设猎豹在某次寻找食物时,距离羚羊30米时开始攻击,羚羊在猎豹开始攻击后1.0秒才开始逃跑,
假定羚羊和猎豹在加速阶段分别做匀加速直线运动,且均沿着同一直线奔跑,猎豹能否成功捕获羚羊?
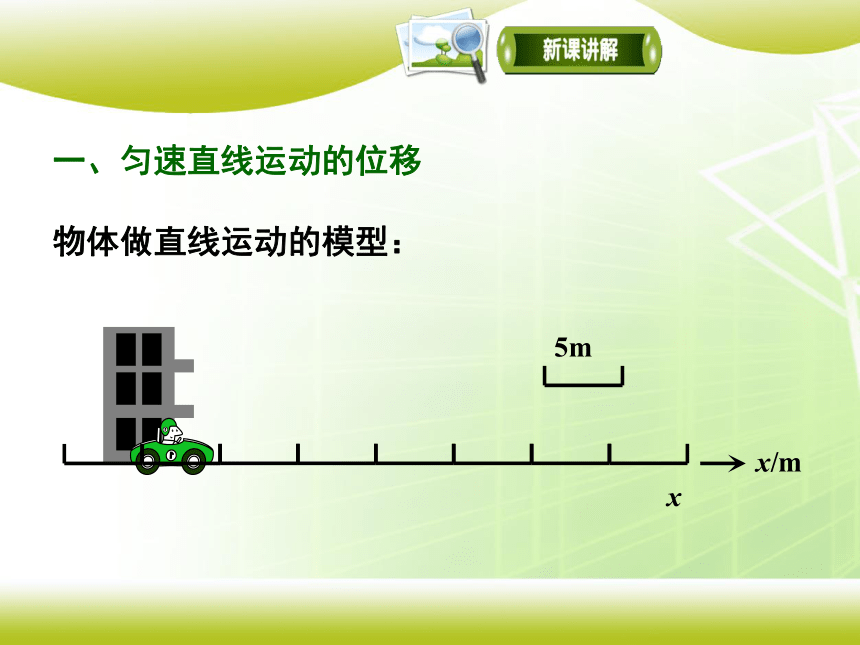
一、匀速直线运动的位移
物体做直线运动的模型:
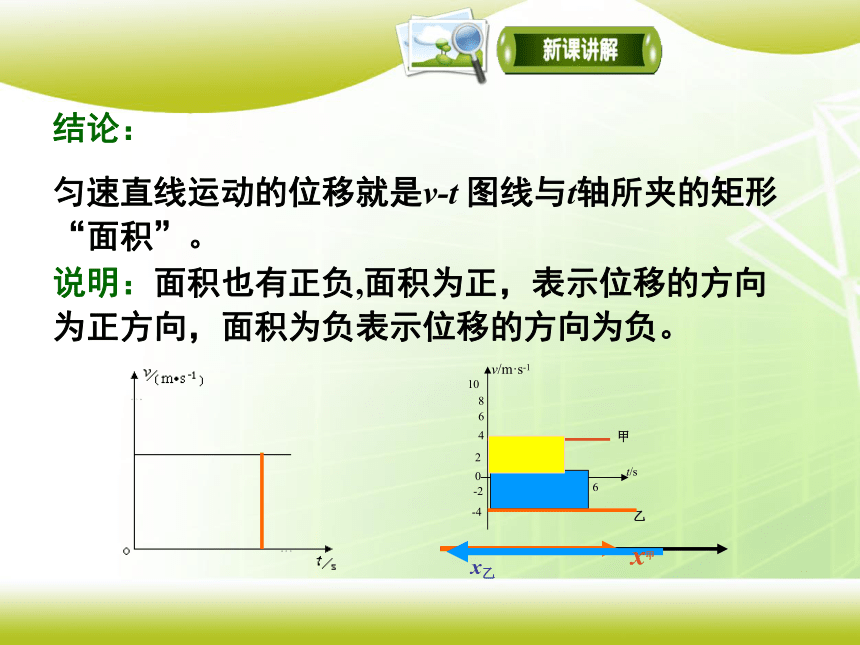
结论:
匀速直线运动的位移就是v-t 图线与t轴所夹的矩形“面积”。
说明:面积也有正负,面积为正,表示位移的方向为正方向,面积为负表示位移的方向为负。
二、匀变速直线运动的位移
阅读书中的材料,并讨论它的计算方法是否可行?
结论
学生A的计算中,时间间隔越小,计算出的误差就越小,越接近真实值。
说明
这种方法体现的科学思想是:先把过程无限分割,以“不变”近似代替“变”,然后再进行累加的思想 。
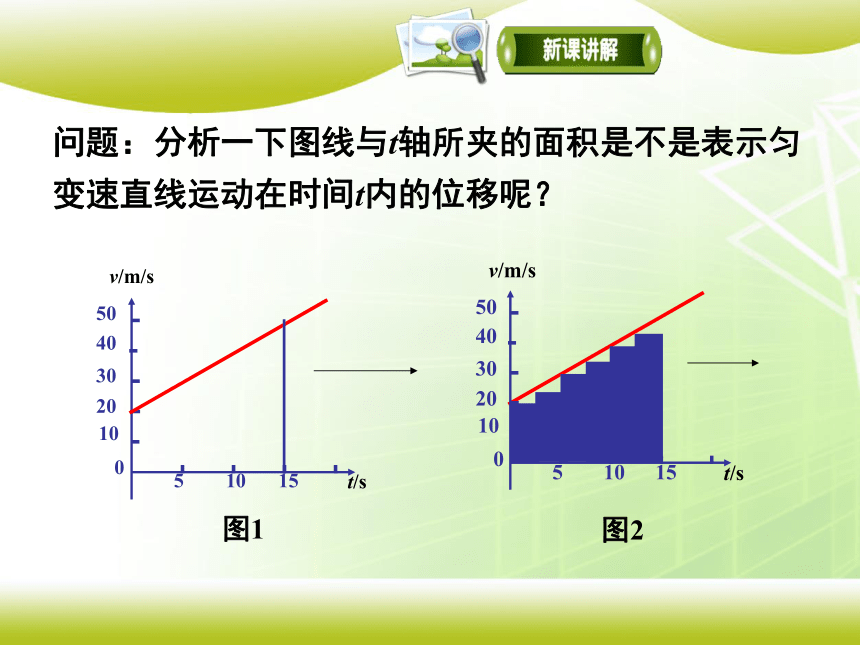
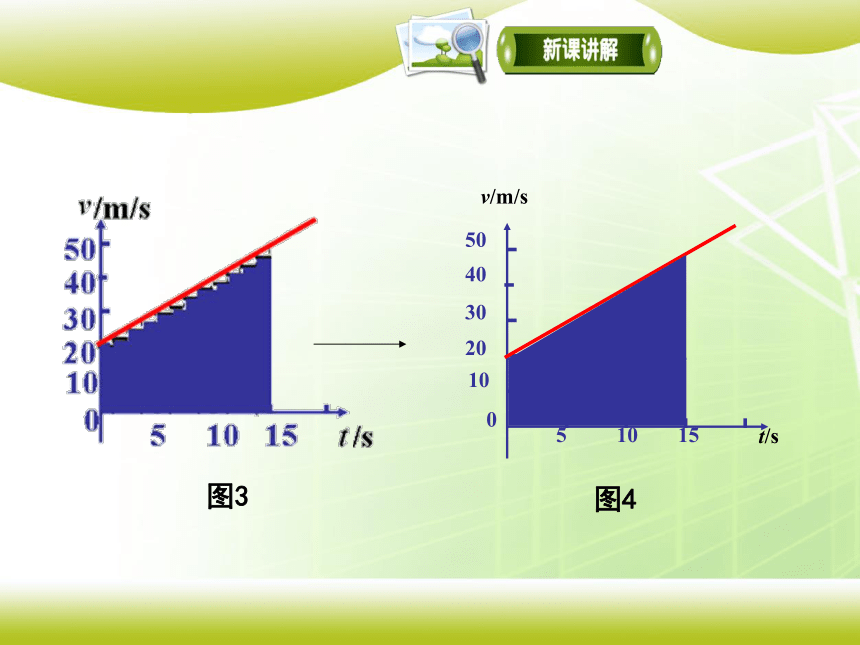
问题:分析一下图线与t轴所夹的面积是不是表示匀变速直线运动在时间t内的位移呢?
结论:梯形的面积就代表做匀变速直线运动物体在0(此时速度为v0)到 t(此时速度为v)这段时间的位移。
例题:飞机着陆后做匀变速直线运动,速度逐渐减小,已知
飞机着陆时的速度为60m/s,若前5s内通过的位移为225m,则
飞机的加速度大小为多少?此后飞机还要滑行多少秒才能停
止运动?
1.一辆汽车做匀减直线运动,初速度为15m/s,加速度大小为3m/s2,求:
(1)3s末速度的大小?
(2)物体的速度减为零所经历的时间?
(3)2s内的位移?
(4)第2s内的位移?
(5)8s内的汽车位移?
2.证明:物体做匀变速直线运动,在任意两个连续相等的时间内的位移之差等于一个常数。
3.已知一物体做匀变速直线运动,加速度为a,试证明在任意一段时间 t 内的平均速度等于该段时间中点时刻的瞬时速度。
我们可以躲开子弹
我们经常会在电影中看到这样的场景:为了躲避子弹,主人公纵身跳入河中。那么,他究竟需要潜多深才能躲过子弹呢?
任何物体在穿过某种介质(如水或空气)时都会受到阻力,从而使其速度减慢。介质的密度越大,所受的阻力也就越大,而水的密度是空气的700倍,因此子弹在水中的速度要比在空气中慢得多。
科学家通过一系列复杂的数学公式推算出:一颗速度为每秒300米的子弹在水中穿过几米后便会减慢,所以如果你想要躲避一颗子弹,在水中潜入3米深就足够了。
“适者生存”是自然界中基本的法则之一,猎豹要生存就必学获得足够的食物,猎豹的食物来源中,羚羊是不可缺少的,假设羚羊从静止开始奔跑,经50米能加速到最大速度25米每秒,并能维持较长的时间;猎豹从静止开始奔跑,经60米能加速到最大的速度30米每秒,以后只能维持这个速度4.0秒,设猎豹在某次寻找食物时,距离羚羊30米时开始攻击,羚羊在猎豹开始攻击后1.0秒才开始逃跑,
假定羚羊和猎豹在加速阶段分别做匀加速直线运动,且均沿着同一直线奔跑,猎豹能否成功捕获羚羊?
一、匀速直线运动的位移
物体做直线运动的模型:
结论:
匀速直线运动的位移就是v-t 图线与t轴所夹的矩形“面积”。
说明:面积也有正负,面积为正,表示位移的方向为正方向,面积为负表示位移的方向为负。
二、匀变速直线运动的位移
阅读书中的材料,并讨论它的计算方法是否可行?
结论
学生A的计算中,时间间隔越小,计算出的误差就越小,越接近真实值。
说明
这种方法体现的科学思想是:先把过程无限分割,以“不变”近似代替“变”,然后再进行累加的思想 。
问题:分析一下图线与t轴所夹的面积是不是表示匀变速直线运动在时间t内的位移呢?
结论:梯形的面积就代表做匀变速直线运动物体在0(此时速度为v0)到 t(此时速度为v)这段时间的位移。
例题:飞机着陆后做匀变速直线运动,速度逐渐减小,已知
飞机着陆时的速度为60m/s,若前5s内通过的位移为225m,则
飞机的加速度大小为多少?此后飞机还要滑行多少秒才能停
止运动?
1.一辆汽车做匀减直线运动,初速度为15m/s,加速度大小为3m/s2,求:
(1)3s末速度的大小?
(2)物体的速度减为零所经历的时间?
(3)2s内的位移?
(4)第2s内的位移?
(5)8s内的汽车位移?
2.证明:物体做匀变速直线运动,在任意两个连续相等的时间内的位移之差等于一个常数。
3.已知一物体做匀变速直线运动,加速度为a,试证明在任意一段时间 t 内的平均速度等于该段时间中点时刻的瞬时速度。
我们可以躲开子弹
我们经常会在电影中看到这样的场景:为了躲避子弹,主人公纵身跳入河中。那么,他究竟需要潜多深才能躲过子弹呢?
任何物体在穿过某种介质(如水或空气)时都会受到阻力,从而使其速度减慢。介质的密度越大,所受的阻力也就越大,而水的密度是空气的700倍,因此子弹在水中的速度要比在空气中慢得多。
科学家通过一系列复杂的数学公式推算出:一颗速度为每秒300米的子弹在水中穿过几米后便会减慢,所以如果你想要躲避一颗子弹,在水中潜入3米深就足够了。
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
