北师大版九年级数学上册6.2反比例函数的图像和性质课件(共41张ppt)
文档属性
| 名称 | 北师大版九年级数学上册6.2反比例函数的图像和性质课件(共41张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 731.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 00:00:00 | ||
图片预览









文档简介
课件41张PPT。数无形时少直觉,形少数时难入微。
数形结合百般好,隔离分家万事非。
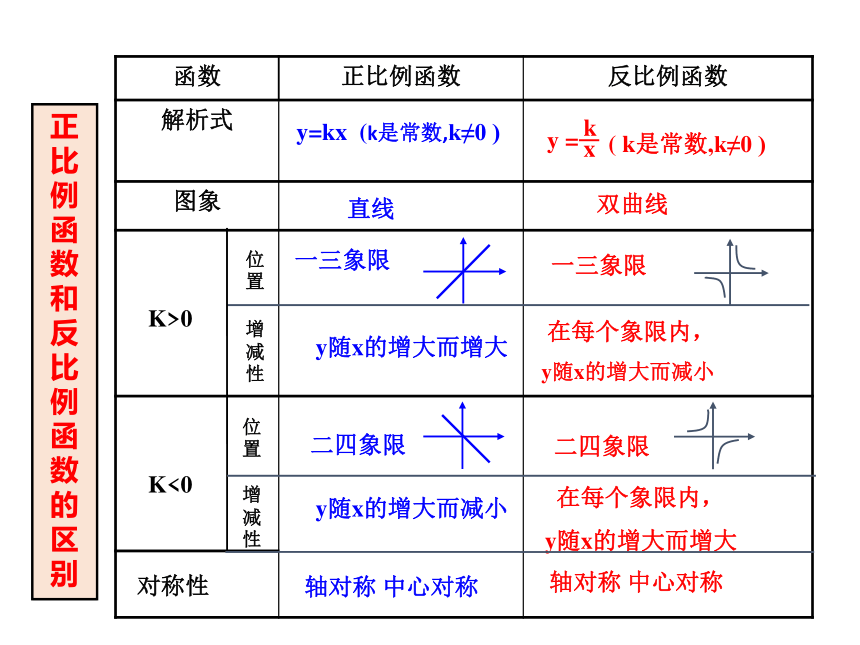
---------华罗庚6.2反比例函数的图像和性质二四象限一三象限位置增减性位置增减性y=kx (k是常数,k≠0 ) 直线 双曲线 y随x的增大而增大一三象限 在每个象限内,
y随x的增大而减小二四象限 y随x的增大而减小 在每个象限内,
y随x的增大而增大正比例函数和反比例函数的区别对称性 轴对称 中心对称 轴对称 中心对称专题一反比例函数的图像和性质解得:k=12∴这个反比例函数的表达式为∵k>0∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。∵图象过点A(2,6)题目一题目四题目二题目五题目三题目六反比例函数的图像和性质:
1.对于反比例函数y= (k为常数,k≠0),k的符号、图象所
经过的象限、函数的增减性这三者,知其一则知其二,即
k>0 图象在第一、三象限 在每个象限内y随x的增大而减小;
k<0 图象在第二、四象限 在每个象限内y随x的增大而增大.
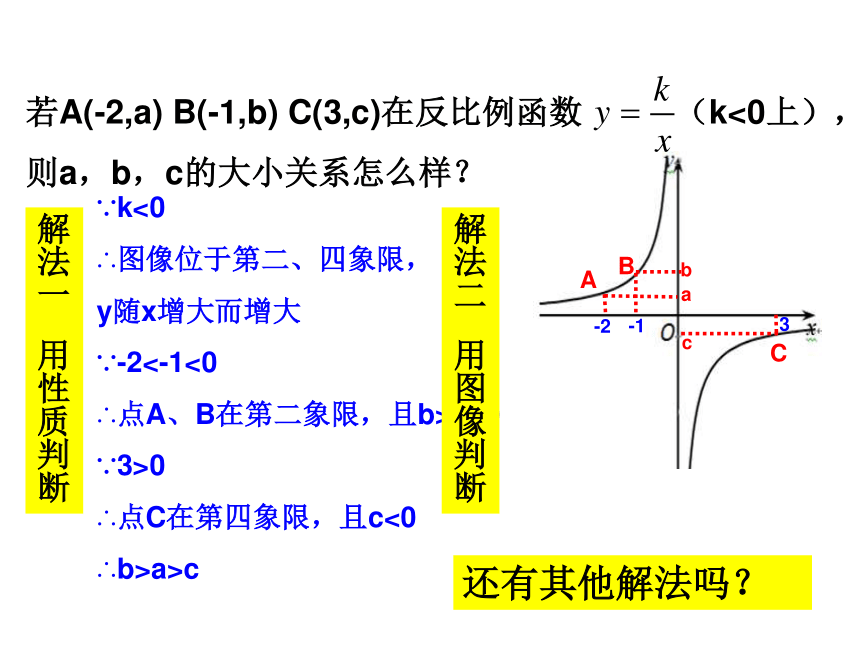
2.反比例函数的图象关于原点成中心对称.专题二简单应用:比较大小若A(-2,a) B(-1,b) C(3,c)在反比例函数 (k<0上),则a,b,c的大小关系怎么样?∵k<0
∴图像位于第二、四象限,
y随x增大而增大
∵-2<-1<0
∴点A、B在第二象限,且b>a>0
∵3>0
∴点C在第四象限,且c<0
∴b>a>c解法一 用性质判断解法二 用图像判断还有其他解法吗?ABCabc-1-23y1 >0>y22.若点A(-2,y1),B(-1,y2),C(2,y3)在
反比例函数 的图象上,则( )A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1C 关于反比例函数的增减性必须强调在每个分支上比较;反比例函数图象的位置和函数的增减性都由k的符号决定.专题三 K的几何意义反比例函数 图像上任取一点,过这一个点向x轴或y轴分别作垂线,这一点和垂足及坐标原点所构成的三角形的面积 ,并保持不变。 反比例函数 图像上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积均是 。 反比例函数y= 中k的几何意义如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是 .MNp例题3A A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3 S1S3S21.2.如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为_______.2E反比例函数y= (k为常数,k≠0)的几何意义的应用
1.由表达式求面积
2.由面积求表达式,需要考虑k的符号专题四与一次函数的结合已知函数y= 的图象如下右图,则y=k x-2 的图象大致是( )xxyyyyo(A)(B)Do2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中的图象大致是 ( )Cxxxyyy00 反比例函数图像只看象限,而一次函数既要看象限还要看与y轴的交点颗粒归仓通过这节课的学习,你有哪些收获?题目一题目四题目二题目五题目三题目六1.(2015·青岛中考)反比例函数y=- 的图象在( )
(A) 第一、二象限 (B) 第二、三象限
(C) 第一、三象限 (D) 第二、四象限2.(2016·潍坊中考)双曲线
在第一象限内的图象如图所示,作一条平
行于y轴的直线分别交双曲线于A、B两点,
连接OA、OB,则△AOB的面积为( )
(A)1 (B)2
(C)3 (D)4
A D 双曲线:
在第一象限内的图象如图所示,作一条平行于y轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )
(A)1 (B)2 (C)3 (D)4
拓展提高A C 如图,反比例函数 与一次函数 的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)求△AOB的面积.
家庭作业1.完成学案上的题目
2.电子书包的预习作业1.如果函数 为反比例函数,则m的值是 ( )
(A) -1 (B) 0 (C) (D) 1 返回B 2.如图,A为反比例函数 图象上一点,AB⊥ 轴于点B,若 则k为( )
(A) 6 (B) 3 (C) D 无法确定 返回A 3.函数 的图象经过(1,-1),则函数 的图象是 ( )
返回A 4.在同一坐标系中,函数 和 的图像大致是 ( )(D) (B) (C) (A) 返回C 5.已知反比例函数 的图像上有两点A( , ),B( , ),且 ,则 的值是( )(A)正数 (B)负数 (C)非正数(D) 不能确定返回D 6.如图:A,B是函数 的图象上关于原点O对称的任意两点。AC平行于y轴,BC平行于x轴,则△ABC的面积为( )
返回D (A)1 (B)4 (C) (D) 2-2返回A返回B返回SB返回5.关于反比例函数 y= 图象,下列说法正确的是( )
(A)必经过点(1,1) (B)两个分支分布在第二、四象限
(C)两个分支关于x轴成轴对称 (D)两个分支关于原点成中心对称D返回A返回A返回
数形结合百般好,隔离分家万事非。
---------华罗庚6.2反比例函数的图像和性质二四象限一三象限位置增减性位置增减性y=kx (k是常数,k≠0 ) 直线 双曲线 y随x的增大而增大一三象限 在每个象限内,
y随x的增大而减小二四象限 y随x的增大而减小 在每个象限内,
y随x的增大而增大正比例函数和反比例函数的区别对称性 轴对称 中心对称 轴对称 中心对称专题一反比例函数的图像和性质解得:k=12∴这个反比例函数的表达式为∵k>0∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。∵图象过点A(2,6)题目一题目四题目二题目五题目三题目六反比例函数的图像和性质:
1.对于反比例函数y= (k为常数,k≠0),k的符号、图象所
经过的象限、函数的增减性这三者,知其一则知其二,即
k>0 图象在第一、三象限 在每个象限内y随x的增大而减小;
k<0 图象在第二、四象限 在每个象限内y随x的增大而增大.
2.反比例函数的图象关于原点成中心对称.专题二简单应用:比较大小若A(-2,a) B(-1,b) C(3,c)在反比例函数 (k<0上),则a,b,c的大小关系怎么样?∵k<0
∴图像位于第二、四象限,
y随x增大而增大
∵-2<-1<0
∴点A、B在第二象限,且b>a>0
∵3>0
∴点C在第四象限,且c<0
∴b>a>c解法一 用性质判断解法二 用图像判断还有其他解法吗?ABCabc-1-23y1 >0>y22.若点A(-2,y1),B(-1,y2),C(2,y3)在
反比例函数 的图象上,则( )A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1C 关于反比例函数的增减性必须强调在每个分支上比较;反比例函数图象的位置和函数的增减性都由k的符号决定.专题三 K的几何意义反比例函数 图像上任取一点,过这一个点向x轴或y轴分别作垂线,这一点和垂足及坐标原点所构成的三角形的面积 ,并保持不变。 反比例函数 图像上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积均是 。 反比例函数y= 中k的几何意义如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是 .MNp例题3A A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3 S1S3S21.2.如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为_______.2E反比例函数y= (k为常数,k≠0)的几何意义的应用
1.由表达式求面积
2.由面积求表达式,需要考虑k的符号专题四与一次函数的结合已知函数y= 的图象如下右图,则y=k x-2 的图象大致是( )xxyyyyo(A)(B)Do2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中的图象大致是 ( )Cxxxyyy00 反比例函数图像只看象限,而一次函数既要看象限还要看与y轴的交点颗粒归仓通过这节课的学习,你有哪些收获?题目一题目四题目二题目五题目三题目六1.(2015·青岛中考)反比例函数y=- 的图象在( )
(A) 第一、二象限 (B) 第二、三象限
(C) 第一、三象限 (D) 第二、四象限2.(2016·潍坊中考)双曲线
在第一象限内的图象如图所示,作一条平
行于y轴的直线分别交双曲线于A、B两点,
连接OA、OB,则△AOB的面积为( )
(A)1 (B)2
(C)3 (D)4
A D 双曲线:
在第一象限内的图象如图所示,作一条平行于y轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )
(A)1 (B)2 (C)3 (D)4
拓展提高A C 如图,反比例函数 与一次函数 的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)求△AOB的面积.
家庭作业1.完成学案上的题目
2.电子书包的预习作业1.如果函数 为反比例函数,则m的值是 ( )
(A) -1 (B) 0 (C) (D) 1 返回B 2.如图,A为反比例函数 图象上一点,AB⊥ 轴于点B,若 则k为( )
(A) 6 (B) 3 (C) D 无法确定 返回A 3.函数 的图象经过(1,-1),则函数 的图象是 ( )
返回A 4.在同一坐标系中,函数 和 的图像大致是 ( )(D) (B) (C) (A) 返回C 5.已知反比例函数 的图像上有两点A( , ),B( , ),且 ,则 的值是( )(A)正数 (B)负数 (C)非正数(D) 不能确定返回D 6.如图:A,B是函数 的图象上关于原点O对称的任意两点。AC平行于y轴,BC平行于x轴,则△ABC的面积为( )
返回D (A)1 (B)4 (C) (D) 2-2返回A返回B返回SB返回5.关于反比例函数 y= 图象,下列说法正确的是( )
(A)必经过点(1,1) (B)两个分支分布在第二、四象限
(C)两个分支关于x轴成轴对称 (D)两个分支关于原点成中心对称D返回A返回A返回
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
