人教新课标A版选修2-1第一章 常用逻辑用语1.1.2 四种命题1.1.3 四种命题间的相互关系(25张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第一章 常用逻辑用语1.1.2 四种命题1.1.3 四种命题间的相互关系(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 912.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 15:33:25 | ||
图片预览







文档简介
课件25张PPT。1.1.2 四种命题
1.1.3 四种命题间的相互关系新知探求 素养养成知识点一 四种命题的概念问题1:初中已学过命题与逆命题的知识,什么叫做命题的逆命题?
答案:在两个命题中,如果第一个命题的条件是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫做互为逆命题.
问题2:除命题与逆命题之外是否还有其他形式的命题?
答案:有.
梳理 (1)互逆命题:一般地,对于两个命题,一个命题的条件和结论分别是另一个命题的 ,这样的两个命题叫做互逆命题,把其中一个命题叫做原命题,另一个命题叫做原命题的 .结论和条件 逆命题(2)互否命题:一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定,这样的两个命题叫做互否命题,把其中的一个命题叫做原命题,另一个命题叫做原命题的 .
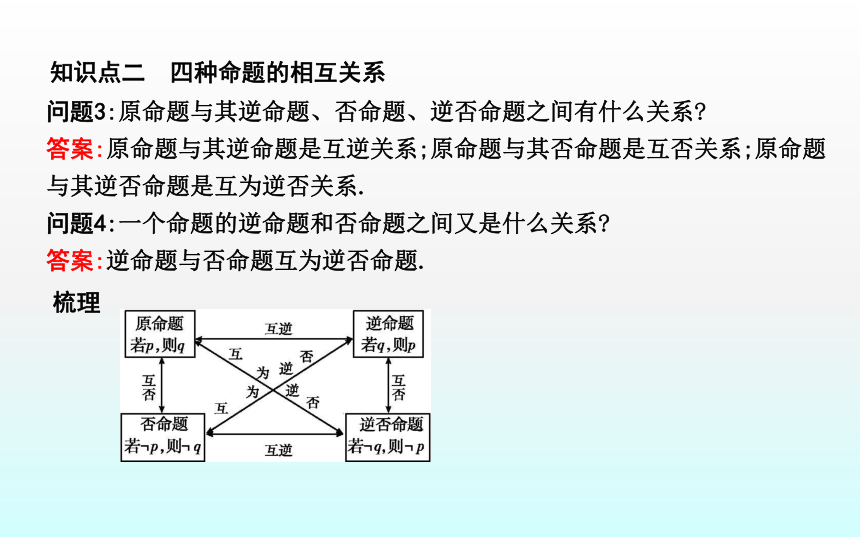
(3)互为逆否命题:一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定,这样的两个命题叫做互为逆否命题,把其中的一个命题叫做原命题,另一个命题叫做原命题的 .否命题逆否命题知识点二 四种命题的相互关系问题3:原命题与其逆命题、否命题、逆否命题之间有什么关系?
答案:原命题与其逆命题是互逆关系;原命题与其否命题是互否关系;原命题与其逆否命题是互为逆否关系.
问题4:一个命题的逆命题和否命题之间又是什么关系?
答案:逆命题与否命题互为逆否命题.梳理 知识点三 四种命题的真假问题5:写出命题“若α=30°,则sin α= ”的逆命题、否命题、逆否命题,并判断真假.问题6:上述四种命题的真假性之间有关系吗?若有,有何关系?
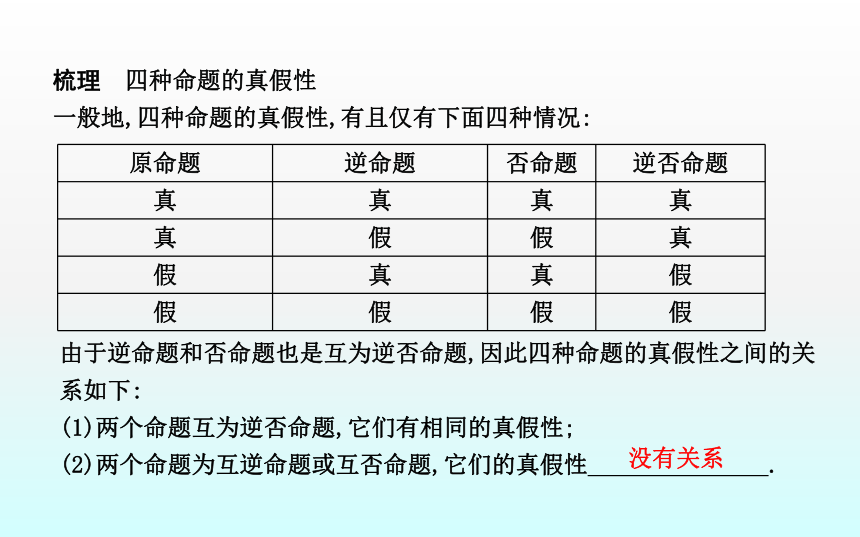
答案:原命题与逆否命题的真假性相同;逆命题与否命题的真假性相同,原命题与逆命题、否命题的真假没关系.梳理 四种命题的真假性
一般地,四种命题的真假性,有且仅有下面四种情况:由于逆命题和否命题也是互为逆否命题,因此四种命题的真假性之间的关系如下:
(1)两个命题互为逆否命题,它们有相同的真假性;
(2)两个命题为互逆命题或互否命题,它们的真假性 .没有关系名师点津:四种命题的两个关注点
(1)写原命题的逆命题时,不要交换命题的前提条件.
(2)写一个命题的否命题时,要对命题的条件和结论都进行否定,避免出现不否定条件,而只否定结论的错误.题型一 四种命题的概念课堂探究 素养提升【例1】 写出下列命题的逆命题、否命题和逆否命题.
(1)垂直于同一平面的两直线平行.
(2)若m·n<0,则方程mx2-x+n=0有实数根.解:(1)逆命题:如果两条直线平行,那么这两条直线垂直于同一个平面.
否命题:如果两条直线不垂直于同一平面,那么这两条直线不平行.
逆否命题:如果两条直线不平行,那么这两条直线不垂直于同一平面.
(2)逆命题:若方程mx2-x+n=0有实数根,则m·n<0.
否命题:若m·n≥0,则方程mx2-x+n=0没有实数根.
逆否命题:若方程mx2-x+n=0没有实数根,则m·n≥0.方法技巧 写出一个命题的其他三种命题的步骤
(1)分析命题的条件和结论;
(2)将命题写成“若p,则q”的形式;(3)根据逆命题、否命题、逆否命题各自的结构形式写出这三种命题.即时训练1-1:(1)命题“若一个数是负数,则它的平方是正数”的逆命题是( )
(A)“若一个数是负数,则它的平方不是正数”
(B)“若一个数的平方是正数,则它是负数”
(C)“若一个数不是负数,则它的平方不是正数”
(D)“若一个数的平方不是正数,则它不是负数”解析:(1)因为一个命题的逆命题是将原命题的条件与结论进行交换,因此逆命题为“若一个数的平方是正数,则它是负数”.故选B.(2)(2018·武汉二中期末)已知a,b,c∈R,命题“若a+b+c=3,则a2+b2+c2≥3”的否命题是( )
(A)若a+b+c≠3,则a2+b2+c2<3
(B)若a+b+c=3,则a2+b2+c2<3
(C)若a+b+c≠3,则a2+b2+c2≥3
(D)若a2+b2+c2≥3,则a+b+c=3解析:(2)根据四种命题的定义,
命题“若a+b+c=3,则a2+b2+c2≥3”的否命题是
“若a+b+c≠3,则a2+b2+c2<3”.
故选A.(3)(2018·北京西城期末)设m∈R,命题“若m≥0,则方程x2=m有实根”的逆否命题是( )
(A)若方程x2=m有实根,则m≥0
(B)若方程x2=m有实根,则m<0
(C)若方程x2=m没有实根,则m≥0
(D)若方程x2=m没有实根,则m<0解析:(3)命题“若m≥0,则方程x2=m有实根”的逆否命题是命题“若方程x2=m没有实根,则m<0”.故选D.【备用例1】 (1)(2018·广西桂林期末)命题“若整数a,b都是偶数,则a+b是偶数”的逆否命题为( )
(A)若整数a,b中有一个偶数,则a+b是偶数
(B)若整数a,b都不是偶数,则a+b不是偶数
(C)若a+b不是偶数,则整数a,b都不是偶数
(D)若a+b不是偶数,则整数a,b不都是偶数解析:(1)命题“若整数a,b都是偶数,则a+b是偶数”的逆否命题为“若a+b不是偶数,则整数a,b不都是偶数”.故选D.答案:(1)D (2)下列说法错误的是 .?
①“四条边相等的四边形是正方形”的否命题是“四条边相等的四边形不是正方形”;
②“若x2=9,则x=3”的否命题的逆否命题是“若x2≠9,则x≠3”;
③“若a>b,则7a>7b”的逆否命题是“若7a≤7b,则a≤b”.解析:(2)①“四条边相等的四边形是正方形”的否命题是“四条边不相等的四边形不是正方形”,故①错;
②“若x2=9,则x=3”的否命题为“若x2≠9,则x≠3”,“若x2≠9,则x≠3”的逆否命题为“若x=3,则x2=9”,故②错.
③正确.答案:(2)①②题型二 四种命题的关系及真假判断【例2】 判断下列命题的真假.
(1)“若x2+y2≠0,则x,y不全为零”的否命题;
(2)“正三角形都相似”的逆命题;
(3)“若m>0,则x2+x-m=0有实根”的逆否命题.解析:(1)原命题的否命题为“若x2+y2=0,则x,y全为零”.真命题.
(2)原命题的逆命题为“若三角形相似,则这些三角形是正三角形”.假命题.(3)原命题的逆否命题为“若x2+x-m=0无实根,则m≤0”.
若方程x2+x-m=0无实根,
则判别式Δ=1+4m<0,
解得m<- ,
故m≤0,为真命题.一题多变:(1)若本例(3)改为判断“若m>0,则x2+x-m=0有实根”的逆命题的真假,则结果如何?
(2)若本例(3)改为判断“若m>0,则mx2+x-1=0有实根”的逆否命题的真假,则结论如何?解:(1)原命题的逆命题为“若x2+x-m=0有实根,则m>0”.
若方程x2+x-m=0有实根,
则判别式Δ=1+4m≥0,所以m≥- ,
故逆命题为假命题.(2)原命题的逆否命题为“若mx2+x-1=0无实根,则m≤0”.
若方程mx2+x-1=0无实根,则m≠0,
判别式Δ=1+4m<0,
则m<- ,故m≤0,为真命题.方法技巧 (1)由原命题写出其他三种命题,依次直接判断这四种命题的真假.(2)也可根据命题间的等价关系来判断命题的真假,注意:(3)四种命题中,真命题的个数只可能为0个,2个,4个.(A)0 (B)1 (C)2 (D)4(2)(2018·福建漳州程溪中学期中)下列四个命题中:
①“等边三角形的三个内角均为60°”的逆命题;
②“若k>0,则方程x2+2x-k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题;
④“若ab≠0,则a≠0”的否命题.
其中真命题的序号是( )
(A)②③ (B)③④ (C)①④ (D)①②解析:(2)对于①“等边三角形的三个内角均为60°”的逆命题:三个内角均为60°的三角形是等边三角形,为真命题;
对于②,“若k>0,则方程x2+2x-k=0的Δ=4+4k>0,有实根”,所以原命题为真,其逆否命题与原命题同真假,为真命题;
对于③,“全等三角形的面积相等”的否命题:不全等三角形的面积不相等,为假命题;
对于④,“若ab≠0,则a≠0”的否命题:“若ab=0,则a=0”,为假命题.
故选D.题型三 等价命题的应用【例3】 (12分)已知函数f(x)在(-∞,+∞)上是增函数,a,b∈R,对命题“若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b).”
写出其逆命题,判断其真假,并证明你的结论.规范解答:逆命题:若f(a)+f(b)≥f(-a)+f(-b),则a+b≥0.为真命题.…………2分
由于逆命题与否命题具有相同的真假性,因此可转化为证明其否命题为真,即证明“若a+b<0,则f(a)+f(b)因为a+b<0,则a<-b,b<-a.
因为f(x)在(-∞,+∞)上为增函数,
则f(a)所以f(a)+f(b)因此否命题为真命题,即逆命题为真命题.………………………………………12分方法技巧 直接证明困难时,命题是否定的形式或不等式的形式时,常常考虑用证明逆否命题的方法来证明.即时训练3-1:证明:如果p2+q2=2,则p+q≤2.证明:该命题的逆否命题为若p+q>2,则p2+q2≠2.
因为原命题与其逆否命题的真假性相同,故只需证明其逆否命题为真命题即可.
因为p+q>2,所以(p+q)2>4.
因为p2+q2≥2pq,
所以p2+q2>2.
即p+q>2时,p2+q2≠2成立.
所以如果p2+q2=2,则p+q≤2成立.题型四 易错辨析——不能正确否定致误【例4】 命题:“a,b都是奇数,则a+b是偶数”的逆否命题是 ,是 (选填“真”或“假”)命题.?错解:若a+b不是偶数,则a,b都不是奇数,是假命题.
纠错:“都是”的否定应为“不都是”.本题因否定“都是”时出错,从而导致真假性判断错误.
正解:若a+b不是偶数,则a,b不都是奇数 真谢谢观赏!
1.1.3 四种命题间的相互关系新知探求 素养养成知识点一 四种命题的概念问题1:初中已学过命题与逆命题的知识,什么叫做命题的逆命题?
答案:在两个命题中,如果第一个命题的条件是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫做互为逆命题.
问题2:除命题与逆命题之外是否还有其他形式的命题?
答案:有.
梳理 (1)互逆命题:一般地,对于两个命题,一个命题的条件和结论分别是另一个命题的 ,这样的两个命题叫做互逆命题,把其中一个命题叫做原命题,另一个命题叫做原命题的 .结论和条件 逆命题(2)互否命题:一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定,这样的两个命题叫做互否命题,把其中的一个命题叫做原命题,另一个命题叫做原命题的 .
(3)互为逆否命题:一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定,这样的两个命题叫做互为逆否命题,把其中的一个命题叫做原命题,另一个命题叫做原命题的 .否命题逆否命题知识点二 四种命题的相互关系问题3:原命题与其逆命题、否命题、逆否命题之间有什么关系?
答案:原命题与其逆命题是互逆关系;原命题与其否命题是互否关系;原命题与其逆否命题是互为逆否关系.
问题4:一个命题的逆命题和否命题之间又是什么关系?
答案:逆命题与否命题互为逆否命题.梳理 知识点三 四种命题的真假问题5:写出命题“若α=30°,则sin α= ”的逆命题、否命题、逆否命题,并判断真假.问题6:上述四种命题的真假性之间有关系吗?若有,有何关系?
答案:原命题与逆否命题的真假性相同;逆命题与否命题的真假性相同,原命题与逆命题、否命题的真假没关系.梳理 四种命题的真假性
一般地,四种命题的真假性,有且仅有下面四种情况:由于逆命题和否命题也是互为逆否命题,因此四种命题的真假性之间的关系如下:
(1)两个命题互为逆否命题,它们有相同的真假性;
(2)两个命题为互逆命题或互否命题,它们的真假性 .没有关系名师点津:四种命题的两个关注点
(1)写原命题的逆命题时,不要交换命题的前提条件.
(2)写一个命题的否命题时,要对命题的条件和结论都进行否定,避免出现不否定条件,而只否定结论的错误.题型一 四种命题的概念课堂探究 素养提升【例1】 写出下列命题的逆命题、否命题和逆否命题.
(1)垂直于同一平面的两直线平行.
(2)若m·n<0,则方程mx2-x+n=0有实数根.解:(1)逆命题:如果两条直线平行,那么这两条直线垂直于同一个平面.
否命题:如果两条直线不垂直于同一平面,那么这两条直线不平行.
逆否命题:如果两条直线不平行,那么这两条直线不垂直于同一平面.
(2)逆命题:若方程mx2-x+n=0有实数根,则m·n<0.
否命题:若m·n≥0,则方程mx2-x+n=0没有实数根.
逆否命题:若方程mx2-x+n=0没有实数根,则m·n≥0.方法技巧 写出一个命题的其他三种命题的步骤
(1)分析命题的条件和结论;
(2)将命题写成“若p,则q”的形式;(3)根据逆命题、否命题、逆否命题各自的结构形式写出这三种命题.即时训练1-1:(1)命题“若一个数是负数,则它的平方是正数”的逆命题是( )
(A)“若一个数是负数,则它的平方不是正数”
(B)“若一个数的平方是正数,则它是负数”
(C)“若一个数不是负数,则它的平方不是正数”
(D)“若一个数的平方不是正数,则它不是负数”解析:(1)因为一个命题的逆命题是将原命题的条件与结论进行交换,因此逆命题为“若一个数的平方是正数,则它是负数”.故选B.(2)(2018·武汉二中期末)已知a,b,c∈R,命题“若a+b+c=3,则a2+b2+c2≥3”的否命题是( )
(A)若a+b+c≠3,则a2+b2+c2<3
(B)若a+b+c=3,则a2+b2+c2<3
(C)若a+b+c≠3,则a2+b2+c2≥3
(D)若a2+b2+c2≥3,则a+b+c=3解析:(2)根据四种命题的定义,
命题“若a+b+c=3,则a2+b2+c2≥3”的否命题是
“若a+b+c≠3,则a2+b2+c2<3”.
故选A.(3)(2018·北京西城期末)设m∈R,命题“若m≥0,则方程x2=m有实根”的逆否命题是( )
(A)若方程x2=m有实根,则m≥0
(B)若方程x2=m有实根,则m<0
(C)若方程x2=m没有实根,则m≥0
(D)若方程x2=m没有实根,则m<0解析:(3)命题“若m≥0,则方程x2=m有实根”的逆否命题是命题“若方程x2=m没有实根,则m<0”.故选D.【备用例1】 (1)(2018·广西桂林期末)命题“若整数a,b都是偶数,则a+b是偶数”的逆否命题为( )
(A)若整数a,b中有一个偶数,则a+b是偶数
(B)若整数a,b都不是偶数,则a+b不是偶数
(C)若a+b不是偶数,则整数a,b都不是偶数
(D)若a+b不是偶数,则整数a,b不都是偶数解析:(1)命题“若整数a,b都是偶数,则a+b是偶数”的逆否命题为“若a+b不是偶数,则整数a,b不都是偶数”.故选D.答案:(1)D (2)下列说法错误的是 .?
①“四条边相等的四边形是正方形”的否命题是“四条边相等的四边形不是正方形”;
②“若x2=9,则x=3”的否命题的逆否命题是“若x2≠9,则x≠3”;
③“若a>b,则7a>7b”的逆否命题是“若7a≤7b,则a≤b”.解析:(2)①“四条边相等的四边形是正方形”的否命题是“四条边不相等的四边形不是正方形”,故①错;
②“若x2=9,则x=3”的否命题为“若x2≠9,则x≠3”,“若x2≠9,则x≠3”的逆否命题为“若x=3,则x2=9”,故②错.
③正确.答案:(2)①②题型二 四种命题的关系及真假判断【例2】 判断下列命题的真假.
(1)“若x2+y2≠0,则x,y不全为零”的否命题;
(2)“正三角形都相似”的逆命题;
(3)“若m>0,则x2+x-m=0有实根”的逆否命题.解析:(1)原命题的否命题为“若x2+y2=0,则x,y全为零”.真命题.
(2)原命题的逆命题为“若三角形相似,则这些三角形是正三角形”.假命题.(3)原命题的逆否命题为“若x2+x-m=0无实根,则m≤0”.
若方程x2+x-m=0无实根,
则判别式Δ=1+4m<0,
解得m<- ,
故m≤0,为真命题.一题多变:(1)若本例(3)改为判断“若m>0,则x2+x-m=0有实根”的逆命题的真假,则结果如何?
(2)若本例(3)改为判断“若m>0,则mx2+x-1=0有实根”的逆否命题的真假,则结论如何?解:(1)原命题的逆命题为“若x2+x-m=0有实根,则m>0”.
若方程x2+x-m=0有实根,
则判别式Δ=1+4m≥0,所以m≥- ,
故逆命题为假命题.(2)原命题的逆否命题为“若mx2+x-1=0无实根,则m≤0”.
若方程mx2+x-1=0无实根,则m≠0,
判别式Δ=1+4m<0,
则m<- ,故m≤0,为真命题.方法技巧 (1)由原命题写出其他三种命题,依次直接判断这四种命题的真假.(2)也可根据命题间的等价关系来判断命题的真假,注意:(3)四种命题中,真命题的个数只可能为0个,2个,4个.(A)0 (B)1 (C)2 (D)4(2)(2018·福建漳州程溪中学期中)下列四个命题中:
①“等边三角形的三个内角均为60°”的逆命题;
②“若k>0,则方程x2+2x-k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题;
④“若ab≠0,则a≠0”的否命题.
其中真命题的序号是( )
(A)②③ (B)③④ (C)①④ (D)①②解析:(2)对于①“等边三角形的三个内角均为60°”的逆命题:三个内角均为60°的三角形是等边三角形,为真命题;
对于②,“若k>0,则方程x2+2x-k=0的Δ=4+4k>0,有实根”,所以原命题为真,其逆否命题与原命题同真假,为真命题;
对于③,“全等三角形的面积相等”的否命题:不全等三角形的面积不相等,为假命题;
对于④,“若ab≠0,则a≠0”的否命题:“若ab=0,则a=0”,为假命题.
故选D.题型三 等价命题的应用【例3】 (12分)已知函数f(x)在(-∞,+∞)上是增函数,a,b∈R,对命题“若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b).”
写出其逆命题,判断其真假,并证明你的结论.规范解答:逆命题:若f(a)+f(b)≥f(-a)+f(-b),则a+b≥0.为真命题.…………2分
由于逆命题与否命题具有相同的真假性,因此可转化为证明其否命题为真,即证明“若a+b<0,则f(a)+f(b)
因为f(x)在(-∞,+∞)上为增函数,
则f(a)
因为原命题与其逆否命题的真假性相同,故只需证明其逆否命题为真命题即可.
因为p+q>2,所以(p+q)2>4.
因为p2+q2≥2pq,
所以p2+q2>2.
即p+q>2时,p2+q2≠2成立.
所以如果p2+q2=2,则p+q≤2成立.题型四 易错辨析——不能正确否定致误【例4】 命题:“a,b都是奇数,则a+b是偶数”的逆否命题是 ,是 (选填“真”或“假”)命题.?错解:若a+b不是偶数,则a,b都不是奇数,是假命题.
纠错:“都是”的否定应为“不都是”.本题因否定“都是”时出错,从而导致真假性判断错误.
正解:若a+b不是偶数,则a,b不都是奇数 真谢谢观赏!
