人教新课标A版选修2-1第二章 圆锥曲线与方程2.2.2第1课时 椭圆的简单几何性质(27张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第二章 圆锥曲线与方程2.2.2第1课时 椭圆的简单几何性质(27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 15:44:21 | ||
图片预览






文档简介
课件27张PPT。2.2.2 椭圆的简单几何性质
第一课时 椭圆的简单几何性质新知探求 素养养成知识点 椭圆的简单几何性质1.通过观察图象,你发现椭圆C1、椭圆C2上的点的坐标的范围是怎样的?答案:椭圆C1上的点:-5≤x≤5,-4≤y≤4.椭圆C2上的点:-4≤x≤4,-5≤y≤5.答案:椭圆关于y轴对称,椭圆还关于x轴、原点对称.
3.两个椭圆的形状相同吗?为什么?
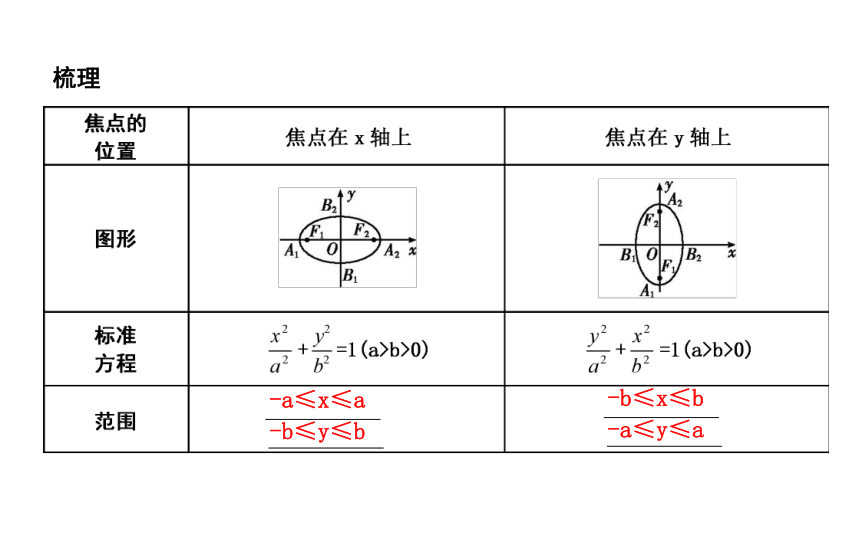
答案:两个椭圆的形状相同只是位置不同.因为两个椭圆的长、短轴的长度分别相等.梳理 -a≤x≤a
-b≤y≤b -b≤x≤b
-a≤y≤aA1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)A1(0,-a),A2(0,a)
B1(-b,0),B2(b,0)2b2aF1(-c,0),F2(c,0)F1(0,-c),F2(0,c)2cx轴,y轴 (0,0) 名师点津:(1)椭圆的范围
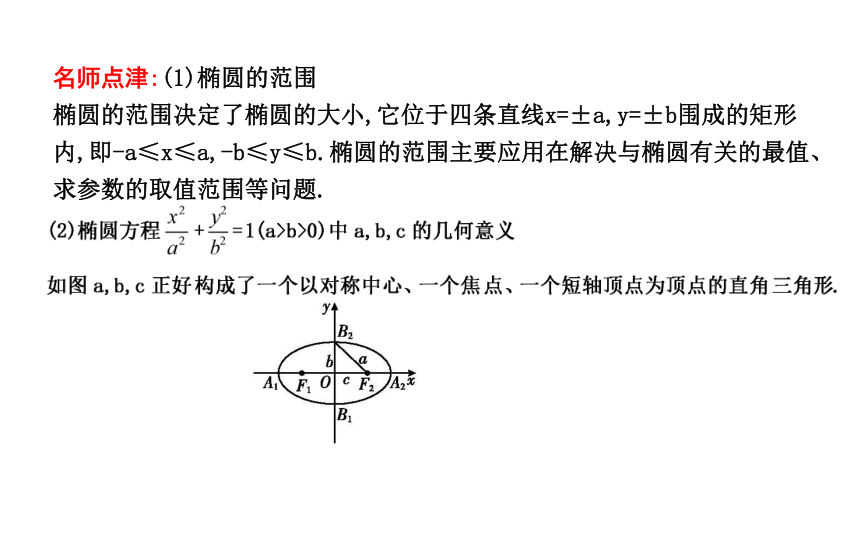
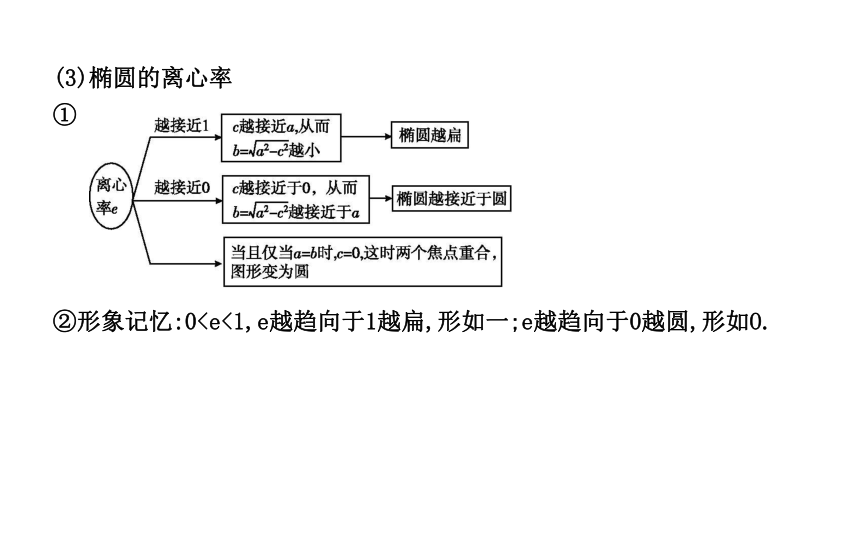
椭圆的范围决定了椭圆的大小,它位于四条直线x=±a,y=±b围成的矩形内,即-a≤x≤a,-b≤y≤b.椭圆的范围主要应用在解决与椭圆有关的最值、求参数的取值范围等问题.(3)椭圆的离心率
①②形象记忆:0(2)焦点位置不确定的要分类讨论,找准a与b,正确利用a2=b2+c2求出焦点坐标,再写出顶点坐标.同时要注意长轴长、短轴长、焦距不是a,b,c,而应是a,b,c的两倍.②当椭圆的焦点在y轴上时,有m<2,有2-m=1,解可得m=1.
综上可得,m=3或m=1,
故选B.①求椭圆C1的长半轴长、短半轴长、焦点坐标及离心率;
②写出椭圆C2的方程,并研究其性质.题型二 由椭圆的几何性质求椭圆方程【例2】 求适合下列条件的椭圆的标准方程.
(1)长轴长是短轴长的5倍,且过点A(5,0);方法技巧 利用待定系数法求椭圆标准方程的基本步骤及注意事项
(1)基本步骤(2)注意事项:当椭圆的焦点位置不确定时,通常要分类讨论,分别设出标准方程求解,可确定类型的量有焦点、顶点;而不能确定类型的量有长轴长、短轴长、离心率、焦距.题型三 椭圆的离心率【例3】 (2018·湖州市菱湖中学高二期中)已知F1,F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是正三角形,则这个椭圆的离心率是 .?一题多变1:本例中,若将条件“若△ABF2是正三角形”改为“若△ABF2是直角三角形”,试求椭圆的离心率.一题多变2:本例中,若将条件“若△ABF2是正三角形”改为“若△ABF2是锐角三角形”,试求椭圆离心率的取值范围.方法技巧 求椭圆的离心率的思路
一是先求a,c,再计算e;二是依据条件的信息,结合有关知识和a,b,c,e的关系,构造关于e的方程,再求解,求解时应注意离心率e的范围是(0,1).谢谢观赏!
第一课时 椭圆的简单几何性质新知探求 素养养成知识点 椭圆的简单几何性质1.通过观察图象,你发现椭圆C1、椭圆C2上的点的坐标的范围是怎样的?答案:椭圆C1上的点:-5≤x≤5,-4≤y≤4.椭圆C2上的点:-4≤x≤4,-5≤y≤5.答案:椭圆关于y轴对称,椭圆还关于x轴、原点对称.
3.两个椭圆的形状相同吗?为什么?
答案:两个椭圆的形状相同只是位置不同.因为两个椭圆的长、短轴的长度分别相等.梳理 -a≤x≤a
-b≤y≤b -b≤x≤b
-a≤y≤aA1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)A1(0,-a),A2(0,a)
B1(-b,0),B2(b,0)2b2aF1(-c,0),F2(c,0)F1(0,-c),F2(0,c)2cx轴,y轴 (0,0) 名师点津:(1)椭圆的范围
椭圆的范围决定了椭圆的大小,它位于四条直线x=±a,y=±b围成的矩形内,即-a≤x≤a,-b≤y≤b.椭圆的范围主要应用在解决与椭圆有关的最值、求参数的取值范围等问题.(3)椭圆的离心率
①②形象记忆:0
综上可得,m=3或m=1,
故选B.①求椭圆C1的长半轴长、短半轴长、焦点坐标及离心率;
②写出椭圆C2的方程,并研究其性质.题型二 由椭圆的几何性质求椭圆方程【例2】 求适合下列条件的椭圆的标准方程.
(1)长轴长是短轴长的5倍,且过点A(5,0);方法技巧 利用待定系数法求椭圆标准方程的基本步骤及注意事项
(1)基本步骤(2)注意事项:当椭圆的焦点位置不确定时,通常要分类讨论,分别设出标准方程求解,可确定类型的量有焦点、顶点;而不能确定类型的量有长轴长、短轴长、离心率、焦距.题型三 椭圆的离心率【例3】 (2018·湖州市菱湖中学高二期中)已知F1,F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是正三角形,则这个椭圆的离心率是 .?一题多变1:本例中,若将条件“若△ABF2是正三角形”改为“若△ABF2是直角三角形”,试求椭圆的离心率.一题多变2:本例中,若将条件“若△ABF2是正三角形”改为“若△ABF2是锐角三角形”,试求椭圆离心率的取值范围.方法技巧 求椭圆的离心率的思路
一是先求a,c,再计算e;二是依据条件的信息,结合有关知识和a,b,c,e的关系,构造关于e的方程,再求解,求解时应注意离心率e的范围是(0,1).谢谢观赏!
