人教新课标A版选修2-1第二章 圆锥曲线与方程2.4.1 抛物线及其标准方程(24张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第二章 圆锥曲线与方程2.4.1 抛物线及其标准方程(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 15:55:17 | ||
图片预览







文档简介
课件24张PPT。2.4 抛物线
2.4.1 抛物线及其标准方程新知探求 素养养成知识点一梳理 抛物线的定义
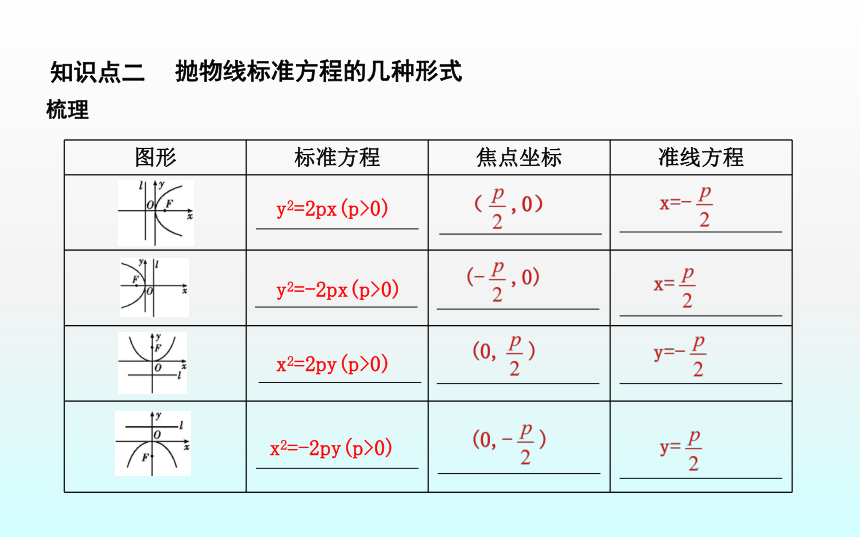
平面内与一个定点F和一条定直线l(l不经过点F)距离 的点的轨迹叫做抛物线,点F叫做抛物线的 ,直线l叫做抛物线的 .相等焦点准线抛物线的定义知识点二梳理 抛物线标准方程的几种形式y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)题型一 抛物线定义的应用课堂探究 素养提升(2)是否存在M,使|MA|+|MF|取得最小值?若存在,求此时点M的坐标;若不存在,请说明理由.规范解答:(2)如图,由于点M在抛物线上,
所以|MF|等于点M到其准线l的距离|MN|,于是|MA|+|MF|=|MA|+|MN|,
…………………………………………………………………8分
所以当A,M,N三点共线时,|MA|+|MN|取最小值,亦即|MA|+|MF|取最小值,这时M的纵坐标为2,…………………………………………10分
分可设M(x0,2),代入抛物线方程得x0=2,即M(2,2).…………
………………………………………………………………12分方法技巧 (1)抛物线的定义中指明了抛物线上的点到焦点的距离与到准线的距离相等,故两者可相互转化,这也是利用抛物线定义解题的实质.
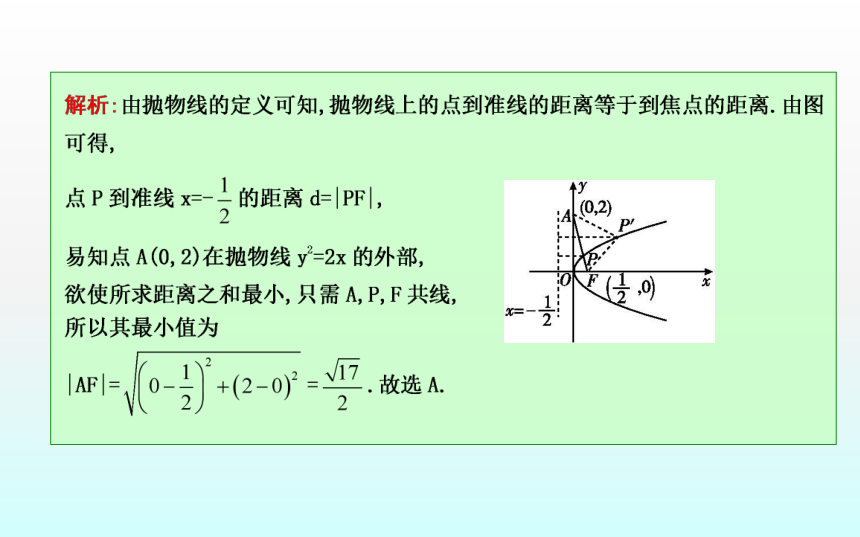
(2)解决与抛物线焦点、准线距离有关的最值、定值问题时,首先要注意应用抛物线的定义进行转化,其次是注意平面几何知识的应用,例如两点之间线段最短、三角形中三边间的不等关系、点与直线上点的连线中,垂线段最短等.解:(2)因为B( ,2)在抛物线的外部,
所以|PB|+d=|PB|+|PF|≥|BF|=2,
所以|PB|+d的最小值为2.(2)若B( ,2),求|PB|+d的最小值.题型二 抛物线的标准方程【例2】 分别求满足下列条件的抛物线的标准方程.
(1)以坐标轴为对称轴,且过点A(2,3);(2)以坐标轴为对称轴,焦点到准线的距离为 .方法技巧 求抛物线的标准方程的关键与方法
(1)关键:确定焦点在哪个坐标轴上,进而求方程的有关参数.
(2)方法:①直接法:建立恰当坐标系,利用抛物线的定义列出动点满足的条件,列出对应方程,化简方程;
②直接根据定义求p,最后写标准方程;
③利用待定系数法设标准方程,找有关的方程(组)求系数.即时训练2-1:根据下列条件,求抛物线的标准方程.
(1)准线为y=-1;
(2)焦点到准线的距离是4;解:(1)焦点在y轴正半轴上, =1,即p=2,
故抛物线的标准方程为x2=4y.
(2)p=4,故抛物线的标准方程有四种形式:
y2=8x,y2=-8x,x2=8y,x2=-8y.(3)过点(1,2).【备用例3】 根据条件求抛物线的标准方程.
抛物线的焦点是双曲线16x2-9y2=144的左顶点.题型三 抛物线的实际应用【例3】 如图是抛物线形拱桥,当水面在l时,拱顶离水面2 m,水面宽4 m.水位下降1 m后,求水面的宽度.题后反思 涉及与抛物线有关的桥的跨度,隧道高低等问题,一般用抛物线的标准方程来解决,建立直角坐标系后,应注意点坐标的正负及其实际意义.即时训练3-1:喷灌的喷头装在直立管柱OA的顶点A处,喷出水流的最高点B高5 m,且与OA所在的直线相距4 m,水流落在以O为圆心,半径为9 m的圆上,则管柱OA= m.?解析:如图所示,建立直角坐标系,设水流所形成的抛物线的方程为x2=
-2py(p>0),
因为点C(5,-5)在抛物线上,所以25=-2p·(-5),因此2p=5,
所以抛物线的方程为x2=-5y,
因为点A(-4,y0)在抛物线上,所以16=-5y0,即y0=- ,
所以OA的长为5- =1.8(m).即管柱OA的长为1.8 m.
答案:1.8谢谢观赏!
2.4.1 抛物线及其标准方程新知探求 素养养成知识点一梳理 抛物线的定义
平面内与一个定点F和一条定直线l(l不经过点F)距离 的点的轨迹叫做抛物线,点F叫做抛物线的 ,直线l叫做抛物线的 .相等焦点准线抛物线的定义知识点二梳理 抛物线标准方程的几种形式y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)题型一 抛物线定义的应用课堂探究 素养提升(2)是否存在M,使|MA|+|MF|取得最小值?若存在,求此时点M的坐标;若不存在,请说明理由.规范解答:(2)如图,由于点M在抛物线上,
所以|MF|等于点M到其准线l的距离|MN|,于是|MA|+|MF|=|MA|+|MN|,
…………………………………………………………………8分
所以当A,M,N三点共线时,|MA|+|MN|取最小值,亦即|MA|+|MF|取最小值,这时M的纵坐标为2,…………………………………………10分
分可设M(x0,2),代入抛物线方程得x0=2,即M(2,2).…………
………………………………………………………………12分方法技巧 (1)抛物线的定义中指明了抛物线上的点到焦点的距离与到准线的距离相等,故两者可相互转化,这也是利用抛物线定义解题的实质.
(2)解决与抛物线焦点、准线距离有关的最值、定值问题时,首先要注意应用抛物线的定义进行转化,其次是注意平面几何知识的应用,例如两点之间线段最短、三角形中三边间的不等关系、点与直线上点的连线中,垂线段最短等.解:(2)因为B( ,2)在抛物线的外部,
所以|PB|+d=|PB|+|PF|≥|BF|=2,
所以|PB|+d的最小值为2.(2)若B( ,2),求|PB|+d的最小值.题型二 抛物线的标准方程【例2】 分别求满足下列条件的抛物线的标准方程.
(1)以坐标轴为对称轴,且过点A(2,3);(2)以坐标轴为对称轴,焦点到准线的距离为 .方法技巧 求抛物线的标准方程的关键与方法
(1)关键:确定焦点在哪个坐标轴上,进而求方程的有关参数.
(2)方法:①直接法:建立恰当坐标系,利用抛物线的定义列出动点满足的条件,列出对应方程,化简方程;
②直接根据定义求p,最后写标准方程;
③利用待定系数法设标准方程,找有关的方程(组)求系数.即时训练2-1:根据下列条件,求抛物线的标准方程.
(1)准线为y=-1;
(2)焦点到准线的距离是4;解:(1)焦点在y轴正半轴上, =1,即p=2,
故抛物线的标准方程为x2=4y.
(2)p=4,故抛物线的标准方程有四种形式:
y2=8x,y2=-8x,x2=8y,x2=-8y.(3)过点(1,2).【备用例3】 根据条件求抛物线的标准方程.
抛物线的焦点是双曲线16x2-9y2=144的左顶点.题型三 抛物线的实际应用【例3】 如图是抛物线形拱桥,当水面在l时,拱顶离水面2 m,水面宽4 m.水位下降1 m后,求水面的宽度.题后反思 涉及与抛物线有关的桥的跨度,隧道高低等问题,一般用抛物线的标准方程来解决,建立直角坐标系后,应注意点坐标的正负及其实际意义.即时训练3-1:喷灌的喷头装在直立管柱OA的顶点A处,喷出水流的最高点B高5 m,且与OA所在的直线相距4 m,水流落在以O为圆心,半径为9 m的圆上,则管柱OA= m.?解析:如图所示,建立直角坐标系,设水流所形成的抛物线的方程为x2=
-2py(p>0),
因为点C(5,-5)在抛物线上,所以25=-2p·(-5),因此2p=5,
所以抛物线的方程为x2=-5y,
因为点A(-4,y0)在抛物线上,所以16=-5y0,即y0=- ,
所以OA的长为5- =1.8(m).即管柱OA的长为1.8 m.
答案:1.8谢谢观赏!
