人教新课标A版选修2-1第二章 圆锥曲线与方程2.4.2 抛物线的简单几何性质(28张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第二章 圆锥曲线与方程2.4.2 抛物线的简单几何性质(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览







文档简介
课件28张PPT。2.4.2 抛物线的简单几何性质新知探求 素养养成知识点问题:已知抛物线y2=8x,其图象如图所示.抛物线的简单几何性质(1)观察抛物线y2=8x图象可知其上的点的坐标的范围是怎样的?
答案:抛物线上的点的横坐标x≥0,纵坐标y∈R.
(2)观察抛物线y2=8x的图象有什么对称性?
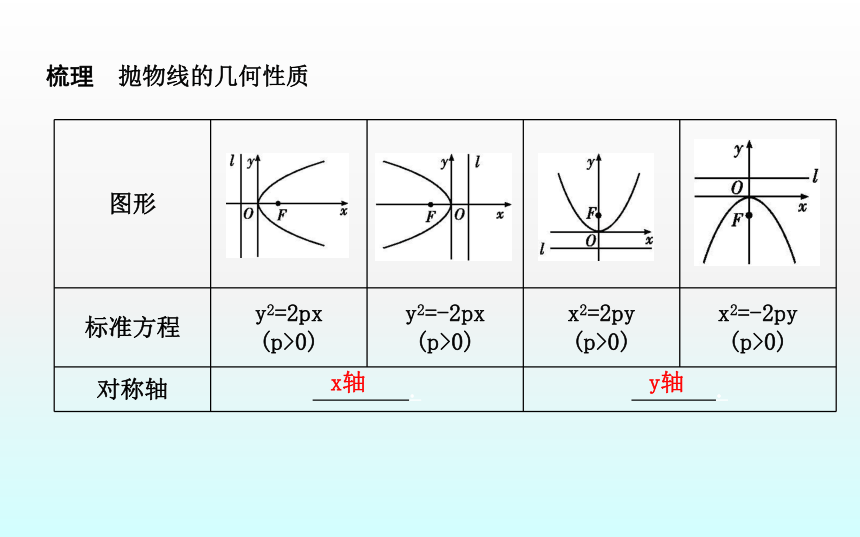
答案:关于x轴对称.梳理 抛物线的几何性质x轴y轴原点1名师点津:抛物线的焦点弦
如图,AB是过抛物线y2=2px(p>0)焦点F的一条弦,设 A(x1,y1),B(x2,y2),AB的中点M(x0,y0),相应的准线为l.
(1)以AB为直径的圆的圆心与准线l相切.
(2)|AB|=2(x0+ )(焦点弦长与中点关系).
(3)|AB|=x1+x2+p.
(4)若直线AB的倾斜角为α,则|AB|= .
如当α=90°时,AB叫做抛物线的通径,是所有焦点弦中最短的.
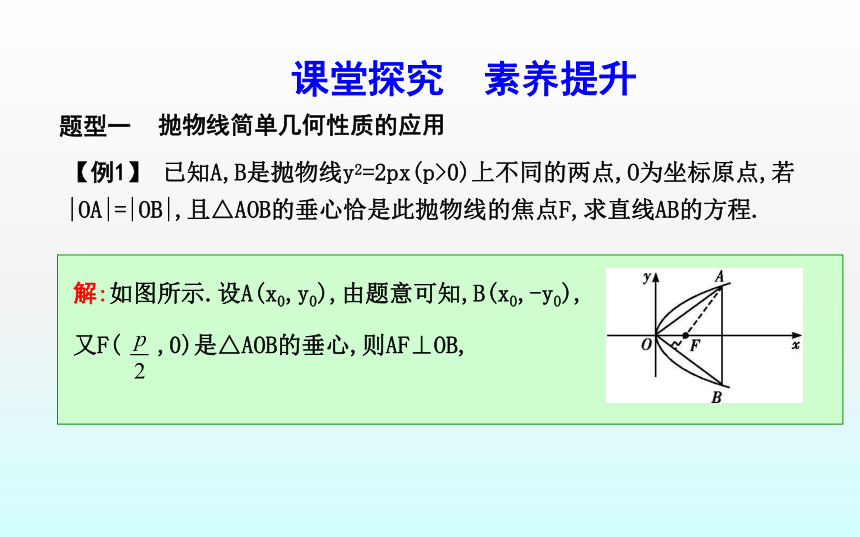
(5)A,B两点的横坐标之积、纵坐标之积为定值,即x1·x2= ,y1·y2=-p2.题型一 抛物线简单几何性质的应用课堂探究 素养提升【例1】 已知A,B是抛物线y2=2px(p>0)上不同的两点,O为坐标原点,若|OA|=|OB|,且△AOB的垂心恰是此抛物线的焦点F,求直线AB的方程.解:如图所示.设A(x0,y0),由题意可知,B(x0,-y0),
又F( ,0)是△AOB的垂心,则AF⊥OB,方法技巧 抛物线的几何性质(对称性、范围等)在解决抛物线问题时,有着广泛的应用,但在解题过程中又容易忽视这些隐含条件,如抛物线的对称性、准线与对称轴垂直等,解题时应注意挖掘并充分利用这些隐含条件.即时训练1-1:已知抛物线的焦点F在x轴上,直线l过F且垂直于x轴,l与抛物线交于A,B两点,O为坐标原点,若△OAB的面积等于4,求此抛物线的标准方程.【备用例1】 已知抛物线的顶点在坐标原点,对称轴为x轴,且与圆x2+y2=4相交于A,B两点,|AB|=2 ,求抛物线方程.解:由已知,抛物线的焦点可能在x轴正半轴上,也可能在负半轴上.
故可设抛物线方程为y2=ax(a≠0).
设抛物线与圆x2+y2=4的交点A(x1,y1),B(x2,y2).
因为抛物线y2=ax(a≠0)与圆x2+y2=4都关于x轴对称,
所以点A与B关于x轴对称,题型二 直线与抛物线的位置关系【例2】 已知直线l:y=k(x+1)与抛物线C:y2=4x.问:k为何值时,直线l与抛物线C有两个交点,一个交点,无交点?解:由方程组 消去y得
k2x2+(2k2-4)x+k2=0.
记Δ=(2k2-4)2-4k4=16(1-k2).
①若直线与抛物线有两个交点,
则k2≠0,且Δ>0,即k2≠0,且16(1-k2)>0,解得k∈(-1,0)∪(0,1).
所以当k∈(-1,0)∪(0,1)时,直线l和抛物线C有两个交点.②若直线与抛物线有一个交点,
则k2=0或k2≠0时,Δ=0.
解得k=0或k=±1.
所以当k=0或k=±1时,直线l和抛物线C有一个交点.
③若直线与抛物线无交点,
则k2≠0且Δ<0.
解得k>1或k<-1.
所以当k>1或k<-1时,直线l和抛物线C无交点.题后反思 研究直线和抛物线的位置关系时,由于消元后所得的方程中含参数,因此要注意分二次项系数为0和不为0两种情况讨论.即时训练2-1:(2018·乌鲁木齐高二期末)已知抛物线C:y2=2px(p>0)的焦点为F,M(3,2),直线MF交抛物线于A,B两点,且M为AB的中点,则p的值为( )
(A)3 (B)2或4
(C)4 (D)2题型三 抛物线的焦点弦问题【例3】 (10分)已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.若直线l的倾斜角为60°,求|AB|的值.一题多变:若本例中“直线l的倾斜角为60°”改为“|AB|=9”,求线段AB的中点M到准线的距离.方法技巧 求圆锥曲线的弦长时,为简化计算常常借助根与系数的关系,这样可以避免分别求x1,x2(或y1,y2)的麻烦,如果是利用弦长求参数的问题,只需要列出参数的方程或不等式即可求解,而x1,x2(或y1,y2)一般是求不出来的.【备用例2】 (2018·凌源市模拟)如图所示,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于两点A,B,交其准线l′于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
(A)y2=9x
(B)y2=6x
(C)y2=3x
(D)y2= x【例4】 已知点A(2,1)和抛物线C:y2=x,F为抛物线的焦点,P是C上任意一点.
(1)求|AP|+|PF|的最小值;题型四 抛物线中的最值问题(2)求点P到直线x+2y+4=0的距离的最小值.方法技巧 与抛物线上的点有关的最值问题,应注意抛物线上点的坐标的范围以及抛物线上点的坐标的设法(如y2=2px(p>0)中x≥0,y∈R,而抛物线上的点可设为(2pt2,2pt)或( ,y0)).即时训练4-1:抛物线y=4x2上一点到直线y=4x-5的距离最短,则该点的坐标是( )
(A)( ,1) (B)(0,0)
(C)(1,2) (D)(1,4)【备用例3】 已知抛物线C:y2=4x的焦点为F,过点F分别作两条直线l1,l2,直线l1与抛物线C交于A,B两点,直线l2与抛物线C交于D,E两点,若l1与l2的斜率的平方和为1,则|AB|+|DE|的最小值为( )
(A)16 (B)20 (C)24 (D)32谢谢观赏!
答案:抛物线上的点的横坐标x≥0,纵坐标y∈R.
(2)观察抛物线y2=8x的图象有什么对称性?
答案:关于x轴对称.梳理 抛物线的几何性质x轴y轴原点1名师点津:抛物线的焦点弦
如图,AB是过抛物线y2=2px(p>0)焦点F的一条弦,设 A(x1,y1),B(x2,y2),AB的中点M(x0,y0),相应的准线为l.
(1)以AB为直径的圆的圆心与准线l相切.
(2)|AB|=2(x0+ )(焦点弦长与中点关系).
(3)|AB|=x1+x2+p.
(4)若直线AB的倾斜角为α,则|AB|= .
如当α=90°时,AB叫做抛物线的通径,是所有焦点弦中最短的.
(5)A,B两点的横坐标之积、纵坐标之积为定值,即x1·x2= ,y1·y2=-p2.题型一 抛物线简单几何性质的应用课堂探究 素养提升【例1】 已知A,B是抛物线y2=2px(p>0)上不同的两点,O为坐标原点,若|OA|=|OB|,且△AOB的垂心恰是此抛物线的焦点F,求直线AB的方程.解:如图所示.设A(x0,y0),由题意可知,B(x0,-y0),
又F( ,0)是△AOB的垂心,则AF⊥OB,方法技巧 抛物线的几何性质(对称性、范围等)在解决抛物线问题时,有着广泛的应用,但在解题过程中又容易忽视这些隐含条件,如抛物线的对称性、准线与对称轴垂直等,解题时应注意挖掘并充分利用这些隐含条件.即时训练1-1:已知抛物线的焦点F在x轴上,直线l过F且垂直于x轴,l与抛物线交于A,B两点,O为坐标原点,若△OAB的面积等于4,求此抛物线的标准方程.【备用例1】 已知抛物线的顶点在坐标原点,对称轴为x轴,且与圆x2+y2=4相交于A,B两点,|AB|=2 ,求抛物线方程.解:由已知,抛物线的焦点可能在x轴正半轴上,也可能在负半轴上.
故可设抛物线方程为y2=ax(a≠0).
设抛物线与圆x2+y2=4的交点A(x1,y1),B(x2,y2).
因为抛物线y2=ax(a≠0)与圆x2+y2=4都关于x轴对称,
所以点A与B关于x轴对称,题型二 直线与抛物线的位置关系【例2】 已知直线l:y=k(x+1)与抛物线C:y2=4x.问:k为何值时,直线l与抛物线C有两个交点,一个交点,无交点?解:由方程组 消去y得
k2x2+(2k2-4)x+k2=0.
记Δ=(2k2-4)2-4k4=16(1-k2).
①若直线与抛物线有两个交点,
则k2≠0,且Δ>0,即k2≠0,且16(1-k2)>0,解得k∈(-1,0)∪(0,1).
所以当k∈(-1,0)∪(0,1)时,直线l和抛物线C有两个交点.②若直线与抛物线有一个交点,
则k2=0或k2≠0时,Δ=0.
解得k=0或k=±1.
所以当k=0或k=±1时,直线l和抛物线C有一个交点.
③若直线与抛物线无交点,
则k2≠0且Δ<0.
解得k>1或k<-1.
所以当k>1或k<-1时,直线l和抛物线C无交点.题后反思 研究直线和抛物线的位置关系时,由于消元后所得的方程中含参数,因此要注意分二次项系数为0和不为0两种情况讨论.即时训练2-1:(2018·乌鲁木齐高二期末)已知抛物线C:y2=2px(p>0)的焦点为F,M(3,2),直线MF交抛物线于A,B两点,且M为AB的中点,则p的值为( )
(A)3 (B)2或4
(C)4 (D)2题型三 抛物线的焦点弦问题【例3】 (10分)已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.若直线l的倾斜角为60°,求|AB|的值.一题多变:若本例中“直线l的倾斜角为60°”改为“|AB|=9”,求线段AB的中点M到准线的距离.方法技巧 求圆锥曲线的弦长时,为简化计算常常借助根与系数的关系,这样可以避免分别求x1,x2(或y1,y2)的麻烦,如果是利用弦长求参数的问题,只需要列出参数的方程或不等式即可求解,而x1,x2(或y1,y2)一般是求不出来的.【备用例2】 (2018·凌源市模拟)如图所示,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于两点A,B,交其准线l′于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
(A)y2=9x
(B)y2=6x
(C)y2=3x
(D)y2= x【例4】 已知点A(2,1)和抛物线C:y2=x,F为抛物线的焦点,P是C上任意一点.
(1)求|AP|+|PF|的最小值;题型四 抛物线中的最值问题(2)求点P到直线x+2y+4=0的距离的最小值.方法技巧 与抛物线上的点有关的最值问题,应注意抛物线上点的坐标的范围以及抛物线上点的坐标的设法(如y2=2px(p>0)中x≥0,y∈R,而抛物线上的点可设为(2pt2,2pt)或( ,y0)).即时训练4-1:抛物线y=4x2上一点到直线y=4x-5的距离最短,则该点的坐标是( )
(A)( ,1) (B)(0,0)
(C)(1,2) (D)(1,4)【备用例3】 已知抛物线C:y2=4x的焦点为F,过点F分别作两条直线l1,l2,直线l1与抛物线C交于A,B两点,直线l2与抛物线C交于D,E两点,若l1与l2的斜率的平方和为1,则|AB|+|DE|的最小值为( )
(A)16 (B)20 (C)24 (D)32谢谢观赏!
