人教新课标A版选修2-1第三章 空间向量与立体几何3.1.3 空间向量的数量积运算(32张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第三章 空间向量与立体几何3.1.3 空间向量的数量积运算(32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 16:00:43 | ||
图片预览











文档简介
课件32张PPT。3.1.3 空间向量的数量积运算新知探求 素养养成知识点一如图所示,已知平面向量a,b.
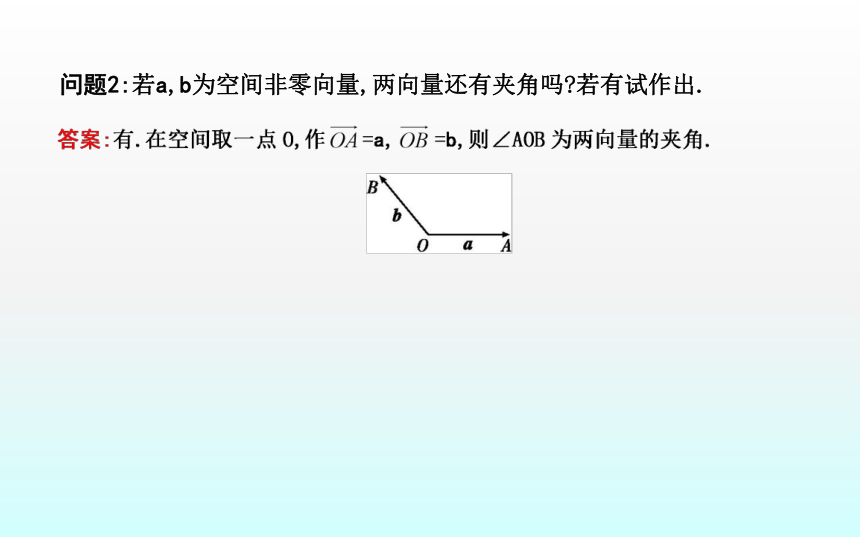
问题1:试作出向量a,b的夹角.空间向量的夹角答案:如图,∠AOB为a和b的夹角.问题2:若a,b为空间非零向量,两向量还有夹角吗?若有试作出.∠AOB(2)夹角的范围
空间任意两个向量的夹角θ的取值范围是 .特别地,当θ=0时,两向量同向共线;当θ=π时,两向量反向共线,所以若a∥b,则=0或π;当= 时,两向量垂直,记作a⊥b.[0,π] 知识点二空间向量的数量积问题3:平面向量中,(a·b)·c=a·(b·c)对吗?在空间向量中呢?
答案:不对,(a·b)·c表示一个与c共线的向量,而a·(b·c)表示一个与a共线的向量,c与a却不一定共线.在空间向量中也不对.
梳理 (1)定义:已知两个非零向量a,b,则 叫做a,b的数量积,记作a·b.|a||b|cos(2)数量积的运算律λ(a·b)b·aa·b+a·c(3)数量积的性质
①a,b是非零向量,则a⊥b ?a·b=0.④|a·b|≤|a||b|.题型一 空间向量数量积运算课堂探究 素养提升题型二 利用空间向量的数量积求夹角【例2】 已知BB1⊥平面ABC,且△ABC是∠B=90°的等腰直角三角形, ?ABB1A1,?BB1C1C的对角线都分别相互垂直且相等,若AB=a,求异面直线BA1与AC所成的角.方法技巧 (1)求几何体中两个向量的夹角可以把其中一个向量平移使其起点与另一个向量的起点重合,通过解三角形得出夹角的大小,此法就是求两个向量夹角的平移法.
(2)由两个向量的数量积定义得cos= ,求的大小,转化为求两个向量的数量积及两个向量的模的大小,求出的余弦值,进而求的大小.
(3)利用向量的数量积求出两向量的夹角,则这个夹角就是两异面直线所成的角或补角(注意异面直线所成角的范围).题型三 利用空间向量解决垂直问题【例3】 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB= ∠C1CD=∠BCD.求证:CA1⊥B1D1.方法技巧 用向量法证明垂直关系的操作步骤
(1)把几何问题转化为向量问题;(2)用已知向量表示所证向量;(3)结合数量积公式和运算律证明数量积为0;(4)将向量问题回归到几何问题.即时训练3-1:已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC. M,N分别是OA,BC的中点,G是MN的中点.求证:OG⊥BC.题型四 利用数量积求距离方法技巧 用空间向量求两点间距离,首先用其他已知夹角和模的向量表示此向量,再利用a·a=|a|2,通过向量运算求|a|.(2)若∠BAC=90°,∠BAA1=∠CAA1=60°,AB=AC=AA1=1,求MN的长.谢谢观赏!
问题1:试作出向量a,b的夹角.空间向量的夹角答案:如图,∠AOB为a和b的夹角.问题2:若a,b为空间非零向量,两向量还有夹角吗?若有试作出.∠AOB
空间任意两个向量的夹角θ的取值范围是 .特别地,当θ=0时,两向量同向共线;当θ=π时,两向量反向共线,所以若a∥b,则
答案:不对,(a·b)·c表示一个与c共线的向量,而a·(b·c)表示一个与a共线的向量,c与a却不一定共线.在空间向量中也不对.
梳理 (1)定义:已知两个非零向量a,b,则 叫做a,b的数量积,记作a·b.|a||b|cos
①a,b是非零向量,则a⊥b ?a·b=0.④|a·b|≤|a||b|.题型一 空间向量数量积运算课堂探究 素养提升题型二 利用空间向量的数量积求夹角【例2】 已知BB1⊥平面ABC,且△ABC是∠B=90°的等腰直角三角形, ?ABB1A1,?BB1C1C的对角线都分别相互垂直且相等,若AB=a,求异面直线BA1与AC所成的角.方法技巧 (1)求几何体中两个向量的夹角可以把其中一个向量平移使其起点与另一个向量的起点重合,通过解三角形得出夹角的大小,此法就是求两个向量夹角的平移法.
(2)由两个向量的数量积定义得cos
(3)利用向量的数量积求出两向量的夹角,则这个夹角就是两异面直线所成的角或补角(注意异面直线所成角的范围).题型三 利用空间向量解决垂直问题【例3】 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB= ∠C1CD=∠BCD.求证:CA1⊥B1D1.方法技巧 用向量法证明垂直关系的操作步骤
(1)把几何问题转化为向量问题;(2)用已知向量表示所证向量;(3)结合数量积公式和运算律证明数量积为0;(4)将向量问题回归到几何问题.即时训练3-1:已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC. M,N分别是OA,BC的中点,G是MN的中点.求证:OG⊥BC.题型四 利用数量积求距离方法技巧 用空间向量求两点间距离,首先用其他已知夹角和模的向量表示此向量,再利用a·a=|a|2,通过向量运算求|a|.(2)若∠BAC=90°,∠BAA1=∠CAA1=60°,AB=AC=AA1=1,求MN的长.谢谢观赏!
