人教新课标A版选修2-1第三章 空间向量与立体几何3.1.4 空间向量的正交分解及其坐标表示(23张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第三章 空间向量与立体几何3.1.4 空间向量的正交分解及其坐标表示(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 16:02:16 | ||
图片预览








文档简介
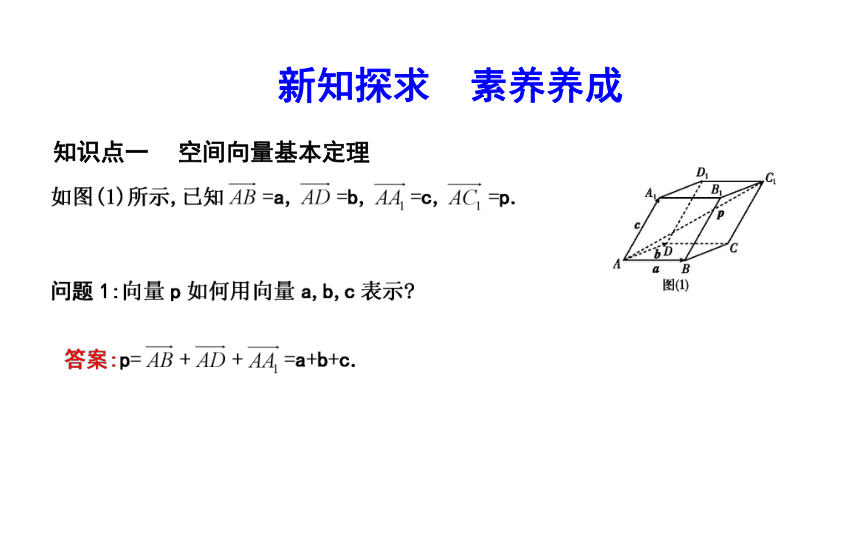
课件23张PPT。3.1.4 空间向量的正交分解及其坐标表示新知探求 素养养成知识点一空间向量基本定理梳理 如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p= .
其中{a,b,c}叫做空间的一个 ,a,b,c都叫做 .xa+yb+zc基底基向量知识点二空间向量的正交分解及其坐标表示如图(2)所示,已知正方体ABCD-A1B1C1D1的棱长为4,在AB,AD,AA1上分别取单位向量e1,e2,e3.梳理 (1)单位正交基底
有公共起点的三个 的单位向量e1,e2,e3称为单位正交基底.
(2)空间直角坐标系
以e1,e2,e3的公共起点O为原点,分别以e1,e2,e3的方向为x轴,y轴,z轴的正方向建立空间直角坐标系Oxyz.
(3)空间向量的坐标表示
对于空间任意一个向量p,一定可以把它平移,使它的起点与原点O重合,得到 向量=p.由空间向量基本定理可知,存在有序实数组{x,y,z}使得p=xe1+ye2+ze3.把x,y,z称作向量p在单位正交基底e1,e2,e3下的坐标,记作p= .两两垂直(x,y,z) 题型一 空间向量基本定理的理解课堂探究 素养提升【例1】 若{a,b,c}是空间一个基底,试判断{a+b,b+c,c+a}能否作为该空间的一个基底.解:假设a+b,b+c,c+a共面,
则存在实数λ,μ使得a+b=λ(b+c)+μ(c+a),
所以a+b=λb+μa+(λ+μ)c.
因为{a,b,c}为基底,所以a,b,c不共面.
所以 此方程组无解.所以a+b,b+c,c+a不共面,
所以{a+b,b+c,c+a}能作为空间的一个基底.一题多变:若本例条件不变,试判断{a+b,a-b,c}能否作为空间的一个基底.解:假设a+b,a-b,c共面,
则存在实数x,y,使c=x(a+b)+y(a-b),
即c=(x+y)a+(x-y)b,
从而由共面向量知c与a,b共面,
这与a,b,c不共面矛盾.
所以a+b,a-b,c不共面,即能作为空间的一个基底.方法技巧 判断某一向量组能否作为基底,关键是判断它们是否共面.如果从正面难以入手,可用反证法或利用一些常见的几何图形进行判断.题型二 空间向量基本定理的应用方法技巧 (1)若基底确定,要充分利用向量加法、减法的三角形法则和平行四边形法则,以及数乘向量的运算进行.
(2)若没给定基底,首先要选择基底,选择时,要尽量使所选的基向量能方便地表示其他向量,再就是看基向量的模及其夹角已知或易求.题型三 空间向量的坐标表示方法技巧 用坐标表示空间向量的方法步骤
(1)观察图形特征,寻找两两垂直的三条直线.
(2)根据图形特征建立空间直角坐标系.
(3)用基底表示向量.
(4)确定向量的坐标.谢谢观赏!
其中{a,b,c}叫做空间的一个 ,a,b,c都叫做 .xa+yb+zc基底基向量知识点二空间向量的正交分解及其坐标表示如图(2)所示,已知正方体ABCD-A1B1C1D1的棱长为4,在AB,AD,AA1上分别取单位向量e1,e2,e3.梳理 (1)单位正交基底
有公共起点的三个 的单位向量e1,e2,e3称为单位正交基底.
(2)空间直角坐标系
以e1,e2,e3的公共起点O为原点,分别以e1,e2,e3的方向为x轴,y轴,z轴的正方向建立空间直角坐标系Oxyz.
(3)空间向量的坐标表示
对于空间任意一个向量p,一定可以把它平移,使它的起点与原点O重合,得到 向量=p.由空间向量基本定理可知,存在有序实数组{x,y,z}使得p=xe1+ye2+ze3.把x,y,z称作向量p在单位正交基底e1,e2,e3下的坐标,记作p= .两两垂直(x,y,z) 题型一 空间向量基本定理的理解课堂探究 素养提升【例1】 若{a,b,c}是空间一个基底,试判断{a+b,b+c,c+a}能否作为该空间的一个基底.解:假设a+b,b+c,c+a共面,
则存在实数λ,μ使得a+b=λ(b+c)+μ(c+a),
所以a+b=λb+μa+(λ+μ)c.
因为{a,b,c}为基底,所以a,b,c不共面.
所以 此方程组无解.所以a+b,b+c,c+a不共面,
所以{a+b,b+c,c+a}能作为空间的一个基底.一题多变:若本例条件不变,试判断{a+b,a-b,c}能否作为空间的一个基底.解:假设a+b,a-b,c共面,
则存在实数x,y,使c=x(a+b)+y(a-b),
即c=(x+y)a+(x-y)b,
从而由共面向量知c与a,b共面,
这与a,b,c不共面矛盾.
所以a+b,a-b,c不共面,即能作为空间的一个基底.方法技巧 判断某一向量组能否作为基底,关键是判断它们是否共面.如果从正面难以入手,可用反证法或利用一些常见的几何图形进行判断.题型二 空间向量基本定理的应用方法技巧 (1)若基底确定,要充分利用向量加法、减法的三角形法则和平行四边形法则,以及数乘向量的运算进行.
(2)若没给定基底,首先要选择基底,选择时,要尽量使所选的基向量能方便地表示其他向量,再就是看基向量的模及其夹角已知或易求.题型三 空间向量的坐标表示方法技巧 用坐标表示空间向量的方法步骤
(1)观察图形特征,寻找两两垂直的三条直线.
(2)根据图形特征建立空间直角坐标系.
(3)用基底表示向量.
(4)确定向量的坐标.谢谢观赏!
